Virtual Lab Basic Experiment tutoriel - 4. Diffraction à fente unique

---

Préface

Cet article est le quatrième travail collectif de l'équipe dachuang,Expériences fondamentales sur l'optique physique–La Diffraction par fente unique et la diffraction par trou rectangulaire ont été explorées et essayées.

---

Un.、Introduction au principe expérimental de la diffraction à fente unique

1.Introduction à la diffraction

La Diffraction d'une seule fente est la lumière qui rencontre un obstacle dans sa propagation,Un phénomène dans lequel les ondes lumineuses continuent de se propager autour d'un obstacle.Si la longueur d'onde et la couture、Lorsque la taille du trou ou de l'obstacle est égale ou supérieure,Le phénomène de diffraction est le plus évident.
Diffraction de Fresnel：
En optique,La Diffraction de Fresnel se réfère à la Diffraction des ondes lumineuses dans la région proche du champ,C'est - à - dire l'écran et la perforation par diffraction d'une source lumineuse ou d'un dessin diffractif(Obstacles)La distance est limitée. Ni la source lumineuse ni l'écran lumineux ne sont loin de l'obstacle , Et aucune lentille n'est utilisée . La lumière n'est pas directionnelle , C'est - à - dire que le front d'onde n'est pas plat .
La Diffraction de Fraunhofer：
La source lumineuse et l'écran lumineux sont très éloignés des obstacles , La lumière incidente est alors parallèle , La surface de l'onde est plane , La lumière diffractive est également parallèle . Cette diffraction s'appelle la diffraction Fraunhofer .Au labo, Nous pouvons facilement transformer une onde lumineuse sphérique incidente en lumière directionnelle à l'aide d'une lentille , Les conditions dans lesquelles la Diffraction de Fraunhofer peut être facilement réalisée .
Apparemment., La Diffraction de Fresnel est courante , La Diffraction de Fraunhofer n'est qu'un cas particulier .

2.Analyse des demi - bandes

à un angle de diffraction donné $\theta$Moyenne,Si$BC$ Juste coupé en un nombre pair de demi - bandes ,Et$Q$ Les points ont des lignes sombres pour l'interférence d'annulation ;Si$BC$ Juste un nombre impair de demi - bandes , Une demi - bande restante ne peut pas être annulée ,Point$Q$ Rayures lumineuses pour éliminer la longueur sèche ;Si$BC$ Pas un multiple intégral d'une demi - longueur d'onde ,Et$Q$ La luminosité du point se situe entre le Sous - maximum et le minimum , Cela signifie également que chaque niveau de bande a une largeur correspondante .
En plus,Si$\theta$Plus l'angle est grand,Et$BC$Plus elle est longue., Donc plus il y a de demi - bandes , Et la largeur de la couture $AB$Constante, Donc la surface de chaque demi - bande doit être réduite （ C'est - à - dire que l'énergie lumineuse transportée sur chaque demi - bande diminue ）, Plus la série est élevée, , Plus la luminosité de la bande lumineuse est faible , Ça finit par devenir flou. . Ainsi, les ordres de diffraction observés sont également limités .

3.Formule

Conditions lumineuses $bsin\theta =\pm （2k+1）\frac{\lambda }{2}$
Conditions de texture foncée $bsin\theta =k\lambda$
Rayure centrale $-\lambda <bsin\theta <\lambda$, Largeur du coin $2{\theta }_0=2\frac{\lambda }{b}$,Largeur de ligne$\Delta x_0=2\frac{\lambda }{b}f$
La largeur des autres niveaux d'ombrage est l'espacement des ombres adjacentes. $\Delta x=\frac{\lambda f}{b}$, On peut voir que l'astigmatisme central est environ le double de la largeur des autres astigmatismes. .

4.Facteurs influant sur la diffraction

Plus la couture est étroite , Plus la diffraction est importante ,Mais...$b$Pas moins de$\lambda$($b$Moins de$\lambda$Heure, La théorie des demi - bandes n'est pas valable .）
Plus la couture est large , Moins la diffraction est évidente , La bande s'approche du Centre , Se déplace progressivement en ligne droite .
$\lambda$Plus grand., Plus le phénomène de diffraction est évident .
Quand la lumière blanche arrive , Le motif central reste blanc , Autres niveaux de violet à rouge ,Généralités$2,3$ Les niveaux commencent à se chevaucher .
Mouvement vers le haut et vers le bas d'une seule couture , Le diagramme de diffraction est inchangé selon le principe de l'imagerie par lentille . Déplacer légèrement la position de la couture unique vers le haut et vers le bas , Pas d'effet sur les franges diffractives ; Déplacer légèrement la position de la lentille vers le haut et vers le bas , .Alors toutes les franges se déplaceront aussi vers le haut et vers le bas , Mais l'espacement des bandes reste le même .

5.Diffraction des trous rectangulaires

$E(x,y)=C{\int }_{-\frac{a}{2}}^{\frac{a}{2}}exp(-i2\pi u{x}_1)d{x}_1{\int }_{-\frac{b}{2}}^{\frac{b}{2}}exp(-i2\pi v{y}_1)d{y}_1$
Note:： Son patron de diffraction est son patron de transformation de Fourier .
$=Cab\frac{sin\alpha }{\alpha }\ast \frac{sin\beta }{\beta }$
$u=\frac{x}{\lambda f},v=\frac{y}{\lambda f}$
$\alpha =\frac{\pi x}{\lambda f}a,\beta =\frac{\pi y}{\lambda f}b$

6.DiscussionYDistribution des bandes axiales

$I_y=I_0(\frac{sin\beta }{\beta }{)}^2$
Position du grand maître $\beta =0,I_{max}=I_0$
Emplacement du minimum $\beta =n\pi ,n=\pm 1,\pm 2$
C'est - à - dire:$y=\frac{n\lambda f}{b}$, Par conséquent, la largeur de la bande lumineuse centrale $Y=\frac{2\lambda f}{b}$, Position secondaire $\frac{d}{d\beta }\frac{sin\beta }{\beta }=0$
L'intervalle entre les lignes sombres ：$e=\frac{\lambda f}{b}$

2.、VirtualabSimulation

1.Construire des sentiers lumineux

Trouvez d'abord l'onde plane dans la bibliothèque et faites - la glisser dans le panneau ：

Double - cliquez pour définir les propriétés de l'onde plane ：
Régler la longueur d'onde à 632.8nmLa lumière rouge de, Et la forme de l'onde est rectangulaire ,La taille est110um×3mm（ La source d'onde est un peu plus grande que le trou ）：
PS： En fait, c'est plus grand que Kong. , Un peu plus grand, ça ira


Trouvé dans la Bibliothèque Aperture.

Glissez le trou derrière la source d'onde et définissez les paramètres du trou comme un trou rectangulaire 100um×3mm（ Parce que ce n'est pas une fente idéale , Il y a encore des limites à la longueur et à la largeur , C'est - à - dire un trou rectangulaire très étroit ）

Placer une lentille idéale infinie derrière ,La focale est100mm.

2.La clé du détecteur

Placer deux détecteurs au point focal de la lentille pour former une image bidimensionnelle et une image unidimensionnelle , La distance entre les deux détecteurs est réglée à 100mm（ Le détecteur est toujours dans le plan focal ）

（1） Configuration du détecteur 2D ：
Définir la taille de la fenêtre de la sonde à 20mm×2mm

Définir le réglage du point d'échantillonnage à user defined Et réglé à 2048×1024

Attention!： La méthode d'interpolation par défaut de la sonde est requise Cubic 6 PointLire comme suit:Accelerated Sinc
Sinon, les résultats de diffraction ne montrent que deux ordres .

（2） Configuration du détecteur unidimensionnel ：

Définir la taille de la fenêtre de la sonde à 20mm×10um

Définir le réglage du point d'échantillonnage à user defined Et réglé à 2048×1

Il est également nécessaire de modifier la méthode d'interpolation par défaut de la sonde Cubic 6 PointLire comme suit:Accelerated Sinc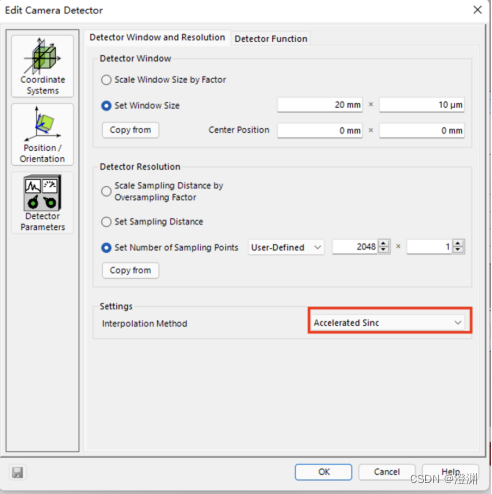

3.Finition des effets avec des traces classiques sur le terrain

La carte lumineuse construite est la suivante: ：

Comme tous les dispositifs utilisés sont idéaux ,Disponible enclassic field tracing

Obtenir une image unidimensionnelle bidimensionnelle ：


Jusqu'à présent, l'expérience de base est terminée. .

Trois、Présentation des résultats

Et puis..., Nous ajustons les paramètres , Observer le changement dynamique de la diffraction à fente unique .

1.Changer la focale

Tout d'abord,, Mettre la focale de 50mmÀ1000mChangement, La distance du détecteur doit être changée de façon synchrone .


Utiliserparameter run, Pour obtenir ces résultats expérimentaux après l'opération .

La formule donne , Lorsque les autres conditions sont inchangées , Augmentation de la focale , La largeur maximale du maître central augmente , Il y aura un grand élargissement du Centre , Phénomène de déplacement vers l'extérieur de la position de la ligne lumineuse secondaire .

2.Changer la longueur d'onde

Et voilà., Longueur d'onde de 400nmÀ700nmChangement.

Les résultats expérimentaux suivants ont été obtenus après l'opération .

C'est similaire à ce qui s'est passé lorsque la distance focale a été modifiée ci - dessus , Lorsque les autres conditions sont inchangées , Peut encore être dérivé de la formule , Lorsque la longueur d'onde augmente , Le phénomène de diffraction d'une seule fente est similaire , Le maître central s'élargit considérablement , Phénomène de déplacement vers l'extérieur de la position de la ligne lumineuse secondaire .

3.Changer la largeur de la couture

Même chose.,Nous utilisonsparameter runChanger la largeur de la couture（40um-115um）,Après l'opération, On peut obtenir de tels résultats de diffraction dynamique .

Lorsque les autres conditions sont inchangées , Peut être déduit de la formule , Augmentation de la largeur de la couture ,eRéduction, C'est - à - dire que la largeur maximale du maître central devient plus étroite , Rétrécissement maximal de l'hôte Central , Phénomène de déplacement interne de la position de la ligne lumineuse secondaire .

Oui.50um Largeur de la couture （Bleu）Et100um Largeur de la couture （Rouge） Les images sont combinées pour les comparer ,On peut le découvrir., La largeur maximale centrale de la ligne rouge est inférieure à celle de la Ligne bleue , En accord avec l'inférence théorique .

4.Déplacer la position d'une seule couture

Une seule couture （ Ouverture lumineuse ） Translation latérale dans l'espace aérien , Les résultats sont les suivants: ：

Déplacement latéral de l'ouverture de la lumière sur l'écran diffractif dans l'espace aérien , N'affecte pas la distribution d'amplitude de l'intensité de la diffraction Fraunhofer , Il y a juste un changement linéaire dans sa phase , La répartition de l'intensité lumineuse sur la surface d'acceptation reste inchangée .

5.Déplacer la position de la lentille

Lorsque la lentille se déplace latéralement dans l'espace aérien ,Les résultats sont présentés ci - dessous., La Ligne bleue est l'original. , La ligne rouge indique l'image après traduction .

Le déplacement de phase linéaire dans l'espace aérien provoque un déplacement latéral de la distribution du spectre , Lorsque l'ouverture ou l'écran diffractif est éclairé par un faisceau d'ondes planes inclinées d'amplitude unitaire , La distribution de l'intensité de Fraunhofer est translationnelle .

6.Construire une seule fente à l'aide d'une grille rectangulaire

En plus, Comment construire une fente parfaite .UtiliserRectangular Grating.

Régler la largeur de la couture , Aucun des paramètres de décalage ci - dessous n'affecte la position finale de la bande .

Remplacer une seule couture par cet élément , Modification et amélioration de la configuration originale de la carte routière lumineuse .

Et voilà., Importer la fonction de transmission que vous venez de créer .

Après l'opération,Les résultats sont les suivants:, L'effet est idéal , La largeur et l'emplacement des grands et des petits centres peuvent être bien observés .

7.Diffraction traditionnelle des trous rectangulaires

Si elle est réglée à la Diffraction des trous rectangulaires , Changer le paramètre de couture unique en

En même temps, Le paramètre d'éclairage doit également être supérieur à une seule fente .

Après l'opération, On peut obtenir de telles images de simulation expérimentale .

Annexe

Cet article est rédigé par les membres de l'équipe dachuang ： Tang yiheng 、 Aidez Yang Yu 、 Huang Yinuo 、 Li sitong 、 Ming Yue l'a fait ensemble. .
Cet article utilise une version d'essai largement disponible et 7.6.1.18 Version pour l'expérimentation et la démonstration ,Amélioration de l'applicabilité.
La Diffraction à fente unique est un exemple important de la théorie de la diffraction , Cet article est la Diffraction de Fraunhofer .