Balanced binary tree (AVL tree)

Balanced binary trees (AVL Trees )

Look at a case ( Explain the possible problem of binary sort tree )

I'll give you a sequence {1,2,3,4,5,6}, A binary sort tree is required (BST), And analyze the problem .
On the left BST Analysis of existing problems :

1. All left subtrees are empty , In form , It's more like a single linked list .
2. The insertion speed has no effect
3. The query speed is significantly reduced ( Because we need to compare ), Can't play BST The advantages of , Because every time you need to compare the left subtree , The query speed is faster than that Single linked list is slow
4. Solution - Balanced binary trees (AVL)

Basic introduction

1. Balanced binary tree is also called balanced binary search tree （Self-balancing binary search tree） Also known as AVL Trees , It can ensure high query efficiency .
2. It has the following characteristics ： It's one The absolute value of the height difference between an empty tree or its left and right subtrees shall not exceed 1, And both the left and right subtrees are one Balanced binary trees .
   The common way to realize balanced binary tree is red black tree 、AVL、 Scapegoat tree 、Treap、 Stretch the trees, etc .
3. Illustrate with examples , Take a look at the following AVL Trees , Why? ?
   

The application case - Single rotation ( Left rotation )

1. requirement : I'll give you a sequence , Create the corresponding balanced binary tree . The sequence {4,3,6,5,7,8} 2) Thought analysis ( Sketch Map )
   
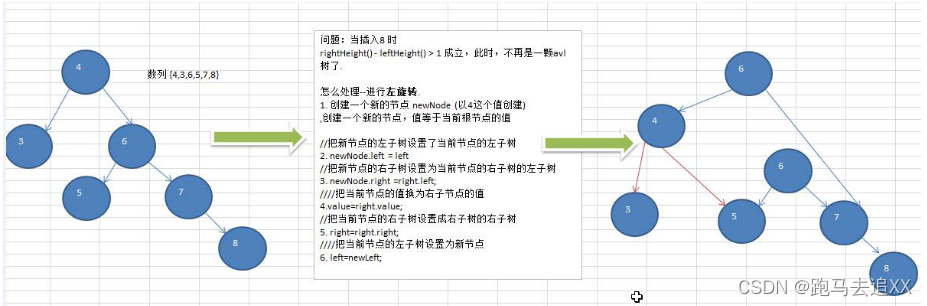
2. Code implementation

 public void leftRotate() {
    
        // Create a new node , With the value of the current root 
        Node newNode = new Node(value);
        // Set the new node's left subtree to the current node's left subtree 
        newNode.left = left;
        // Set the right subtree of the new node to the left subtree of the right subtree with your past nodes 
        newNode.right = right.left;
        // Replace the value of the current node with the value of the right child node 
        value = right.value;
        // Set the right subtree of the current node to the right subtree of the current node 
        right = right.right;
        // Put the left subtree of the current node ( Left child node ) Set to a new node 
        left = newNode;
    }

The application case - Single rotation ( Right rotation )

1. requirement : I'll give you a sequence , Create the corresponding balanced binary tree . The sequence {10,12, 8, 9, 7, 6}
2. Thought analysis ( Sketch Map )
   
3. Code implementation

 public void rightRotate() {
    
        Node newNode = new Node(value);
        newNode.right = right;
        newNode.left = left.right;
        value = left.value;
        left = left.left;
        right = newNode;
    }

The application case - Double rotation

The first two sequences , Make a single spin ( It's a rotation ) We can turn a non-equilibrium binary tree into a balanced binary tree , But in some cases , Single rotation Can't complete the transformation of balanced binary tree .
Like a sequence of numbers int[] arr = { 10, 11, 7, 6, 8, 9 }; Run the original code to see , It didn't turn into AVL Trees .
int[] arr = {2,1,6,5,7,3}; // Run the original code to see , It didn't turn into AVL Trees

1. Problem analysis
   
2. Solution analysis

1. When the symbol is rotated to the right
2. If the height of the right subtree of its left subtree is greater than the height of its left subtree
3. First, rotate the left node of the current node
4. Right rotate the current node

3. Code implementation [AVL Tree summary code ( Complete code )]

package com.iflytek.avl;

public class AVLTreeDemo {
    
  public static void main(String[] args) {
    
      int[] arr = {
    10, 11, 7, 6, 8, 9};
      // Create a  AVLTree  object 
      AVLTree avlTree = new AVLTree();
      // Add node 
      for (int i = 0; i < arr.length; i++) {
    
          avlTree.add(new Node(arr[i]));
      }
      // Traverse 
      System.out.println(" In the sequence traversal ");
      avlTree.infixOrder();
      System.out.println(" In balancing ~~");
      System.out.println(" The height of the tree =" + avlTree.getRoot().height()); //3
      System.out.println(" The height of the left subtree of the tree =" + avlTree.getRoot().leftHeight()); // 2
      System.out.println(" The height of the right subtree of the tree =" + avlTree.getRoot().rightHeight()); // 2
      System.out.println(" Current root =" + avlTree.getRoot());//8
  }
}

// establish AVLTree
class AVLTree {
    
  private Node root;

  public Node getRoot() {
    
      return root;
  }

  // Find the node to delete 
  public Node search(int value) {
    
      if (root == null) {
    
          return null;
      } else {
    
          return root.search(value);
      }
  }

  // Find the parent node 
  public Node searchParent(int value) {
    
      if (root == null) {
    
          return null;
      } else {
    
          return root.searchParent(value);
      }
  }
  //  Compiling method :
  // 1.  Back to   With  node  The value of the maximum node of the left subtree of the binary sort tree with root node 
  // 2.  Delete  node  The largest node of the left subtree of the binary sort tree with root node 

  /** * @param node  Incoming node ( As the root node of binary sort tree ) * @return  Back to   With  node  Is the value of the smallest node of the binary sort tree of the root node  */
  public int delLeftTreeMax(Node node) {
    
      Node target = node;
      //  Loop to find the right child node , You'll find the maximum 
      while (target.right != null) {
    
          target = target.right;
      }
      //  At this time  target  It points to the largest node 
      //  Delete maximum node 
      delNode(target.value);

      return target.value;
  }

  // Delete node 
  public void delNode(int value) {
    
      if (root == null) {
    
          return;
      } else {
    
          Node targetNode = search(value);
          //  If the node to be deleted is not found 
          if (targetNode == null) {
    
              return;
          }
          //  If we find that there is only one node in the current binary sorting tree 
          if (root.left == null && root.right == null) {
    
              root = null;
              return;
          }
          //  Go find  targetNode  The parent node 
          Node parent = searchParent(value);
          //  If the node to be deleted is a leaf node 
          if (targetNode.left == null && targetNode.right == null) {
    
              //  Judge  targetNode  Is the left child of the parent node , Or the right child node 
              if (parent.left != null && parent.left.value == value) {
    // It's the left child node 
                  parent.left = null;
              } else if (parent.right != null && parent.right.value == value) {
    // It's the right child node 
                  parent.right = null;

              }
          } else if (targetNode.left != null && targetNode.right != null) {
    //  Delete the node with two subtrees 
              int maxVal = delLeftTreeMax(targetNode.left);
              targetNode.value = maxVal;
          } else {
    //  Delete a node with only one subtree 
              //  If the node to be deleted has left child nodes 
              if (targetNode.left != null) {
    
                  if (parent != null) {
    
                      //  If  targetNode  yes  parent  Left child node of 
                      if (parent.left.value == value) {
    
                          parent.left = targetNode.left;
                      } else {
    
                          parent.right = targetNode.left;
                      }
                  } else {
    
                      root = targetNode.left;
                  }
              } else {
    //  If the node to be deleted has a right child 
                  if (parent != null) {
    
                      //  If  targetNode  yes  parent  Left child node of 
                      if (parent.left.value == value) {
    
                          parent.left = targetNode.right;
                      } else {
    
                          parent.right = targetNode.right;
                      }
                  } else {
    
                      root = targetNode.right;
                  }
              }
          }
      }
  }

  //  How to add nodes 
  public void add(Node node) {
    
      if (root == null) {
    
          root = node;
      } else {
    
          root.add(node);
      }
  }

  //  In the sequence traversal 
  public void infixOrder() {
    
      if (root != null) {
    
          root.infixOrder();
      } else {
    
          System.out.println(" Binary sort tree is empty , Can not traverse ");
      }
  }
}

// establish Node  node 
class Node {
    
  int value;
  Node left;
  Node right;

  public Node(int value) {
    
      this.value = value;
  }

  @Override
  public String toString() {
    
      return "Node{" +
              "value=" + value +
              '}';
  }

  //  return   The height of the tree with this node as the root 
  public int height() {
    
      return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
  }

  //  Return to the height of the right subtree 
  public int rightHeight() {
    
      if (right == null) {
    
          return 0;
      }
      return right.height();
  }

  public void leftRotate() {
    
      // Create a new node , With the value of the current root 
      Node newNode = new Node(value);
      // Set the new node's left subtree to the current node's left subtree 
      newNode.left = left;
      // Set the right subtree of the new node to the left subtree of the right subtree with your past nodes 
      newNode.right = right.left;
      // Replace the value of the current node with the value of the right child node 
      value = right.value;
      // Set the right subtree of the current node to the right subtree of the current node 
      right = right.right;
      // Put the left subtree of the current node ( Left child node ) Set to a new node 
      left = newNode;
  }

  public void rightRotate() {
    
      Node newNode = new Node(value);
      newNode.right = right;
      newNode.left = left.right;
      value = left.value;
      left = left.left;
      right = newNode;
  }

  //  Return to the height of the left subtree 
  public int leftHeight() {
    
      if (left == null) {
    
          return 0;
      }
      return left.height();
  }
  // Find the node to delete 

  /** * @param value  The value you want to delete  * @return  If found, return the node , Otherwise return to  null */
  public Node search(int value) {
    
      if (this.value == value) {
    
          return this;
      } else if (value < this.value) {
    
          if (this.left == null) {
    
              return null;
          }
          return this.left.search(value);
      } else {
    
          if (this.right == null) {
    
              return null;
          }
          return this.right.search(value);
      }
  }
  // Find the parent of the node you want to delete 

  /** * @param value  The value of the node to find  * @return  Return the parent of the node to be deleted , If not, go back  null */
  public Node searchParent(int value) {
    
      // If the current node is the parent of the node to be deleted , Just go back to 
      // The program is executed from left to right , You must first judge that the child node is not empty , Then the values can be compared 
      if ((this.left != null && this.left.value == value) ||
              (this.right != null && this.right.value == value)) {
    
          return this;
      } else {
    
          // If the search value is less than the value of the current node ,  And the left child of the current node is not empty 
          if (this.value > value && this.left != null) {
    
              return this.left.searchParent(value);// Search left subtree recursively 
          } else if (this.value <= value && this.right != null) {
    
              return this.right.searchParent(value);// Search right subtree recursively 
          } else {
    
              return null;//  No parent found 
          }
      }
  }

  // How to add nodes 
  //  Add nodes recursively , Note that the binary sort tree needs to be satisfied 
  public void add(Node node) {
    
      if (node == null) {
    
          return;
      }
      // Determine the value of the incoming node , The value relationship with the root node of the current subtree 
      if (node.value < this.value) {
    // The value of the added node is less than   The value of the current node 
          // If the left child of the current node is  null
          if (this.left == null) {
    
              this.left = node;
          } else {
    
              // Recursively add... To the left subtree 
              this.left.add(node);
          }
      } else {
    // The value of the added node is greater than   The value of the current node 
          if (this.right == null) {
    
              this.right = node;
          } else {
    
              // Recursively add... To the right subtree 
              this.right.add(node);
          }
      }
      // After adding a node , If : ( The height of the right subtree - The height of the left subtree ) > 1 ,  Left rotation 
      if (rightHeight() - leftHeight() > 1) {
    
          // If the height of the left subtree of its right subtree is greater than the height of its right subtree 
          if (right != null && right.leftHeight() > right.rightHeight()) {
    
              // First, rotate the right child node to the right 
              right.rightRotate();
              // Then rotate the current node to the left 
              leftRotate();// Left rotation ..
          } else {
    
              // Just rotate it to the left 
              leftRotate();
          }
          return;// It has to be !!!
      }
      // After adding a node , If  ( The height of the left subtree  -  The height of the right subtree ) > 1,  Right rotation 
      if (leftHeight() - rightHeight() > 1) {
    
          // If the height of the right subtree of its left subtree is greater than the height of its left subtree 
          if (left != null && left.rightHeight() > left.leftHeight()) {
    
              // First, for the left node of the current node ( The left subtree )-> Left rotation 
              left.leftRotate();
              // Then rotate the current node to the right 
              rightRotate();
          } else {
    
              // Just rotate right 
              rightRotate();
          }
      }
  }

  public void infixOrder() {
    
      if (this.left != null) {
    
          this.left.infixOrder();
      }
      System.out.println(this);
      if (this.right != null) {
    
          this.right.infixOrder();
      }
  }
}