Machine learning series (5): Naive Bayes

Naive Bayes Naive Bayes It is a classification method based on Bayesian theorem and characteristic hypothesis .

For a given set of training data , First, we assume that the learning input is independent based on the feature conditions / Joint distribution of outputs ; And then based on this model , For given x, Using Bayes theorem to get the output with the maximum posterior probability y.

Naive Bayes is easy to implement , The efficiency of learning and forecasting is very high , Is a common method .

One 、 Learning and classification of naive Bayes

1.1 Bayes theorem

Let's first look at what is conditional probability

P(A|B) Indicates an event B On the premise that it has happened , event A Probability of occurrence , It's called an event B What happened A Conditional probability of occurrence , The basic solution formula is ：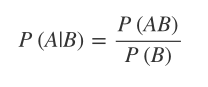

Bayes fixed 理 Is based on conditional probability , adopt P(A|B) Come and ask for P(B|A)：

incidentally 便 Mention it , The denominator in the above formula , It can be decomposed into

1.2 Independent hypothesis of characteristic conditions

This part begins with the naive Bayes 理 On derivation , From it you will deeply understand 什 What is the characteristic conditional independence hypothesis .

Given the training data set （X,Y）, Each of these samples X It all includes n Whitman's sign , namely x=(x₁,x₂,…,x_n), The class tag collection contains K Species category , namely y=(y₁,y₂,…,y_k)

If you come now 了 A new sample x How do we judge its category ? From a probabilistic point of view , The problem is given x, The probability of which category it belongs to 更 Big . Then the problem will be solved P(y₁|x),P(y₂|x),P(y_k|x) The biggest one , That is, find the output with the maximum a posteriori probability ：$argmax$_YkP(y_k|x)

that P(y_k|x) How to solve it ？ The answer is the Bayes theorem ：

According to the full probability formula , The denominator in the above formula can be further decomposed :
First 不 Tube denominator , In molecules P(y_k) It's a priori probability , According to the training set, it can be simply calculated , And conditional probability P(x|y_k)=p(x₁,x₂,…,x_n|y_k), Its parameter scale is exponential 量 Grade , Hypothesis number 1 i Whitman's sign x_i The number of values that can be taken is S_i individual , The number of class values is k individual , Then the number of parameters is $k\Pi$ⁿ_j=1S_j

This is obviously 不 can 行 Of . In response to this question , Naive Bayesian algorithm makes the assumption of independence for conditional probability distribution , Generally speaking, it means to assume the characteristics of each dimension x₁,x₂,…,x_n Independent to each other , Because this is a strong assumption , Hence the name of naive Bayesian algorithm . On the premise of this assumption , Conditional probability can be transformed into ：

In this way, the parameter scale is reduced to $\sum$ⁿ_i=1S_ik

The above is the assumption of characteristic conditional independence for conditional probability , thus , Prior probability P(y_k) And conditional probability P(x|y_k) All the problems will be solved 了, So we are 不 It can solve the posterior probability we need P(y_k|x)了.

The answer is yes . Let's continue with the above about P(y_k|x) The derivation of , The formula 2 Generation into the formula 1 Get in

So naive Bayes classification 器 Can be expressed as :

Because for all the y_k, The denominator values in the above formula are the same （ Why? ？ Note that the full plus sign allows 易理 Explain 了）, So you can suddenly 略 Denominator part , Naive Bayes split period is finally expressed as ：

Two 、 Parameter estimation of naive Bayesian method

2.1 Maximum likelihood estimation

Based on the above , What naive Bayes needs to learn is P(Y=c_k) and P(X^j=a_jl|Y=c_k) , The maximum likelihood estimation method can be used to estimate the corresponding probability （ In short , Is to use samples to infer the parameters of the model , Or the parameter that maximizes the likelihood function ）.

Prior probability P(Y=c_k) The maximum likelihood estimate of is

That is to say, use the sample c_k The number of occurrences divided by the sample size .

Derivation process

Set the first j Features x^(j) The set of possible values is a_j1,a_j2,…,a_jl, Conditional probability *P(X^j=a_jl|Y=c_k)* The maximum likelihood estimate of is
In style ,x^(j)_i It's No i Of samples j Features .

Example

2.2 Bayesian estimation

There is a hidden danger in maximum likelihood estimation , What if there is no combination of parameters and categories in the training data ？ For example, go to 例 When in Y=1 Corresponding X⁽¹⁾ The value of is only 1 and 2 . In this way, the probability value to be estimated may be 0 The situation of , But this 不 There is no such combination in real data . This will affect the calculation result of posterior probability , Make the classification deviate . The solution is Bayesian estimation .

Bayesian estimation of conditional probability

among λ≥0,S_j Express x_j The median of possible values . The numerator and denominator are more than the maximum likelihood estimation respectively 了 A little bit , Its meaning is in random change 量 Assign a positive number to the frequency of each value λ≥0. When λ=0 Is the maximum likelihood estimation ,λ Constant access 1, This is called Laplacian smoothing .

Bayesian estimation of a priori probability

Example

3、 ... and 、python Code implementation

3.1 Naive Bayesian document classification

from numpy import *
class Naive_Bayes:
    def __init__(self):
        self._creteria = "NB"
    #  establish 不 Repeated word set 
    def _creatVocabList(self,dataSet):
        vocabSet = set([]) #  Create an empty  SET
        for document in dataSet:
            vocabSet = vocabSet | set(document) #  Combine 
        return list(vocabSet) #  No return 不 Repeat the word list （ SET  Characteristics of ）
    #  Document word set to 量 Model 
    def _setOfWordToVec(self,vocabList, inputSet):
        """  function : Given ⼀ Line direction 量inputSet, Map it to ⾄ To the thesaurus 量vocabList, If it appears, it is marked as 1, Otherwise, mark   by 0. """
        returnVec = [0] * len(vocabList)
        for word in inputSet:
            if word in vocabList:
                returnVec[vocabList.index(word)] = 1
        return returnVec
    # ⽂ Document bag model 
    def _bagOfsetOfWordToVec(self,vocabList, inputSet):
        """  function ： For each 行 Word use the second statistical strategy 略, Count the number of single words , Then map to this library   Output ： One n Dimensionality 量,n Is the length of the thesaurus , Each value is the number of occurrences of the word  """
        returnVec = [0] * len(vocabList)
        for word in inputSet:
            if word in vocabList:
                 returnVec[vocabList.index(word)] += 1 # 更 New here code 
        return returnVec
    def _trainNB0(self,trainMatrix, trainCategory):
        """  transport ⼊ Enter into ： Training word matrix trainMatrix And category labels trainCategory, The format is Numpy Matrix format   function ： Calculate the conditional probability p0Vect、p1Vect And class label probability pAbusive """
        numTrainDocs = len(trainMatrix)#  Number of samples 
        numWords = len(trainMatrix[0])#  The number of features , Here is the Thesaurus ⻓ length 
        pAbusive = sum(trainCategory) / float(numTrainDocs)#  Calculate the probability of negative samples （ Prior probability ）
        p0Num = ones(numWords)#  The number of occurrences of the initial word is  1 , In case the conditional probability is  0 , Affect the outcome 
        p1Num = ones(numWords)#  ditto 
        p0Denom = 2.0#  Class is marked with  2 , Use Laplacian smoothing  ,
        p1Denom = 2.0
        #  Mark in by class 行 Aggregate each word direction 量
        for i in range(numTrainDocs):
            if trainCategory[i] == 0:
                p0Num += trainMatrix[i]
                p0Denom += sum(trainMatrix[i])
            else:
                p1Num += trainMatrix[i]
                p1Denom += sum(trainMatrix[i])
        p1Vect = log(p1Num / p1Denom)#  Calculate under the given class tag , The probability of a word appearing in the thesaurus 
        p0Vect = log(p0Num / p0Denom)#  take  log  logarithm , Prevent the conditional probability product from being too small ⽽ And underflow occurs 
        return p0Vect, p1Vect, pAbusive
    def _classifyNB(self,vec2Classify, p0Vec, p1Vec, pClass1):
        '''  The algorithm contains four inputs ⼊ Enter into : vec2Classify Represents the mapping set of the samples to be classified in the thesaurus , p0Vec The conditional probability P(wi|c=0)P(wi|c=0), p1Vec The conditional probability P(wi|c=1)P(wi|c=1), pClass1 Indicates that the class label is 1 The probability of time P(c=1)P(c=1). p1=ln[p(w1|c=1)p(w2|c=1)…p(wn|c=1)p(c=1)] p0=ln[p(w1|c=0)p(w2|c=0)…p(wn|c=0)p(c=0)] log Take logarithm to prevent downward overflow   function : Using naive Bayes 行 classification , The return result is 0/1 '''
        p1 = sum(vec2Classify * p1Vec) + log(pClass1)
        p0 = sum(vec2Classify * p0Vec) + log(1 - pClass1)
        if p1 > p0:
            return 1
        else:
            return 0
    #test
    def testingNB(self,testSample):
        #"step1： Load datasets and class labels "
        listOPosts, listClasses = loadDataSet()
        #"step2： Create a Thesaurus "
        vocabList = self._creatVocabList(listOPosts)
        #"step3： Calculate the occurrence of each sample in the thesaurus "
        trainMat = []
        for postinDoc in listOPosts:
            trainMat.append(self._bagOfsetOfWordToVec(vocabList, postinDoc))
        p0V, p1V, pAb = self._trainNB0(trainMat, listClasses)
        # "step4： test "
        thisDoc = array(self._bagOfsetOfWordToVec(vocabList, testSample))
        result=self._classifyNB(thisDoc, p0V, p1V, pAb)
        print('classified as:%d'%(result))
        # return result
#################################
#  Load data set 
def loadDataSet():
    postingList = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'
                ],
                ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0, 1, 0, 1, 0, 1] # 1 is abusive, 0 not
    return postingList, classVec
#  test 
if __name__=="__main__":
    clf = Naive_Bayes()
    testEntry = [['love', 'my', 'girl', 'friend'],
    ['stupid', 'garbage'],
    ['Haha', 'I', 'really', "Love", "You"],
    ['This', 'is', "my", "dog"],
    ['maybe','stupid','worthless']]
    for item in testEntry:
        clf.testingNB(item)

3.2 Use naive Bayes to filter spam

import re
from numpy import *
# mysent='This book is the best book on Python or M.L I have ever laid eyes upon.'
# regEx = re.compile('\\W*')
# listOfTokens=regEx.split(mysent)
# tok=[tok.upper() for tok in listOfTokens if len(tok)>0]
# print tok
#
# emailText=open('email/ham/6.txt').read()
# listOfTokens=regEx.split(emailText)
# print listOfTokens
def textParse(bigString):
    import re
    listOfTokens=re.split(r'\w*',bigString)
    return [tok.lower() for tok in listOfTokens if len(tok)>2]
def spamTest():
    clf = Naive_Bayes()
    docList=[]
    classList=[]
    fullText=[]
    for i in range(1,26):
        wordList=textParse(open('email/spam/%d.txt'%i).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(1)
        wordList=textParse(open('email/ham/%i.txt'%i).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(0)
    vocabList=clf._creatVocabList(docList)
    trainingSet=range(50);testSet=[]
    for i in range(10):
        randIndex=int(random.uniform(0,len(trainingSet)))
        testSet.append(trainingSet[randIndex])
        del(trainingSet[randIndex])
    trainMatix=[];trainClasses=[]
    for docIndex in trainingSet:
        trainMatix.append(clf._bagOfsetOfWordToVec(vocabList,docList[docIndex]))
        trainClasses.append(classList[docIndex])
    p0V,p1V,pSpam=clf._trainNB0(array(trainMatix),array(trainClasses))
    errorCount = 0
    for docIndex in testSet:
        wordVector = clf._bagOfsetOfWordToVec(vocabList,docList[docIndex])
        if clf._classifyNB(array(wordVector), p0V, p1V, pSpam)!=classList[docIndex]:
            errorCount+=1
    print('the error rate is :%f'%(float(errorCount)/len(testSet)))
    spamTest()

Machine combat source code and data
link ：https://pan.baidu.com/s/163rCxsqepQqXSiK4qlTizw .
Extraction code ：fyny