当前位置：网站首页>朴素贝叶斯分类

朴素贝叶斯分类

2022-07-30 02:58:00 【Caaaaaan】

分类概念

  • 分类：找出描述和区别数据类或概念的模型，以便能够使用模型预测类标号未知的对象的类标号
  • 一般过程：
    • 学习阶段
      • 建立描述预先定义的数据类或概念集的分类器
      • 训练集提供了每个训练元组的类标号，分类的学习过程也成为监督学习
    • 分类阶段
      • 使用定义好的分类器进行分类的过程

概念区分：

  1. 分类与预测
    • 分类是预测分类（离散、无序）标号
    • 预测建立连续值函数模型，来预测一个数值
  2. 分类与聚类
    • 分类是有监督学习，提供了训练元组的类标号
    • 聚类是无监督学习，不依赖有类标号的训练实例

朴素贝叶斯分类

介绍

  • 一种后验概率：是事先观察不到的一个概率值

P ( h ∣ D ) = P ( D ∣ h ) P ( h ) P ( D ) P ( h ∣ D ) 表示在 D 的情况下， h 的概率是多少 P(h|D)=\frac{P(D|h)P(h)}{P(D)}\\ P(h|D)表示在D的情况下，h的概率是多少 P(h∣D)=P(D)P(D∣h)P(h)​P(h∣D)表示在D的情况下，h的概率是多少

在这里插入图片描述

定义分类器

定义： P ( h ∣ D ) = P ( D ∣ h ) P ( h ) P ( D ) P ( h ∣ D ) : h 的后验概率 P ( D ∣ h ) : h 的似然概率 − 从训练集中已知 P ( h ) : h 的先验概率 P ( D ) : D 的先验概率 D : 待测试数据 h : 假设类别 定义：\\ P(h|D)=\frac{P(D|h)P(h)}{P(D)}\\ P(h|D):h的后验概率\\ P(D|h):h的似然概率-从训练集中已知\\ P(h):h的先验概率\\ P(D):D的先验概率\\ D:待测试数据\\ h:假设类别\\ 定义：P(h∣D)=P(D)P(D∣h)P(h)​P(h∣D):h的后验概率P(D∣h):h的似然概率−从训练集中已知P(h):h的先验概率P(D):D的先验概率D:待测试数据h:假设类别

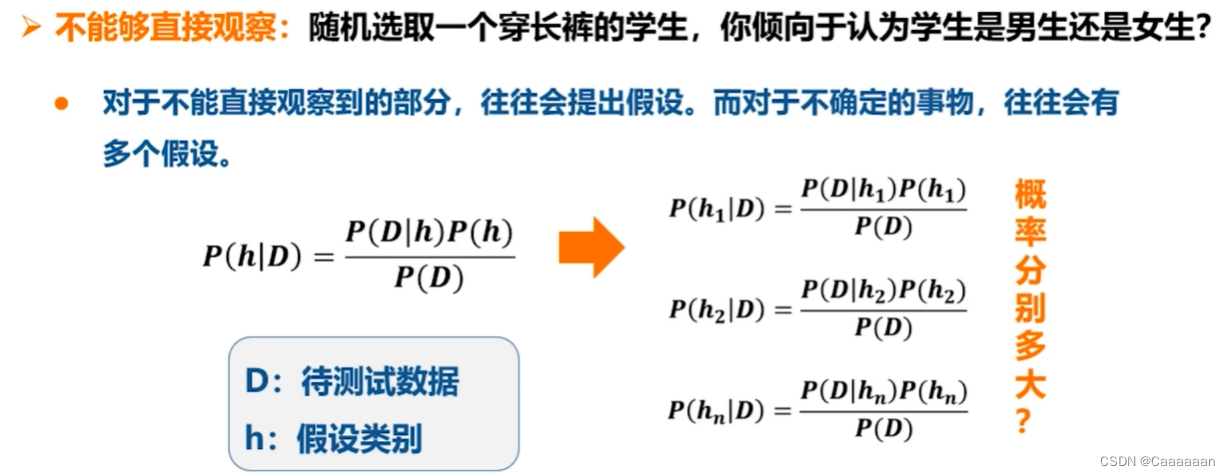
在这里插入图片描述

我们对其提出多个假设——h1,h2,h3…

哪个概率更大，我们就认为D属于哪个类别更合理

  • 极大后验假设定义

    学习器在候选假设集合H中寻找给定数据D时可能性最大的假设h，h被称为极大后验假设

P ( h 1 ∣ D ) = P ( D ∣ h 1 ) P ( h 1 ) P ( D ) P ( h 2 ∣ D ) = P ( D ∣ h 2 ) P ( h 2 ) P ( D ) P ( h 3 ∣ D ) = P ( D ∣ h 3 ) P ( h 3 ) P ( D ) h M A P = max ⁡ h ∈ H P ( h ∣ D ) = max ⁡ h ∈ H P ( D ∣ h ) P ( h ) P ( D ) = max ⁡ h ∈ H P ( D ∣ h ) P ( h ) P(h_1|D)=\frac{P(D|h_1)P(h_1)}{P(D)}\\ P(h_2|D)=\frac{P(D|h_2)P(h_2)}{P(D)}\\ P(h_3|D)=\frac{P(D|h_3)P(h_3)}{P(D)}\\ h_{MAP}=\max_{h\in H}P(h|D)\\ =\max_{h\in H}\frac{P(D|h)P(h)}{P(D)}\\ =\max_{h\in H}P(D|h)P(h) P(h1​∣D)=P(D)P(D∣h1​)P(h1​)​P(h2​∣D)=P(D)P(D∣h2​)P(h2​)​P(h3​∣D)=P(D)P(D∣h3​)P(h3​)​hMAP​=h∈Hmax​P(h∣D)=h∈Hmax​P(D)P(D∣h)P(h)​=h∈Hmax​P(D∣h)P(h)

  • 对象D是一个多维向量

    eg:一个收入中等，信用度良好的青年爱好游戏顾客，是否会购买电脑

    从中可以得到4个维度特征，即该对象时4维向量

  • 多维对象——联合概率

∙ 已知：对象 D 是由多个属性组成的向量 ( 向量维度根据特征数目 ) D = < a 1 , a 2 , . . . , a n > ∙ 目标： h M A P = max ⁡ h ∈ H P ( h ∣ D ) h M A P = max ⁡ h ∈ H P ( h ∣ < a 1 , a 2 , . . . , a n > ) max ⁡ h ∈ H P ( < a 1 , a 2 , . . . , a n > ∣ h ) P ( h ) \bullet已知：对象D是由多个属性组成的向量(向量维度根据特征数目)\\ D=<a_1,a_2,...,a_n>\\ \bullet目标：h_{MAP}=\max_{h\in H}P(h|D)\\ h_{MAP}=\max_{h\in H}P(h|<a_1,a_2,...,a_n>)\\ \max_{h\in H}P(<a_1,a_2,...,a_n>|h)P(h)\\ ∙已知：对象D是由多个属性组成的向量(向量维度根据特征数目)D=<a1​,a2​,...,an​>∙目标：hMAP​=h∈Hmax​P(h∣D)hMAP​=h∈Hmax​P(h∣<a1​,a2​,...,an​>)h∈Hmax​P(<a1​,a2​,...,an​>∣h)P(h)

  • 问题：当维度过高时，可用数据会变得很稀疏，难以获得结果

  • 对于联合概率的极大开销，我们提出一个假设

    假设每个属性都是独立同分布的

    在独立同分布的假设下，我们的联合概率变成各个属性条件概率的连乘

∙ 假设 D 的属性 a i 之间相互独立 P ( < a 1 , a 2 , . . . , a n > ∣ h ) = ∏ i n P ( a i ∣ h ) h M A P = max ⁡ h ∈ H P ( h ∣ < a 1 , a 2 , . . . , a n > ) = max ⁡ h ∈ H P ( < a 1 , a 2 , . . . , a n > ∣ h ) P ( h ) = max ⁡ h ∈ H ∏ i n P ( a i ∣ h ) p ( h ) \bullet 假设D的属性a_i之间相互独立\\ P(<a_1,a_2,...,a_n>|h)=\prod_i^nP(a_i|h)\\ h_{MAP}=\max_{h\in H}P(h|<a_1,a_2,...,a_n>)\\ =\max_{h\in H}P(<a_1,a_2,...,a_n>|h)P(h)\\ =\max_{h\in H}\prod_i^nP(a_i|h)p(h) ∙假设D的属性ai​之间相互独立P(<a1​,a2​,...,an​>∣h)=i∏n​P(ai​∣h)hMAP​=h∈Hmax​P(h∣<a1​,a2​,...,an​>)=h∈Hmax​P(<a1​,a2​,...,an​>∣h)P(h)=h∈Hmax​i∏n​P(ai​∣h)p(h)

  • 优点:
    • 降低计算开销
    • 如果D的属性之间不满足相互独立(即存在一定的相关性)，我们就可以使用相关性计算减少属性再使用朴素贝叶斯，朴素贝叶斯分类的结果是贝叶斯分类的近似

朴素贝叶斯分类案例

得到相应的似然概率

在这里插入图片描述

在购买电脑的情况(这个就是假设h)下：

  • 青年的似然概率
  • 收入中等的似然概率
  • 爱好的似然概率
  • 信用值为中的似然概率

即得到 测试对象对应属性的 在测试集中 在假设h下的似然概率

在这里插入图片描述

似然概率*先验概率=后验概率

在这里插入图片描述

则得出结论，该顾客更有可能购买计算机

连续数据解决概率

问题：当数据是连续的时候，我们很难通过计数统计，得出相应的概率

方法一：数据离散化

  • 等宽法、等频法、聚类等方法，将其离散化

方法二：假设正态分布，采用密度函数进行计算似然概率

  • ！！！注意，似然概率计算之后要乘以先验概率

在上述例子中，收入是{高、中、低}离散化的

若收入变成连续数值

  1. 假设不同类别收入分别服从不同的正态分布

    在这个例子中表现为，在购买和不购买两个类别中，收入这个数值服从不一样的正态分布

P ( X i ∣ c j ) = 1 2 π σ i j 2 e − ( x i − μ i j ) 2 2 σ i j 2 P(X_i|c_j)=\frac{1}{\sqrt{2\pi\sigma_{ij}^2}}e^{-\frac{(x_i-\mu_{ij})^2}{2\sigma_{ij}^2}}\\ P(Xi​∣cj​)=2πσij2​​1​e−2σij2​(xi​−μij​)2​

  1. 利用参数估计n组正态分布期望和方差

    这个n取决于最终是多少个类别

    期望为 μ \mu μ，方差为 σ 2 \sigma^2 σ2

在这里插入图片描述

总结

  • 本质上是同时考虑了先验概率和似然概率的重要性
  • 特点
    • 属性可以离散，也可以连续
    • 数学基础坚实，分类效率稳定
    • 对缺失和噪声数据不太敏感
    • 属性不相关情况下，分类效果很好
原网站

版权声明
本文为[Caaaaaan]所创，转载请带上原文链接，感谢
https://blog.csdn.net/Hacker_ccc/article/details/126004585

边栏推荐

猜你喜欢

随机推荐