62. 不同路径

题目

62. 不同路径

难度

中等。

描述

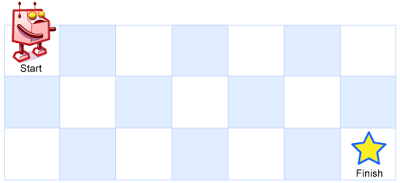
假设有一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

例如，上图是一个 7 x 3 的网格。有多少可能的路径？

示例 1:

输入: m = 3, n = 2

输出: 3

解释:

从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向右 -> 向下

2. 向右 -> 向下 -> 向右

3. 向下 -> 向右 -> 向右
   示例 2:

输入: m = 7, n = 3

输出: 28

解答

解题思路

采用动态规划的方法，主要分三步走：

1. 定义数组元素含义： 首先定义 dp[i][j] 是机器人从左上角走到 (i, j) 时，那么就共有 dp[i][j] 种方案；
2. 找到关系数组元素间的关系式： 其次，如果要到达 (i, j) 位置，主要有两种方法。第一种是从 (i - 1, j) 走一步就到，另一种是从 (i, j - 1) 走一步到达，因此关系是为两种情况相加：dp[i][j] = dp[i - 1][j] + dp[i][j - 1]；
3. 找出初始值： 最后一定不要忘了初始值即边界条件，当我们在最上面一行或者最左边一列时，此时都只有一种方案，我们就将其值初始化为 1；

代码实现

public int uniquePaths(int m, int n) {
    

    if(m <= 0 || n <= 0){
    
        return 0;
    }

    int[][] dp = new int[m][n];

    // 边界情况，初始值
    // 1. 最上方
    for(int i = 0; i < m; i++){
    
        dp[i][0] = 1;
    }

    // 2. 最左方
    for(int i = 0; i < n; i++){
    
        dp[0][i] = 1;
    }

    // 元素间的关系
    for(int i = 1; i < m; i++){
    
        for(int j = 1; j < n; j++){
    
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }

    return dp[m - 1][n - 1];
}

时间复杂度

主要是双层循环，所以复杂度是 O(m * n)，其中 m 和 n 分别是棋盘的长和宽。