当前位置:网站首页>[binary search] 4 Find the median of two positive arrays
[binary search] 4 Find the median of two positive arrays
2022-06-26 10:14:00 【Magic siege lion MRL】
4. Find the median of two positive arrays ( It's difficult )
Title Description
Given two sizes, they are m and n Positive order of ( From small to large ) Array nums1 and nums2. Please find and return the values of these two positive ordered arrays Median . The time complexity of the algorithm should be O(log (m+n)) .
Example 1:
Input :nums1 = [1,3], nums2 = [2]
Output :2.00000
explain : Merge array = [1,2,3] , Median 2
Example 2:
Input :nums1 = [1,2], nums2 = [3,4]
Output :2.50000
explain : Merge array = [1,2,3,4] , Median (2 + 3) / 2 = 2.5
Topic analysis
The median is an element in an ordered array that can divide all elements equally ,
If the array elements are odd , The element that happens to be in the middle ;
If the array elements are even , Is the middle 2 The mean of the elements ;
This topic gives two ordered arrays , Find the median of two ordered arrays after merging .
1、 Merge two ordered arrays
A natural idea is : Merge two ordered arrays into an ordered array , Then we can find the median by calculating the middle position through the subscript of the ordered array . The algorithm needs to traverse two ordered arrays , Its time complexity and space complexity are O(m+n).
Although you can submit this question , But the time complexity does not meet the requirements of the topic .
/* The median is an element in an ordered array that can divide all elements equally ,
If the array elements are odd , The element that happens to be in the middle ;
If the array elements are even , Is the middle 2 The mean of the elements ;
A natural idea is : Merge two ordered arrays into an ordered array , Then calculate the middle position through the subscript of the ordered array
The idea of the algorithm is O(m+n)*/
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int m=nums1.size();
int n=nums2.size();
int len=m+n;
vector<int> res(len);
int i=0,j=0,k=0;
while(i<m&&j<n){
if(nums1[i]<=nums2[j]) res[k++]=nums1[i++];
else res[k++]=nums2[j++];
}
while(i<m) res[k++]=nums1[i++];
while(j<n) res[k++]=nums2[j++];
if(len%2!=0) return (double)res[len/2.0];
else{
double mean=(res[len/2.0]+res[len/2.0-1])/2.0;
return mean;
}
}In the above code , We discuss the case of finding the median :
If the array elements are odd , The element that happens to be in the middle ;
If the array elements are even , Is the middle 2 The mean of the elements ;
To simplify the code , We can use a little trick :
Find the second (len+1) / 2 And (len+2) / 2 The value of the elements , Then find the average value , This applies to odd and even numbers .
If len For an odd number , So in fact (len+1) / 2 and (len+2) / 2 The values are equal , It's equivalent to adding two identical numbers and dividing by 2, Or itself .
The code implementation is also very simple :
// A technique for unifying the median
int left=(len+1)/2;
int right=(len+2)/2;
// Find the... From two ordered arrays left And the first right Large number
double mean=(res[left-1]+res[right-1])/2.0;
return mean;So our code can be modified to :
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int m=nums1.size();
int n=nums2.size();
int len=m+n;
vector<int> res(len);
int i=0,j=0,k=0;
while(i<m&&j<n){
if(nums1[i]<=nums2[j]) res[k++]=nums1[i++];
else res[k++]=nums2[j++];
}
while(i<m) res[k++]=nums1[i++];
while(j<n) res[k++]=nums2[j++];
// A technique for unifying the median
int left=(len+1)/2;
int right=(len+2)/2;
// Find the... From two ordered arrays left And the first right Large number
double mean=(res[left-1]+res[right-1])/2.0;
return mean;
}2、 Two points search
The time complexity of the algorithm should be O(log (m+n)), Obviously, this is the time complexity of binary search algorithm . Obviously we already know how to find the median in an array , Write it out first. :
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int m = nums1.size();
int n = nums2.size();
// Where you want to find
int left=(m+n+1)/2;
int right=(m+n+2)/2;
// Find the... From two ordered arrays left And the first right Large number
double mean=(findKth(nums1,nums2,0,0,left)+findKth(nums1,nums2,0,0, right))/2.0;
return mean;
}The key now is how to find the second in two ordered arrays k A large number , Set to findKth().
Define the meaning of this function as :
// from nums1 Of [i:] and nums2[j:] Of the two Ordered interval Search for The first k Big Number of numbers
int findKth(vector<int>& nums1, vector<int>& nums2,int i, int j, int k)
Reduce the size of the problem as you eliminate it in your search , It is obvious to find the second order from two ordered intervals 1 It's easy to get the answer when you count them :
if(k==1) return min(nums1[i], nums2[j]);// Find the first 1 Elements , Go straight back to
In scaling down the problem , If an ordered interval no longer exists , namely i>=nums1.size() perhaps j>=nums2.size() when , Finding the median will also be easier :
if(i>=nums1.size()) return nums2[j+k-1];//nums1 Empty array , Directly from nums2 In looking for
if(j>=nums2.size()) return nums1[i+k-1];//nums2 Empty array , Directly from nums1 In looking for
The difficulty lies in how to deal with the general situation ? Because we need to find the... In two ordered arrays K Elements .
To speed up the search , We need to use dichotomy , Yes K Two points , It means we need to separate in nums1 and nums2 Find the second K/2 Elements , Note here that because the length of the two arrays is uncertain , So it's possible that an array has no number K/2 A digital , So we need to check , Whether there is a second in the array K/2 A digital , If it exists, take it out , Otherwise, assign the last integer maximum value
If an array has no number K/2 A digital , So let's eliminate the top of another number K/2 Just a number . Is it possible that both arrays do not exist K/2 It's a number , It's impossible in this problem , Because of our K Not given arbitrarily , It's for you m+n The middle value of , So there must be at least one array K/2 A number of . Finally, it is the core of dichotomy , Compare the second... Of these two arrays K/2 Small numbers midVal1 and midVal2 Size , If the... Of the first array K/2 If the number is small , So the number we're looking for is definitely not nums1 In front of K/2 A digital , So we can eliminate it , take nums1 Move the starting position of the back K/2 individual , And now K Also subtract from K/2, Call recursion . conversely , We eliminate nums2 In front of K/2 A digital , And will nums2 Move the starting position of the back K/2 individual , And now K Also subtract from K/2, Call recursion .
// from nums1 Of [i:] and nums2[j:] To find the second order interval k Large number
int findKth(vector<int>& nums1, vector<int>& nums2,int i, int j, int k){
// Termination conditions
if(i>=nums1.size()) return nums2[j+k-1];//nums1 Empty array , Directly from nums2 In looking for
if(j>=nums2.size()) return nums1[i+k-1];//nums2 Empty array , Directly from nums1 In looking for
if(k==1) return min(nums1[i], nums2[j]);// Find the first 1 Elements , Go straight back to
// lookup nums1 No k/2 Big element , If it does not exist, it is set to infinity
int midVal1=(i+k/2-1<nums1.size())? nums1[i+k/2-1] : INT_MAX;
// lookup nums2 No k/2 Big element , If it does not exist, it is set to infinity
int midVal2=(j+k/2-1<nums2.size())? nums2[j+k/2-1] : INT_MAX;
// If midVal1<midVal2, It means that the median is definitely not nums1 Before k/2 Number
if(midVal1<midVal2) return findKth(nums1, nums2, i+k/2,j, k-k/2);
// If midVal1>=midVal2, It means that the median is definitely not nums2 Before k/2 Number
else return findKth(nums1, nums2, i,j+k/2 , k-k/2);
}边栏推荐
- The third-party extension package of thinkphp6.0 supports uploading to Alibaba cloud and qiniu cloud
- 2. merge two ordered arrays
- Tensorflow dynamically allocates video memory
- leetCode-链表的中间结点
- Automated testing -- Introduction and example of pytest framework
- DAY 3 数组,前置后置,字符空间,关键词和地址指针
- MySQL learning summary
- 【深度优先搜索】312.戳气球
- 首批12家企业入驻!广州首个集中展销老字号产品专柜开张
- Teach you to use shell script to check whether the server program is running
猜你喜欢

Detailed explanation of winsorflow quantum installation process

904. fruit baskets
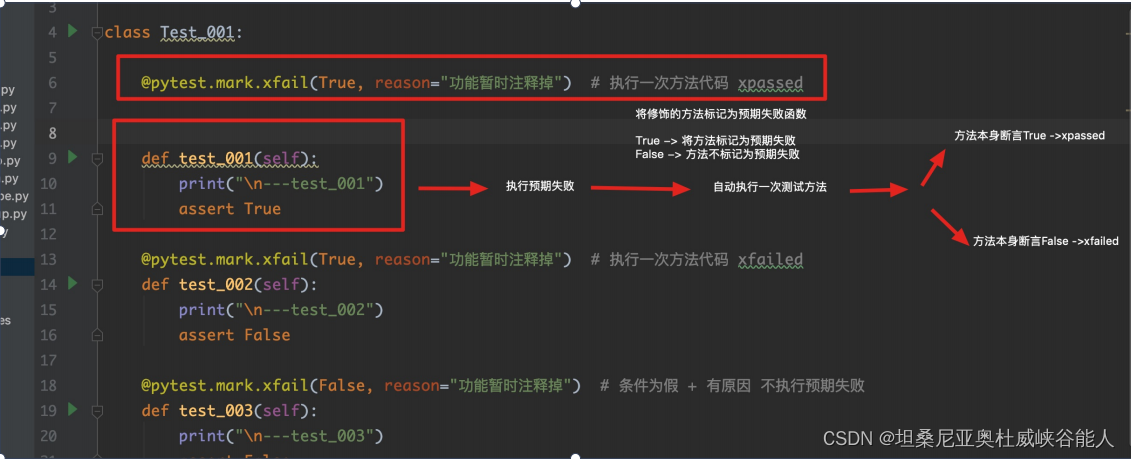
Automated testing -- Introduction and use of pytest itself and third-party modules

jar版本冲突问题解决
【Leetcode】76. Minimum covering substring

C中字符串基本操作

MySQL learning summary

DAY 3 数组,前置后置,字符空间,关键词和地址指针

方法区里面有什么——class文件、class文件常量池、运行时常量池

Test instructions - common interface protocol analysis
随机推荐
Download MySQL database installation package website of each system and version
Retrofit common request methods and comments, post, get heard file upload
什么是僵尸网络
118. Yanghui triangle
Daily-used English phrases
Allocation de mémoire tas lors de la création d'objets
c语言语法基础之——函数嵌套、递归 小程序斐波那契之和、阶乘
全渠道、多场景、跨平台,App如何借助数据分析渠道流量
自动化测试——pytest框架介绍及示例
WIN10系统实现Redis主从复制
The basis of C language grammar -- pointer (multidimensional array, function, summary) learning
Tensorflow dynamically allocates video memory
Software testing - how to select the appropriate orthogonal table
SQL advanced tutorial
存储过程测试入门案例
Automated testing -- Introduction and use of pytest itself and third-party modules
爬虫相关文章收藏:pyppeteer 、Burpsuite
In the fragment, the input method is hidden after clicking the confirm cancel button in the alertdialog (this is valid after looking for it on the Internet for a long time)
瑞萨电子面向物联网应用推出完整的智能传感器解决方案
1. sum of two numbers (leetcode topic)