On the improvement of 3dsc by harmonic shape context feature HSC

In the last blog post ( On the contextual features of three-dimensional shapes 3DSC Theory and Application ), We've already introduced it 3DSC Design principle and implementation details of , And this feature is limited by the defect of normal estimation to some extent . in fact , In the literature [1] in , The author is proposing 3DSC At the same time , The corresponding solutions are also given , To relieve 3DSC The inherent defects of , That is, harmonic shape contextual features Harmonic shape contexts(HSC). Today we will learn about HSC The principle and implementation of .

---

One . brief introduction

in the light of HSC The simplest and most direct explanation , to 3DSC Information is transformed in frequency domain . Due to the error of normal estimation in point cloud data , The local spherical spatial positioning with some points will cause anomalies . So give 3DSC Feature extraction brings unstable factors . According to the characteristics of point cloud , Except in the boundary area , Otherwise, the normal distribution of the point cloud should be continuous , Or normal transformation is smooth . that , For non boundary areas ,3DSC The corresponding histogram data changes should also be smooth . If a significant disturbance or data anomaly occurs in the non boundary region , Then it can be assumed that there is a problem with the normal estimation of the region . therefore , An intuitive solution is to use a frequency domain analysis to reduce the statistical information anomalies caused by random disturbances . Based on this idea ,HSC Proposed .

be based on 3DSC Create a histogram ,HSC Take it as a sample , For sphere shell( I don't know the exact translation , Combined with the context , Feeling is aimed at one bin The spherical cavity space of ), Calculate a spherical harmonic transformation .HSC The descriptor can be considered as the amplitude of the harmonic transformation , It has rotation invariance to azimuth , Therefore, the degrees of freedom associated with azimuth can be removed . below , Let's start the introduction HSC Specific steps of operator extraction .

---

Two . HSC Operator extraction

Any equation can be expressed as the sum of a set of spherical harmonic basis functions ( This is similar to the generalization of Fourier transform in three dimensions , That is, any function can not be expressed as a combination of trigonometric functions ). The summation is treated as a harmonic transformation f, Expressed mathematically as ：

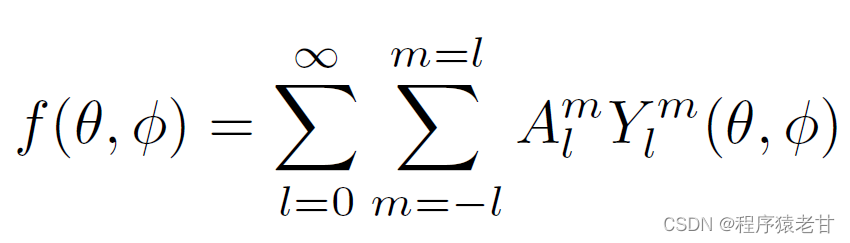
Y_l^m For the basis function mentioned earlier . An important feature of the transform is that the rotation transform according to azimuth is transformed into a phase transform in frequency domain . Harmonic coefficient ||A_l^m|| It is not affected by the change of direction angle . Based on pairwise harmonic transformation f The definition of , combination 3DSC Of bin data , Give an example of shell Function of fi, The definition is as follows ：

In frequency domain ,j The direction angle transformation represented is regarded as the displacement influenced by the independent signal . Such as Literature [2] Mentioned , Set a bandwidth here b, And only the... In the harmonic representation is stored b Low frequency part , Add to HSC, It is calculated as follows ：

For any real function , ||A_l^m||=||A_l^-m||, When m Less than 0 when , Discard factor ||A_l^m||. This is what we got HSC Dimension for Kb(b+1)/2. Be careful , The division of azimuth and potential difference does not affect HSC Dimensions ( I understand that K And b It is already information in frequency domain , It has nothing to do with the division of spatial data ).HSC And rotation invariant descriptor SH[2] relevant . The difference is ,SH Is used to describe global shape features . by comparison ,HSC The amplitudes of the individual frequency domain components are preserved , Therefore, the feature description is more detailed .

chart 1 A schematic diagram is given , To visualize HSC Rotation invariant property of . among , The pink area of the right subgraph represents a shell Area , When we calculate the frequency domain data of this region , Select different normals , You'll get different SC expression , Just like the red signal of the left subgraph , The distribution of data will shift . however , From the perspective of frequency domain , This shift in the time domain does not affect the data representation in the frequency domain . Two seemingly different time domain signals , After Fourier transform , Get exactly the same frequency domain expression . therefore , Established in the frequency domain HSC It has rotation invariance .

  chart 1. HSC Two dimensional schematic diagram of frequency domain features .

By distributing the data of spatial points , Signal representation converted to frequency domain ,HSC To a certain extent solved 3DSC Random perturbation problem of . Feature representation in frequency domain , Better robustness to rotation , More embodiment of each shell The speed of data distribution transformation , Not the data distribution itself . therefore , Obtained by harmonic transformation , Based on frequency domain signal representation HSC, To a certain extent solved 3DSC Rotation sensitive issues .

---

summary

HSC For resolution 3DSC Affected by normal estimation , Problems sensitive to rotation . By changing the information corresponding to the phase angle , Mapping to the corresponding frequency domain , Get the phase information in the frequency domain , Furthermore, a feature representation that is robust to rotation is obtained . But I think HSC For rotation Sensitive Solutions , Some are not satisfactory . The frequency domain transformation has actually caused the loss of information , What's more, we have to cut in the frequency domain . I haven't found it yet HSC Implementation code , in the light of HSC There is really very little information . This explains... From the side HSC In practice there is no such thing as 3DSC Bring about essential improvement . however ,HSC The ideas provided are worth learning , Try to solve the rotation problem in the frequency domain , There are still some things to do .

---

Reference

[1] A. Frome, et al. Recognizing objects in range data using regional point descriptors [C]. ECCV, 2004: 224-237.

[2] K. M, et al. Rotation invariant spherical harmonic representation of 3d shape descriptors. ACM SIGGRAPH symposium on Geometry processing, 2003:156-164.