当前位置:网站首页>Advanced mathematics | proficient in mean value theorem problem solving routines summary
Advanced mathematics | proficient in mean value theorem problem solving routines summary
2022-06-25 02:37:00 【Xipi yo】
Problem solving routine summary
Routine one


![]()

![]()
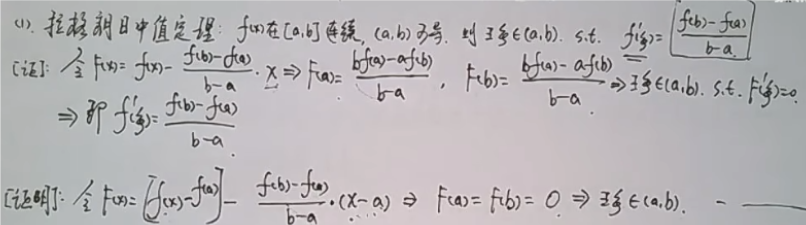

notes : In Cauchy mean value theorem g‘(x)≠0 Two denominators are limited at the same time You can use the counter evidence + Rolle

![]()







![]()

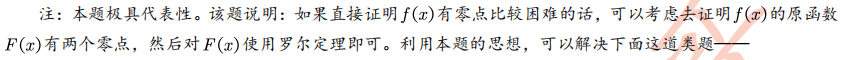
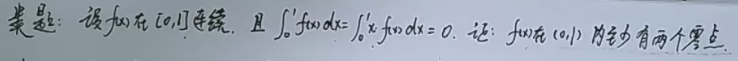

![]()

The root obtained from Rolle's theorem must be a single root .

Routine two Auxiliary polynomial
【 notes 】 structure
Purpose , It mainly refers to those in the question stem “ uneven ” The function value and derivative value of are all “ Zeroing ”, Thus making
Be able to use Rolle's theorem constantly , Greatly simplifies the problem !
【 notes 】 When setting a function , If zero is known , give an example , For example, quadratic function : Set to
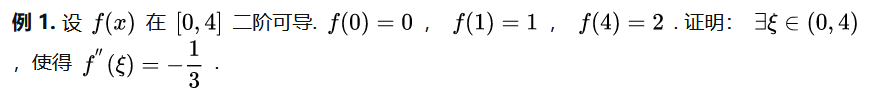



【 notes 】 Reviewing the problem-solving process of auxiliary polynomials, we know , because
yes n Sub polynomial , And we end up with auxiliary functions
Continuously find n Secondary derivative , So we get
, So the real impact 、 To determine the final conclusion , Only
The coefficient of the highest order term in ! As for those lower order terms, they all disappear in the process of derivation .
( Of course , This does not mean that the coefficients of the lower order terms can be written casually , Because only
When each coefficient in is accurate ,
There are so many zeros and stagnation points , It is possible to satisfy the conditions for the use of Rolle's theorem , You can't just because the coefficients of those lower order terms don't affect
, You think they're useless , Tool man is also a man ~)





【 notes 】 Special note , In this question
and
Although there are the same minimum values
, But the abscissa of their minimum values is not necessarily the same . So we need Classification of discussion . This idea can be applied to 2007 In the postgraduate entrance examination in !


【 notes 】
As mentioned above , When using auxiliary polynomials to solve problems , If the conclusion is
, You need to construct a
Polynomial fitting . because n Polynomial of degree has
A coefficient of , So the question is in the stem Only
When there are two independent conditions , Then all the coefficients in the auxiliary function cannot be solved smoothly .
To solve this problem , We need to give
“ Impose constraints ”, Make the constructed
Can solve the problem smoothly .
As for what conditions need to be attached , You need to “ Specific analysis of specific problems ”, Can't generalize , But the core principle is “ What's missing is what's missing ”.




Supplementary examples :

【 answer 】
It's easy to think of Rolle's theorem when we see that the title gives us three points

But it is found that these three points are not equal , Then we immediately think of Taylor's theorem

However, the intermediate value theorem of derivative cannot be directly used in the mathematics of postgraduate entrance examination ( Pay attention to the stem of this question [ No continuous ]), So what can we think of to avoid it ?
Construct auxiliary polynomials :


【 The real question 】


Set three Formula method ( Integral factor method )
【 Be careful 】
1、 Formula
No need to add any constant
, Because we only need to find an auxiliary function .
2、
It is not necessarily the conclusion to be proved , Sometimes it takes a little more deformation , But be sure to pay attention to —— Yes
When deforming , If both sides of the equation add something at the same time , Or divide something with it , It needs to be considered whether it is 0.




Need classified discussion :
①
If ξ≠0, It's in F'(ξ)=0 Make an appointment on both sides ξ, Get the conclusion to be proved ;
②
If ξ=0, That means 0 In the interval (a,b) Inside , That is, within the definition domain .
Again because F(x)=x²f(x), therefore F(0)=0, And because F(a)=F(b)=0, So to launch F There are three zeros , Namely a,0,b.
So we are 【a,0】 and 【0,b】 Use Rolle's theorem respectively , It can be proved that there are two non - 0 Of ξ1 and ξ2,
bring F'(ξ1)=F'(ξ2)=0, At this time due to ξ1 and ξ2 Not for 0, So you can be invited to .









【 notes 1】 The conclusion of this question is
, The most intuitive feeling is “ First derivative
Where is it ?”. therefore , This problem generally needs to be considered as the introduction of first-order derivatives
, To reach a reduced order The effect of .
【 notes 2】 Subtract from both sides of the equation
, In fact, it can , It's essentially the same thing .
【 notes 3】 If the conclusion already contains
, There is no need to introduce
了 , But sometimes we need to take the first derivative
To distribute reasonably , Make them reach a kind of “ Balance ”.
To distribute reasonably , Reach a balance

 【 notes 】 We will use this question as an example to show why in Mark's total Philosophy , Will emphasize “ Truth and error can be transformed into each other ”, It also hides the elements or sprouts of truth that will be revealed later .
【 notes 】 We will use this question as an example to show why in Mark's total Philosophy , Will emphasize “ Truth and error can be transformed into each other ”, It also hides the elements or sprouts of truth that will be revealed later .


In fact, the wrong solution is Lagrange from the inside out . The correct solution is from the outside to the inside Lagrange .
Set four Specific analysis of specific problems

Although we have already talked about the formula method , But formulas are not omnipotent , For this kind of problem, we need to observe the compact substructure , To analyze the result you want to prove is what the function looks like after deriving , Then try to restore it .
All in all , Restore the auxiliary function  The process of entropy reduction is moving in the direction of entropy reduction , So it is normal to have difficulties !
The process of entropy reduction is moving in the direction of entropy reduction , So it is normal to have difficulties !




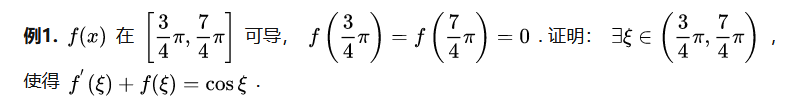




【 notes 】 This question should explain , Why doesn't the denominator be 0.








Pseudo double median problem !










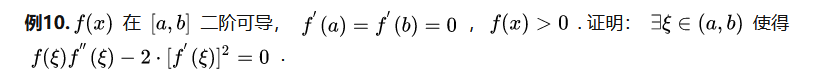







Routine five Separate constant and median , Direct pull or Cauchy





This topic is called the previous topic Example of routine 4 2


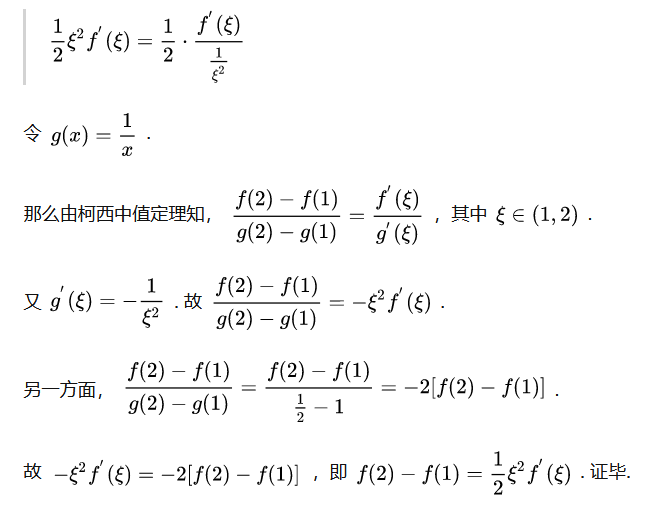




Routine six Double mean value theorem 【 False double median 】


【 notes 】 Take this topic as an example , Sum up a set of combination boxing , General killing ——
- ① Separate the complex median
- ② Restore it
- ③ An identical deformation or condition
- ④ Use the mean value theorem or Cauchy again
- ⑤ End of battle
【 Three median value example 】








Routine seven 【 The true double median theorem 】

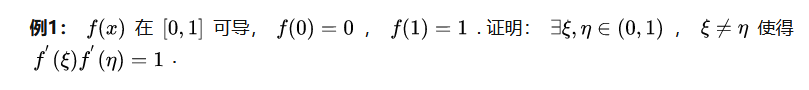



【n Median problem 】




【 example 4: The three median values can also be taken from two intervals 】


【 Add 】 These different median values do not necessarily come from different intervals , It may also come from the interior of the open interval , The other comes from the end of the interval , This kind of topic is very interesting , For example, the following questions .
【 Before class questions Pave the way ~ Otherwise, you may not be able to find the subject conditions 】
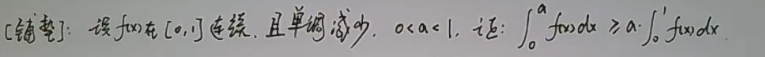


Routine 8 Find the median θ The limits of

tricks Four parts : Re expand , Compare the two forms 、 Establish the equation , Split median θ, Find the limit .



【 notes 】 Not clean , Two sides of an equation cannot be divided by the same .







【 example 4 The following question , Although it is also a calculation  The limits of , But because of
The limits of , But because of  The expression for is known , So we can easily solve the problem from the stem
The expression for is known , So we can easily solve the problem from the stem  The expression of , No difficulty 】
The expression of , No difficulty 】

【 Wrong solution 】



【 The correct solution 】

Routine nine Taylor Mean Value Theorem
If you want to prove that the conclusion contains higher-order derivation ( Second derivative above ): In general, you can use “ Taylor expansion with Lagrangian remainder ” To prove . In the specific operation , The most important thing is to be appropriate Select the expansion point  and Expanded point
and Expanded point  The location of .
The location of .
generally speaking , Select the point with more derivative information as the expansion point , Select the point that only tells the function value as the expanded point .
- tricks :
- Finite interval : Expand at the endpoint , Or expand at the midpoint
- Infinite interval : Expand at any point
Be careful :




【 notes 】
This problem needs to use Continuous function A corollary of the intermediate value theorem :
among
, or
because “ Derivative functions naturally satisfy the intermediate value theorem ”, So... In the condition “ The third derivative is continuous ” It can be changed to “ Third order differentiable ”!!
【 example 2 : Extreme points contain information about derivatives , So the function is often expanded at the extreme point 】



notes :

The next two questions , The stem condition does not tell the function value and derivative value at the experience point , Therefore, we can only guess how to select the expansion point and the expanded point according to the conclusion .




Experience : stay “ In the middle ” an

example 4: On a straight road , A car starts and stops , Shared unit time and completed unit journey .. prove : At least for a moment , The absolute value of its acceleration is not less than 4.


【 notes 】 For this kind of “ The function values of the two endpoints , Derivative values are known ” The topic , In order to make full use of the known conditions , Beginners may choose to expand each other at both ends , But the error will be very big ( Because Taylor expansion itself is an estimate , It requires that the distance between the expanded point and the expanded point should not be too large ), So using The midpoint expands at the endpoint .
Take advantage of the above considerations , You can easily kill the following question .



【 notes 】 Taylor + Expand at any point .


Start the infinite interval ~



Data from The postgraduate entrance examination competition ~
One's deceased father grind contest Kai GE's personal space _ Bili, Bili _Bilibili
Taylor Mean Value Theorem , Watch this video , enough !!!_ Bili, Bili _bilibili
Self use Arrangement ~
Title From ( Thank you ~
边栏推荐
- QT package the EXE file to solve the problem that "the program input point \u zdapvj cannot be located in the dynamic link library qt5cored.dll"
- 算力服务网络:一场多元融合的系统革命
- 记一次beego通过go get命令后找不到bee.exe的坑
- Once beego failed to find bee after passing the go get command Exe's pit
- 产业互联网的概念里有「互联网」字眼,但却是一个和互联网并不关联的存在
- 【STL源码剖析】STL六大组件功能与运用(目录)
- Application of TSDB in civil aircraft industry
- Once beego failed to find bee after passing the go get command Exe's pit
- 软件测试人员的7个等级,据说只有1%的人能做到级别7
- 进入阿里做测试员遥不可及?这里或许有你想要的答案
猜你喜欢
会自动化—10K,能做自动化—20K,你搞懂自动化测试没有?

I've been doing software testing for two years. I'd like to give some advice to girls who are still hesitating
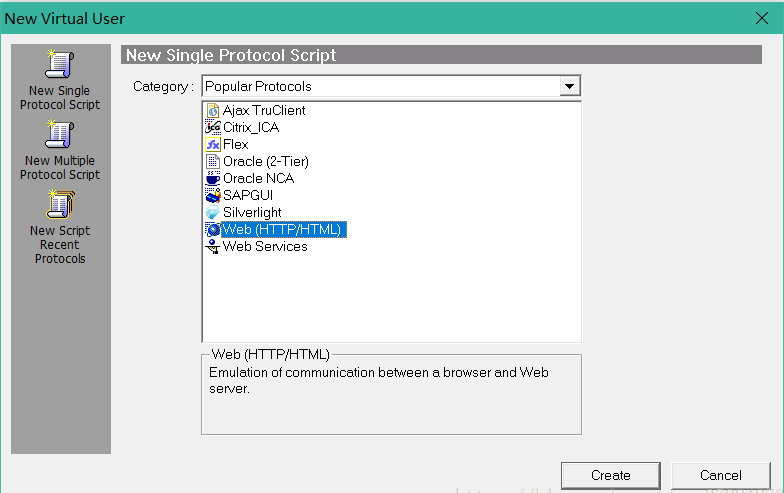
It's 2022, and you still don't know what performance testing is?

Redis

File system - basic knowledge of disk and detailed introduction to FAT32 file system

Yarn: unable to load file c:\users\xxx\appdata\roaming\npm\yarn PS1 because running scripts is prohibited on this system

一线城市软件测试工资——你拖后腿了吗

Random list random generation of non repeating numbers

入坑机器学习:一,绪论

华为、阿里等大厂程序员真的好找对象吗?
随机推荐
centos7.3修改mysql默认密码_详解Centos7 修改mysql指定用户的密码
Transformers Roberta如何添加tokens
Charles 抓包工具
记一次beego通过go get命令后找不到bee.exe的坑
[I.MX6UL] U-Boot移植(六) 网络驱动修改 LAN8720A
把 Oracle 数据库从 Windows 系统迁移到 Linux Oracle Rac 集群环境(1)——迁移数据到节点1
请问polarDB数据库可以通过mysql进行数据源连接吗
商城项目 pc----商品详情页
When an interface has an exception, how do you analyze the exception?
The Oracle 11g RAC cluster database cannot be started due to directory permission errors
【FPGA】串口以命令控制温度采集
转行软件测试2年了,给还在犹豫的女生一点建议
qt打包exe文件,解决“无法定位程序输入点_ZdaPvj于动态链接库Qt5Cored.dll”
背了八股文,六月赢麻了……
How transformers Roberta adds tokens
Summary of stack frame in arm assembly
Rod and Schwartz cooperated with ZhongGuanCun pan Lianyuan Institute to carry out 6G technology research and early verification
Advanced usage of groovy
Kaggle 专利匹配比赛赛后总结
把 Oracle 数据库从 Windows 系统迁移到 Linux Oracle Rac 集群环境(2)——将数据库转换为集群模式

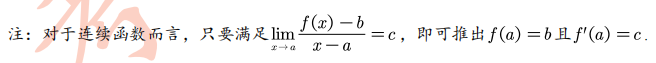

 Purpose , It mainly refers to those in the question stem “ uneven ” The function value and derivative value of are all “ Zeroing ”, Thus making
Purpose , It mainly refers to those in the question stem “ uneven ” The function value and derivative value of are all “ Zeroing ”, Thus making 

 yes n Sub polynomial , And we end up with auxiliary functions
yes n Sub polynomial , And we end up with auxiliary functions  Continuously find n Secondary derivative , So we get
Continuously find n Secondary derivative , So we get  ,
, ,
, , You need to construct a
, You need to construct a  Polynomial fitting . because n Polynomial of degree has
Polynomial fitting . because n Polynomial of degree has  A coefficient of , So the question is in the stem
A coefficient of , So the question is in the stem 
 No need to add any constant
No need to add any constant  , Because we only need to find an auxiliary function .
, Because we only need to find an auxiliary function . It is not necessarily the conclusion to be proved , Sometimes it takes a little more deformation , But be sure to pay attention to —— Yes
It is not necessarily the conclusion to be proved , Sometimes it takes a little more deformation , But be sure to pay attention to —— Yes  , The most intuitive feeling is “ First derivative
, The most intuitive feeling is “ First derivative  Where is it ?”. therefore , This problem generally needs to be considered as the introduction of first-order derivatives
Where is it ?”. therefore , This problem generally needs to be considered as the introduction of first-order derivatives  , In fact, it can , It's essentially the same thing .
, In fact, it can , It's essentially the same thing . , There is no need to introduce
, There is no need to introduce 

![\xi\in [x_{1},x{_2}]](http://img.inotgo.com/imagesLocal/202206/25/202206242258097597_71.gif) , or
, or ![\xi\in [x_{2},x{_1}]](http://img.inotgo.com/imagesLocal/202206/25/202206242258097597_10.gif)