当前位置:网站首页>2016CCPC网络选拔赛C-换根dp好题
2016CCPC网络选拔赛C-换根dp好题
2022-07-25 15:23:00 【塔子哥来了】
题目大意:
给一颗树,带点权和边权.问你每个点,得到的最大价值.(点权代表价值边权代表花费).每个点只能拿一次,边反复计算花费.
题目思路:
容易想出一种树形dp后换根的思路:
d p ( i , 0 / 1 ) dp(i,0/1) dp(i,0/1)代表以 i i i为根的子树,最后回到/不回到i点的最大价值.
d p ( i , 1 ) = ∑ j ∈ S o n i m a x ( d p ( j , 1 ) − 2 ∗ w i , 0 ) dp(i,1)=\sum_{j\in Son_i}max(dp(j,1)-2*w_i,0) dp(i,1)=∑j∈Sonimax(dp(j,1)−2∗wi,0)
d p ( i , 0 ) = d p ( i , 1 ) − m a x j ∈ S o n i ( m a x ( d p ( j , 0 ) − w i , 0 ) − m a x ( d p ( j , 1 ) − 2 ∗ w i , 0 ) ) dp(i,0)=dp(i,1)-max_{j\in Son_i}(max(dp(j,0)-w_i,0)-max(dp(j,1)-2*w_i,0)) dp(i,0)=dp(i,1)−maxj∈Soni(max(dp(j,0)−wi,0)−max(dp(j,1)−2∗wi,0))
下面令 g x 1 = m a x ( d p ( j , 1 ) − 2 ∗ w i , 0 ) , g x 2 = m a x ( d p ( j , 0 ) − w i , 0 ) gx_1=max(dp(j,1)-2*w_i,0),gx_2=max(dp(j,0)-w_i,0) gx1=max(dp(j,1)−2∗wi,0),gx2=max(dp(j,0)−wi,0)
再维护 s e ( i , 0 ) = d p ( i , 1 ) − 2 j ∈ S o n i t h ( m a x ( d p ( j , 0 ) − w i , 0 ) − m a x ( d p ( j , 1 ) − 2 ∗ w i , 0 ) ) se(i,0)=dp(i,1)-2^{th}_{j\in Son_i}(max(dp(j,0)-w_i,0)-max(dp(j,1)-2*w_i,0)) se(i,0)=dp(i,1)−2j∈Sonith(max(dp(j,0)−wi,0)−max(dp(j,1)−2∗wi,0))
和 t o ( i ) to(i) to(i)
(后面再讲这俩干嘛的)
转移完,考虑第二遍dfs,将父亲当作子树,把它的影响考虑进来
令新一轮的dp为 n d p , s s e , t t o ndp,sse,tto ndp,sse,tto
注意转移的时候要将父亲dp中对于该点的贡献取消,这个部分是最复杂的:
1.当更新 n d p ( i , 1 ) ndp(i,1) ndp(i,1)时,
父亲 f a fa fa对点 i i i的贡献 g x 3 = m a x ( n d p ( f a , 1 ) − g x 1 − w i , 0 ) gx_3=max(ndp(fa,1)-gx_1-w_i,0) gx3=max(ndp(fa,1)−gx1−wi,0)
那么 n d p ( i , 1 ) = d p ( i , 1 ) + g x 3 ndp(i,1)=dp(i,1)+gx_3 ndp(i,1)=dp(i,1)+gx3
n d p ( i , 0 ) = d p ( i , 0 ) + g x 3 ndp(i,0)=dp(i,0)+gx_3 ndp(i,0)=dp(i,0)+gx3 (先假设最后不留在父节点)
s s e ( i ) = s e ( i ) + g x 3 sse(i)=se(i)+gx_3 sse(i)=se(i)+gx3
2.当更新 n d p ( i , 0 ) ndp(i,0) ndp(i,0)时(most hard)
这个时候父亲节点对 i i i的贡献就很复杂了,分两种情况:
2.1当 d p ( f a , 0 ) dp(fa,0) dp(fa,0)最后不是落在子树 i i i时,父亲 f a fa fa对点 i i i的贡献 g x 4 = m a x ( n d p ( f a , 1 ) − g x 1 − w i , 0 ) gx_4=max(ndp(fa,1)-gx_1-w_i,0) gx4=max(ndp(fa,1)−gx1−wi,0)
2.2 否则,我们需要重新规划 d p ( f a , 0 ) dp(fa,0) dp(fa,0),让他最后的终点不要落在 i i i中。那么就落在哪?
次优解!
所以此时我们需要多维护 次优值 s e ( i ) se(i) se(i)和 最优值落在的儿子节点 t o ( i ) to(i) to(i) 用于判断是否落在子树.
那么贡献 g x 5 = m a x ( s s e ( f a , 1 ) − g x 1 − w i , 0 ) gx_5=max(sse(fa,1)-gx_1-w_i,0) gx5=max(sse(fa,1)−gx1−wi,0)
这时令 t m p = d p ( i , 1 ) + g x 4 / g x 5 − w tmp=dp(i,1)+gx_4/gx_5-w tmp=dp(i,1)+gx4/gx5−w
用 t m p tmp tmp来更新当前节点的最后留向
1.若 t m p ≥ n d p ( i , 0 ) tmp \geq ndp(i,0) tmp≥ndp(i,0) 代表往父亲节点走并留在那比(假设不往父亲节点走)更优,我们需要重新规划该点的 s s e , t t o sse,tto sse,tto
s s e ( i ) = n d p ( i , 0 ) , t t o = f a sse(i)=ndp(i,0),tto=fa sse(i)=ndp(i,0),tto=fa
2.否则无法更新.
PS:很久没写这么复杂的题目了。。不过还是独立完成了
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pii pair<int,int>
#define pb push_back
#define mp make_pair
#define vi vector<int>
#define vll vector<ll>
#define fi first
#define se second
const int maxn = 1e5 + 5;
const int mod = 1e9 + 7;
int dp[maxn][2] , se[maxn] , f[maxn][2] , to[maxn] , a[maxn];
int tto[maxn] , sse[maxn];
vector<pii> e[maxn];
void dfs (int u , int fa){
dp[u][0] = dp[u][1] = 0;
for (auto &g : e[u]){
int v = g.first , w = g.second;
if (v == fa) continue;
dfs(v , u);
dp[u][1] += max(dp[v][1] - 2 * w , 0);
}
vector<pii> res;
for (auto &g : e[u]){
int v = g.first , w = g.second;
if (v == fa) continue;
int tmp = max(max(dp[v][0] - w , 0) - max(dp[v][1] - 2 * w , 0) , 0);
res.push_back({
tmp , v});
}
sort(res.begin() , res.end());
reverse(res.begin() , res.end());
if (res.size() > 0){
dp[u][0] = dp[u][1] + res[0].first;
to[u] = res[0].second;
if (res.size() == 1) se[u] = 0;
else se[u] = dp[u][1] + res[1].first;
}else {
se[u] = 0;
}
dp[u][0] += a[u];
dp[u][1] += a[u];
se[u] += a[u];
return ;
}
void dfs1 (int u , int fa , int ww){
f[u][0] = dp[u][0];
f[u][1] = dp[u][1];
tto[u] = to[u];
sse[u] = se[u] + max(w , 0);
int gx = max(0 , dp[u][1] - 2 * ww);
int w = f[fa][1] - gx - 2 * ww; // 选择fa并回来所带来的价值w
f[u][1] = dp[u][1] + max(w , 0);
f[u][0] = dp[u][0] + max(w , 0);
// 选择fa并不回来的价值ggg
int ggg;
if (tto[fa] == u) ggg = sse[fa] - gx - ww;
else ggg = f[fa][0] - gx - ww;
int ttt = dp[u][1] + max(ggg , 0);
// f[u][0] ttt
if (ttt >= f[u][0]){
sse[u] = f[u][0];
f[u][0] = ttt;
tto[u] = fa;
}else if (ttt >= sse[u]){
sse[u] = ttt;
}
for (auto &g : e[u]){
int v = g.first , w = g.second;
if (v == fa) continue;
dfs1(v , u , w);
}
return ;
}
int main()
{
ios::sync_with_stdio(false);
int t; cin >> t;
int cnt = 0;
while (t--){
int n; cin >> n;
for (int i = 1 ; i <= n ; i++){
e[i].clear();
tto[i] = sse[i] = dp[i][0] = dp[i][1] = se[i] = f[i][0] = f[i][1] = to[i] = 0;
}
for (int i = 1 ; i <= n ; i++) cin >> a[i];
for (int i = 1 ; i < n ; i++){
int x , y , z; cin >> x >> y >> z;
e[x].pb({
y , z});
e[y].pb({
x , z});
}
dfs (1 , 0);
dfs1(1 , 0 , 0);
cout << "Case #" << (++cnt) << ":" << endl;
for (int i = 1 ; i <= n ; i++){
cout << max(f[i][0] , f[i][1]) << endl;
}
}
return 0;
}
边栏推荐
- HBCK fix problem
- 理解“平均负载”
- Implementation of asynchronous FIFO
- 带你详细认识JS基础语法(建议收藏)
- 在网页上实现任意格式的音视频快速播放功能的开发总结。
- Object.prototype. Hasownproperty() and in
- 看到很多App出现闪烁的图片,特别是会员页面
- 记一次Spark报错:Failed to allocate a page (67108864 bytes), try again.
- See a lot of blinking pictures on apps, especially the member page
- matlab randint,Matlab的randint函数用法「建议收藏」
猜你喜欢

Use the command to check the WiFi connection password under win10 system
Idea remotely submits spark tasks to the yarn cluster

带你创建你的第一个C#程序(建议收藏)

图论及概念
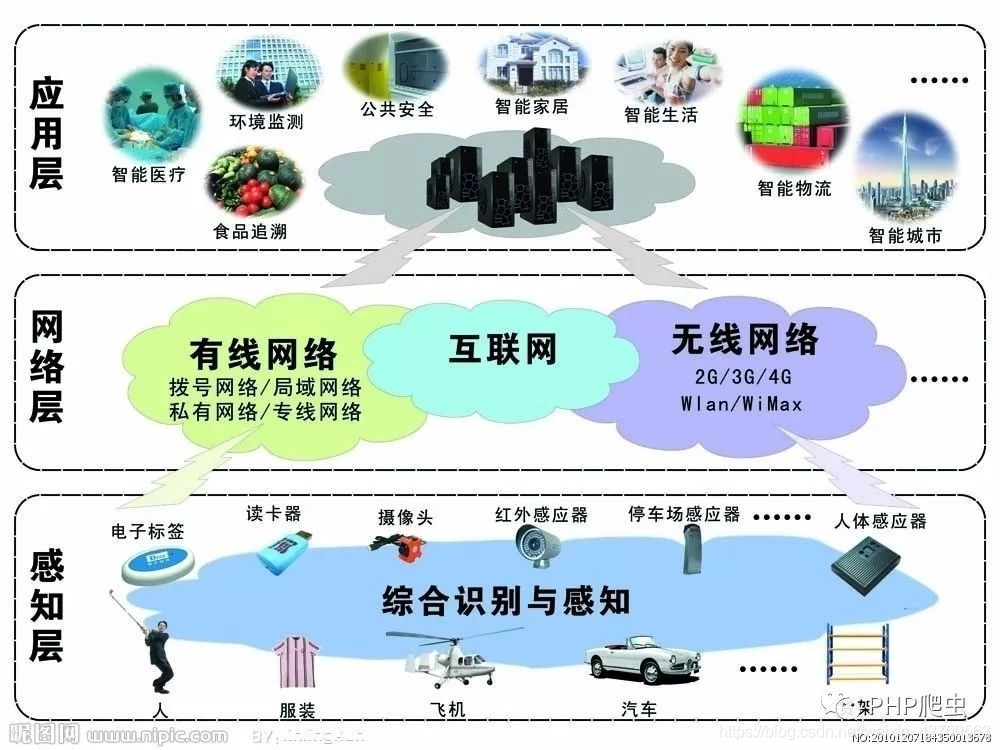
What is the Internet of things

How to solve the problem of scanf compilation error in Visual Studio
Simulate setinterval timer with setTimeout
matlab 优化工具 manopt 安装

ML - 自然语言处理 - 自然语言处理简介

《图书馆管理系统——“借书还书”模块》项目研发阶段性总结
随机推荐
Image cropper example
Spark memory management mechanism new version
Reflection - Notes
Node learning
Endnote 无法编辑range 解决
Submarine cable detector tss350 (I)
Spark sql 常用时间函数
Application of C language array in Sanzi chess -- prototype of Queen n problem
JVM garbage collector details
Run redis on docker to start in the form of configuration file, and the connection client reports an error: server closed the connection
The number of query results of maxcompute SQL is limited to 1W
MATLAB 如何生产随机复序列
Xcode添加mobileprovision证书文件报错:Xcode encountered an error
2021HNCPC-E-差分,思维
Spark提交参数--files的使用
redis淘汰策列
Spark submission parameters -- use of files
Spark SQL UDF function
Instance tunnel use
How much memory can a program use at most?