当前位置:网站首页>汉诺塔问题
汉诺塔问题
2022-06-22 05:03:00 【姜学迁】
汉诺塔:简单来说,就是一个大盘子和一堆小盘子的移动游戏。
先把小盘子们移到中间,再把大盘子移到最后,最后把小盘子们摞到大盘子上面。
如果是两个盘子,小盘子移到中间,大盘子移到最后,小盘子再放到大盘子上面来,很符合这个流程。

如果是三个盘子呢,此时我们应该分开来看。
先不看大盘子,对小盘子们来说,它们的目标是全部放到中间。这么来看,两个小盘子又是一个汉诺塔问题,只不过我们最开始说的“中间”对新的汉诺塔问题而言,变成了“最后”。
好像有些抽象,我们编号看看。
我们标记整个问题:A为起始,B为中间,C为目标。
对于两个小盘子来说:A为起始,B为目标,C为中间。
我们先忽略大盘子,当它不存在,处理小盘子。移动两个汉诺塔,还是很简单的。
进行汉诺塔排序:A——>C,A——>B,C——>B。完成了整个过程。两个盘子的游戏结束。
再让大盘子回来,并且执行A——>C。
此时两个小盘子又是一个经典的汉诺塔问题,而且B成了起始柱,A成了中间柱,C成了目标柱。
再进行一次汉诺塔排序:B——>A,B——>C,A——>C。
汉诺塔排列完成。
那么根据这个过程,我们来写代码:
void hanoi(int n, char A, char B, char C) //三个柱子,总问题,A为起始,B为中间,C为目标。
{
if (n==1) //一个盘子的情况,起始——>目标
{
printf("%c——>%c\n", A, C);
}
else //两个盘子的情况,A为起始,B为目标,C为中间。
{
hanoi(n - 1, A, C, B); //起始——>目标,因为2-1=1,所以直接排
printf("%c——>%c\n", A, C); //大盘子A——>C
hanoi(n - 1, B, A, C); //小盘子从B目标转到C目标,因为2-1=1,所以直接排
}
}
所有的大于两个盘子的情况,都会落实到一次次的递归当中。我们关心的是一个盘子、两个盘子怎么移动,最多关心三个盘子怎么移动。每一次递归,柱子的定位都会发生改变,而盘子的变化是有限的。我们的思维认为,固定的柱子不变,活动的盘子移动,但在递归的过程中,柱子是在变化的。
#include <stdio.h>
void hanoi(int n, char A, char B, char C)
{
if (n==1)
{
printf("%c——>%c\n", A, C);
}
else
{
hanoi(n - 1, A, C, B);
printf("%c——>%c\n", A, C);
hanoi(n - 1, B, A, C);
}
}
int main()
{
hanoi(3, 'A', 'B', 'C');
return 0;
}
说真的,似懂非懂的感觉最难受了。我能感觉到它就是这个样,但就是想不通整个过程。/狗头
边栏推荐
- 使用Chrome调试微信内置浏览器
- Accelerate the promotion of industrial Internet, and map out a new blueprint for development
- Database - basic knowledge
- [user guide] create an environment using public CONDA
- Common knowledge arrangement of numpy database
- Browser -- a collection of common search operators -- use / instance
- NHibernate method for viewing generated SQL statements
- How much is London gold
- mysql day02课堂笔记
- 数据的备份与恢复
猜你喜欢
![[camp] at the beginning, improve [leopard] power - vivo activity plug-in management platform](/img/75/6a129de59c21b783622ba31f77f647.jpg)
[camp] at the beginning, improve [leopard] power - vivo activity plug-in management platform

Will swift compile to native code- Does Swift compile to native code?

Leetcode -- the kth largest node of the binary search tree (traversal by means of middle order)
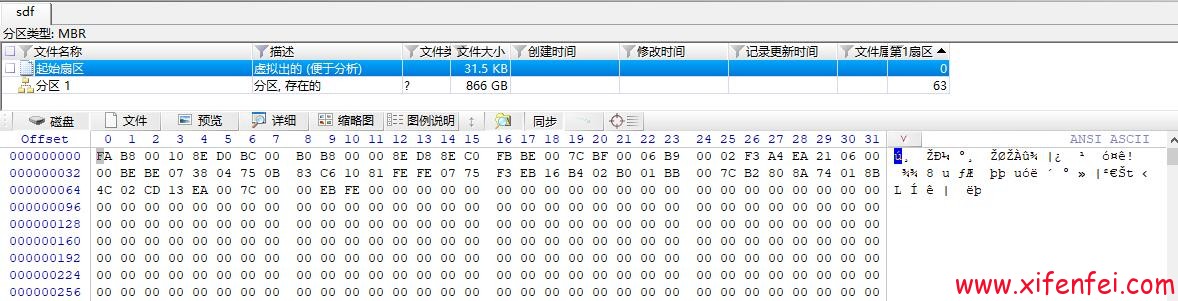
Ora-15063: ASM discovered an insufficient number of disks for diskgroup

数据库---基础知识

Target detection algorithm based on deep learning interview essential (rcnn~yolov5)
![[scientific research notes] focal loss](/img/ca/4a30fd925b87ed2baa2523d8dbf59d.png)
[scientific research notes] focal loss

Final examination questions of Database Principles

Database - basic knowledge

ORA-15063: ASM discovered an insufficient number of disks for diskgroup 恢複---惜分飛
随机推荐
The yarn deployment mode depends on the pre upload settings
JUC - 线程中断与线程等待、唤醒(LockSupport)
6. Local - custom filter factory
Reconstructing thinking series 2-functions and variables
并发编程——线程池
10道不得不会的 Redis 面试题
What is cloud hosting and what are its advantages?
获取DPI函数返回值永远是96 | 获取DPI函数返回值不正确 | GetDpiForMonitor/GetDeviceCaps返回值不正确的原因
UC San Diego | evit: using token recombination to accelerate visual transformer (iclr2022)
Great! Huaibei and Huaibei enterprises are approved to use special marks for geographical indication products
Pull down refresh, push up load (easy to use, finally)
【使用指南】清华源的使用
使用Chrome调试微信内置浏览器
Lua notes
zipimport.ZipImportError:
Go learning (II. Built in container)
Software architecture and pattern: structure, component and relationship
Go learning (I. Basic Grammar)
Accelerate the promotion of industrial Internet, and map out a new blueprint for development
Ora - 15063: ASM discovered an insufficient number of Disks for diskgroup Recovery - - -