当前位置：网站首页>NF RESNET: network signal analysis worth reading after removing BN normalization | ICLR 2021

NF RESNET: network signal analysis worth reading after removing BN normalization | ICLR 2021

2022-06-22 15:15:00 【Xiaofei's algorithm Engineering Notes】

The paper proposes NF-ResNet, According to the actual signal transmission of the network , simulation BatchNorm Performance in the transfer of mean and variance , Instead of BatchNorm. The experiment and analysis of this paper are very sufficient , The effect is also very good . The theoretical results of some initialization methods are correct , But there will be deviation in actual use , The paper finds this point through practical analysis to supplement , We have implemented the principle that practice produces true knowledge
source ： Xiaofei's algorithm Engineering Notes official account

The paper : Characterizing signal propagation to close the performance gap in unnormalized ResNets

Address of thesis ：https://arxiv.org/abs/2101.08692

Introduction

BatchNorm It is the core computing component in deep learning , Most of SOTA Image models all use it , The main advantages are as follows ：

Smooth loss curve , You can use a greater learning rate to learn .
according to minibatch The calculated statistics are equivalent to the current batch Introduce noise , There is regularization , Prevent over fitting .
In the initial stage , Constrains the weight of the residual branch , Ensure that the deep residual network has good information transmission , Can train ultra deep network .

However , Even though BatchNorm very good , But it still has the following shortcomings ：

Performance acceptance batch size Great influence ,batch size Poor performance for hours .
Bring about the problem of inconsistent usage in training and reasoning .
Increase memory consumption .
Common error sources when implementing models , Especially distributed training .
Because of the accuracy , Difficult to replicate training results on different hardware .

at present , Many studies have begun to look for alternatives BatchNorm Normalization layer of , But these alternative layers either don't work , Or it will bring new problems , For example, increase the computational cost of reasoning . Other studies try to remove the normalization layer , For example, initialize the weight of the residual branch , Make its output zero , Ensure that most of the information at the beginning of the training passes skip path To pass . Although it can train a deep network , But the accuracy of the network using simple initialization method is poor , And such initialization is difficult to use in more complex networks .
therefore , The paper hopes to find an effective training method that does not contain BatchNorm The method of depth residual network , And the performance of the test set is comparable to the current SOTA, The main contributions of this paper are as follows ：

Propose a signal propagation diagram (Signal Propagation Plots, SPPs), It can assist in observing the propagation of reasoning signals in the initial stage , Determine how to design without BatchNorm Of ResNet To achieve a similar signal transmission effect .
Verification found no BatchNorm Of ResNet The key to the bad effect lies in the nonlinear activation (ReLU) Use , The mean value of the output after nonlinear activation is always positive , As a result, the average value of the weight increases sharply with the increase of the network depth . So he put forward Scaled Weight Standardization, It can prevent the growth of signal mean value , Significantly improved performance .
Yes ResNet Conduct normalization-free Modification and addition Scaled Weight Standardization Training , stay ImageNet And the original ResNet It has considerable performance , The number of layers reaches 288 layer .
Yes RegNet Conduct normalization-free reform , combination EfficientNet Blend scaling of , constructed NF-RegNet series , It has reached the same level as... In different calculations EfficientNet Quite good performance .

Signal Propagation Plots

Many studies theoretically analyze ResNet Signal propagation , However, it is rare to verify the feature scaling of different layers in the design or magic change network . actually , Forward reasoning with arbitrary input , Then the statistical information of different location characteristics of the network is recorded , It can intuitively understand the information transmission status and find hidden problems as soon as possible , Don't have to go through a long training failure . therefore , This paper presents a signal propagation diagram (Signal Propagation Plots,SPPs), Input random Gauss input or real training sample , Then each residual is counted separately block The following information is output ：

Average Channel Squared Mean, stay NHW Dimension calculates the square of the mean ( Balance the positive and negative mean ), And then in C The dimension calculates the average , The closer to zero, the better .
Average Channel Variance, stay NHW Dimension calculates variance , And then in C The dimension calculates the average , Used to measure the amplitude of a signal , You can see whether the signal is exploding or decaying .
Residual Average Channel Variance, Only the residual branch output is calculated , Used to evaluate whether the branch is properly initialized .

Papers on common BN-ReLU-Conv Structure and unusual ReLU-BN-Conv The structure is statistically tested , The experimental network is 600 layer ResNet, use He initialization , Definition residual block by \(x_{l+1}=f_{l}(x_{l}) + x_{l}\), from SPPs The following phenomena can be found ：

Average Channel Variance As the network depth increases linearly , And then in transition block Reset to a lower value at . This is because at the beginning of training ,residual block The variance of the output of is \(Var(x_{l+1})=Var(f_{l}(x_{l})) + Var(x_{l})\), Keep accumulating residual branch and skip path The variance of . And in the transition block It's about ,skip path The input of is BatchNorm Handled , therefore block The variance of the output is reset directly .

BN-ReLU-Conv Of Average Squared Channel Means With the increasing depth of the network , although BatchNorm The output of is zero mean , But after ReLU Then it becomes a positive mean , And again skip path Add up and add up until transition block Appearance , This phenomenon can be called mean-shift.

BN-ReLU Of Residual Average Channel Variance about 0.68,ReLU-BN Of is about 1.BN-ReLU The variance of is decreased mainly due to ReLU, We will analyze later , But the theory should be 0.34 about , And everyone here transition block The residual branch output of is 1, It's a little strange. , If you know the reader, please comment or send a private letter .

If you remove it directly BatchNorm,Average Squared Channel Means and Average Channel Variance Will continue to increase , This is also the reason why the deep network is difficult to train . So we need to get rid of it BatchNorm, We must try to simulate BatchNorm Signal transmission effect .

Normalizer-Free ResNets(NF-ResNets)

According to the preceding SPPs, The paper designs a new redsidual block\(x_{l+1}=x_l+\alpha f_l(x_l/\beta_l)\), The main simulation is BatchNorm Performance on mean and variance , As follows ：

\(f(\cdot)\) by residual branch The calculation function of , This function requires special initialization , Ensure that the initial stage has the function of maintaining variance , namely \(Var(f_l(z))=Var(z)\), Such constraints can help better explain and analyze the signal growth of the network .
\(\beta_l=\sqrt{Var(x_l)}\) Is a fixed scalar , The value is the standard deviation of the input characteristic , Guarantee \(f_l(\cdot)\) Is the unit variance .
\(\alpha\) Is a super parameter , Used to control the block The growth rate of variance between .

According to the design above , Given \(Var(x_0)=1\) and \(\beta_l=\sqrt{Var(x_l)}\), According to the \(Var(x_l)=Var(x_{l-1})+\alpha^2\) Directly calculate the \(l\) individual residual block The variance of the output of . To simulate ResNet The cumulative variance in transition block Is reset , Need to put transition block Of skip path The input of is reduced to \(x_l/\beta_l\), Make sure that each stage At the beginning transition block The output variance satisfies \(Var(x_{l+1})=1+\alpha^2\). Apply the above simple scaling strategy to the residual network and remove BatchNorm layer , Got it. Normalizer-Free ResNets(NF-ResNets).

ReLU Activations Induce Mean Shifts

Papers on the use of He The initialization of the NF-ResNet Conduct SPPs analysis , The result is shown in Fig. 2, Two unexpected phenomena have been found ：

Average Channel Squared Mean As the network deepens, it continues to increase , The value is large enough to exceed the variance , Yes mean-shift The phenomenon .
Follow BN-ReLU-Conv similar , The variance of the residual branch output is always less than 1.

To verify the above phenomena , The paper will be the ReLU Remove and then SPPs analysis . Pictured 7 Shown , When removing ReLU after ,Average Channel Squared Mean Close to the 0, And the output of the residual branch is close to 1, This indicates that ReLU Led to mean-shift The phenomenon .
The paper also analyzes this phenomenon from a theoretical point of view , First define the transformation \(z=Wg(x)\),\(W\) Is an arbitrary and fixed matrix ,\(g(\cdot)\) To act on independent identically distributed inputs \(x\) Upper elememt-wise Activation function , therefore \(g(x)\) It is also independent and identically distributed . Suppose each dimension \(i\) There are \(\mathbb{E}(g(x_i))=\mu_g\) as well as \(Var(g(x_i))=\sigma^2_g\), The output \(z_i=\sum^N_jW_{i,j}g(x_j)\) The mean and variance of are ：

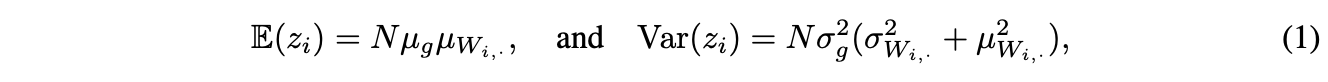
among ,\(\mu w_{i,.}\) and \(\sigma w_{i,.}\) by \(W\) Of \(i\) That's ok (fan-in) The mean and variance of ：

When \(g(\cdot)\) by ReLU When the function is activated , be \(g(x)\ge 0\), It means that the inputs of subsequent linear layers are positive mean values . If \(x_i\sim\mathcal{N}(0,1)\), be \(\mu_g=1/\sqrt{2\pi}\). because \(\mu_g>0\), If \(\mu w_i\) It is also non-zero , be \(z_i\) There is also a non-zero mean . It should be noted that , Even if \(W\) From a distribution with a mean of zero , The actual matrix mean will not be zero , Therefore, the output of any dimension of the residual branch will not be zero , As the depth of the network increases , It's getting harder to train .

Scaled Weight Standardization

In order to eliminate mean-shift Phenomena and guaranteed residual branching \(f_l(\cdot)\) Having the property of invariable variance , The paper draws lessons from Weight Standardization and Centered Weight Standardization, Put forward Scaled Weight Standardization(Scaled WS) Method , This method reinitializes the weight of the convolution layer as follows ：

\(\mu\) and \(\sigma\) Is a convolution kernel fan-in The mean and variance of , A weight \(W\) The initial value is Gaussian weight ,\(\gamma\) Is a fixed constant . Generation into the formula 1 We can draw , about \(z=\hat{W}g(x)\), Yes \(\mathbb{E}(z_i)=0\), In addition to the mean-shift The phenomenon . in addition , Variance becomes \(Var(z_i)=\gamma^2\sigma^2_g\),\(\gamma\) The value is determined by the activation function used , The variance can be kept constant .
Scaled WS The added cost of training is very small , And with the batch Data independent , There is no extra cost in reasoning . in addition , The calculation logic during training and testing is consistent , It is also friendly to distributed training . From the picture 2 Of SPPs The curve shows , Join in Scaled WS Of NF-ResNet-600 The performance of the heel ReLU-BN-Conv Very similar .

Determining Nonlinerity-Specific Constants

The last factor is \(\gamma\) Determination of value , Ensure that the variance of the residual branch output is close to at the initial stage 1.\(\gamma\) The value is determined by the nonlinear activation type used by the network , Assume a nonlinear input \(x\sim\mathcal{N}(0,1)\), be ReLU Output \(g(x)=max(x,0)\) It is equivalent to that the variance is \(\sigma^2_g=(1/2)(1-(1/\pi))\) From the Gaussian distribution sampling . because \(Var(\hat{W}g(x))=\gamma^2\sigma^2_g\), Can be set up \(\gamma=1/\sigma_g=\frac{\sqrt{2}}{\sqrt{1-\frac{1}{\pi}}}\) To guarantee \(Var(\hat{W}g(x))=1\). Although the real input does not exactly match \(x\sim \mathcal{N}(0,1)\), In practice, the above \(\gamma\) Setting still has a good performance .
For other complex nonlinear activation , Such as SiLU and Swish, Formula derivation involves complex integrals , It can't even be rolled out . under these circumstances , Numerical approximation can be used . First, multiple samples are sampled from the Gaussian distribution \(N\) Dimension vector \(x\), Calculate the actual variance of the active output of each vector \(Var(g(x))\), Then take the square root of the mean of the actual variance .

Other Building Block and Relaxed Constraints

The core of this article is to maintain correct information transmission , So many common network structures have to be modified . Just like choosing \(\gamma\) Have the same value , Necessary modifications can be judged through analysis or practice . such as SE modular \(y=sigmoid(MLP(pool(h)))*h\), Output needs to be consistent with \([0,1]\) Multiply by the weight of , Cause information transmission to weaken , The network becomes unstable . Use the numerical approximation mentioned above for separate analysis , It is found that the expected variance is 0.5, This means that the output needs to be multiplied by 2 To restore correct information transmission .
actually , Sometimes relatively simple network structure modification can maintain good information transmission , And sometimes even if the network structure is not modified , The network itself can also be very robust to the information attenuation caused by the network structure . therefore , The paper also tries to maintain the stability of training under the premise of , test Scaled WS The maximum relaxation of the constraints of the layer . such as , by Scaled WS Layer restores some convolution expressiveness , Add learnable scaling factors and offsets , Used for weight multiplication and nonlinear output addition respectively . When these learnable parameters have no constraints , The stability of training has not been greatly affected , On the contrary, it is more than 150 Layer network training is helpful . therefore ,NF-ResNet The constraint is relaxed directly , Add two learnable parameters .
The appendix of the paper has detailed network implementation details , Those who are interested can go and have a look .

Summary

To sum up ,Normalizer-Free ResNet The core of is as follows ：

Calculate the expected variance of forward propagation \(\beta^2_l\), After each residual error block Steady increase \(\alpha^2\), The input of the residual branch needs to be reduced \(\beta_l\) times .
take transition block in skip path The convolution input of is reduced \(\beta_l\) times , And in transition block Then reset the variance to \(\beta_{l+1}=1+\alpha^2\).
Use... For all convolution layers Scaled Weight Standardization initialization , be based on \(x\sim\mathcal{N}(0,1)\) Calculate the activation function \(g(x)\) Corresponding \(\gamma\) value , Is the reciprocal of the expected standard deviation of the output of the active function \(\frac{1}{\sqrt{Var(g(x))}}\).

Experiments

contrast RegNet Of Normalizer-Free Comparison of variants with other methods , be relative to EfficientNet Or almost , But it's very close .

Conclusion

The paper proposes NF-ResNet, According to the actual signal transmission of the network , simulation BatchNorm Performance in the transfer of mean and variance , Instead of BatchNorm. The experiment and analysis of this paper are very sufficient , The effect is also very good . The theoretical results of some initialization methods are correct , But there will be deviation in actual use , The paper finds this point through practical analysis to supplement , We have implemented the principle that practice produces true knowledge .