当前位置：网站首页>初识二叉搜索树
初识二叉搜索树
2022-07-30 16:11:00 【51CTO】
写在前面
我们今天来谈一个比较简单的话题，算是二叉树的进阶，但是里面的内容我们都是说过了，主要是为了后面的比较难得二叉树做准备，先来看看今天的内容吧.
搜索二叉树
这个是我们学习下面AVL树,红黑树的基础,今天的就比较简单了.
什么是 搜索二叉树
这个也可以叫二叉搜索树,反正名字是不重要的,关键是它的条件要求.二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:
- 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
可以这么说,一般二叉搜索树的中树节点里面的值是不相等的,当然我们也可以存放相等的,那么就变成的另外的一棵树了,这是在后面谈的.
搜索树的时间复杂度
大家看一次名字你就会发现,二叉搜索树,肯定主要的内容是搜索啊,这里我们看一下他们是如何搜索的.
我们拿到一个值,去和根节点去比,入过比他大,就去右子树中找,比他小,就去左子树中找,相等就找到了,这就是二叉搜索的流程.
那么我想问问,它的时间复杂度是多少?大家一看,这不就是查找树的高度次吗,应该是O(lgN)吧?记住,这是搜索二叉树最大为误区,它的时间复杂度是 O(N),主要是这个树太过正常,如果是一颗不正常的树,你就会发现了.
二叉搜索的遍历
要是仔细的朋友,你就会发现,,二叉搜索树的中序遍历就是一个升序的数组,这一点也是二叉搜索树的特点.
实现二叉搜索树
我们先来实现一个简单的二叉搜索树,先来看看它的底层是什么样的,后面来更好的了解它的应用.
准备节点
这个倒是挺简单的,一般而言,想这些节点的都是用struct来声明和定义类的,这里我们还用了模板,不过也没有什么可以说的.
二叉搜索树
现在我们就可以开始它的是实现了,我们发现,只需要准备一个成员变量来存放根节点就可以了.
中序遍历
我们先来一个中序遍历,主要是为了后面的插入删除等好验证.
大家先说一下,下面的代码可以吗?
看着挺行的,里面的考虑的也比较周全,可惜存在一个问题,我们在类外如何调用这个函数要知道,我们是无法拿到根节点的啊,除非你再写一个得到根节点的函数.
这里我们需要在把这个函数封装一层,这样为了更好的使用,下面的才是很可以的
插入数据
从这里开始就可以变得难一些了,我们需要考虑的事情就有点多了.
这里面存在一个难点,就是我们找到了一个可以插入的玩位置,如何确定父节点,所以这里需要找一个节点记录夫节点,这样才可以.
bool
insert(
const
T
&
val)
{
// 头一次 插入
if (
_root
==
nullptr)
{
_root
=
new
Node(
val);
return
true;
}
Node
*
parent
=
nullptr;
Node
*
cur
=
_root;
while (
cur
!=
nullptr)
{
if (
val
>
cur
->
_key)
{
parent
=
cur;
cur
=
cur
->
right;
}
else
if (
val
<
cur
->
_key)
{
parent
=
cur;
cur
=
cur
->
left;
}
else
{
// 这里 我们不允许 插入相同的 值
return
false;
}
}
// 判断一些插入 左子树 还是 右子树
if (
parent
->
_key
<
val)
parent
->
right
=
new
Node(
val);
else
parent
->
left
=
new
Node(
val);
return
true;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
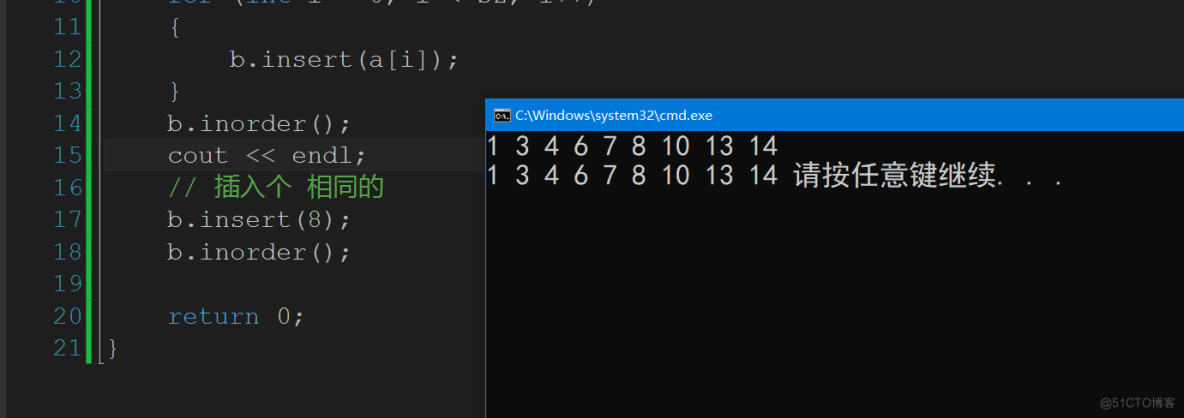
我们先来验证一下,看看是不是插入成功了.
int
main()
{
BSTree
<
int
>
b;
int
a[]
= {
8,
3,
1,
10,
6,
4,
7,
14,
13 };
int
sz
=
sizeof(
a)
/
sizeof(
int);
for (
int
i
=
0;
i
<
sz;
i
++)
{
b.
insert(
a[
i]);
}
b.
inorder();
cout
<<
endl;
// 插入个 相同的
b.
insert(
8);
b.
inorder();
return
0;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
递归版本
这里面递归版本应该是比较难理解,准确说递归的都很难,我们这里来解释一下吧,这里你就会发现引用的好处.
public:
bool
insertR(
const
T
&
val)
{
return
_insertR(
_root,
val);
}
private:
bool
_insertR(
Node
*&
root,
const
T
&
val)
{
if (
root
==
nullptr)
{
root
=
new
Node(
val);
}
//
if (
val
>
root
->
_key)
_insertR(
root
->
right,
val);
else
if (
val
<
root
->
_key)
_insertR(
root
->
left,
val);
else
return
false;
return
true;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
我来解释一下这个函数,主要是这个递归函数.
首先,我们先看最简单的一种情况,第一次插入数据,那么我们要修改的是_root,递归函数函数里面存在的是root,不过不要担心,要知道,我们传入的是参数的别名,所以这里我们可以直接修改.
那么现在就存在下面的一个问题了,我们在其他位置插入数据,我们看一下过程
我们依次递归,直到我们编译器找到root为空时,这样就可以直接赋值,因为root是引用,而且这个引用还确定;了我们插入的是左子树还是右子树.
这里也来验证一下.
删除数据
删除数据是这里面最难的,我们先来啃一下这个骨头.删除数据分为下面四种情况,其中有着一种情况可以归到其他两种里面的任何一种.
记住,即使是删除节点后,这棵二叉树也应该是二叉搜索树.
- 删除节点 无左子树 和 右子树
- 删除节点 无左子树
- 删除节点 无右子树
- 删除节点 存在左子树 和 右子树
这里面也就第四种情况比较困难,第一中可以归纳到下面的两种的任意一种,这里我们归纳到了无左子树这种了.我们先解决前三中种情况.
先把函数的框架搭出来,我们需要一个节点记录要删除节点的父亲节点.
bool
erase(
const
T
&
val)
{
if (
_root
==
nullptr)
return
false;
Node
*
parent
=
nullptr;
Node
*
cur
=
_root;
while (
cur
!=
nullptr)
{
if (
val
>
cur
->
_key)
{
parent
=
cur;
cur
=
cur
->
right;
}
else
if (
val
<
cur
->
_key)
{
parent
=
cur;
cur
=
cur
->
left;
}
// 找到了 要删除的节点了
else
{
// 左子树 为空 或者 左子树 和 右子树 都为空
if (
cur
->
left
==
nullptr)
{
}
// cur 一个 右为空
else
if (
cur
->
right
==
nullptr)
{
}
// 左子树 和 右子树 都为空
else
{
}
}
}
return
false;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
没有左子树 或者 没有 左子树 和 右子树
// cur 左 右 左一个 为空 或者 都为空
if (
cur
->
left
==
nullptr)
{
// 首先 要判断 删除的节点是 头节点 这样 parent = nullptr
if (
cur
==
_root)
{
_root
=
cur
->
left;
delete
cur;
return
true;
}
// 判断 要删除的 节点 是 父节点的左子树 还是 右子树
if (
cur
==
parent
->
left)
{
// 主意 这里不能置为空 你不确定 cur 有没有 右子树
parent
->
left
=
cur
->
right;
}
else
{
parent
->
right
=
cur
->
right;
}
delete
cur;
return
true;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
存在 右子树 但是 不存在 左子树
else
if (
cur
->
right
==
nullptr)
{
// 还是 要判断的
if (
cur
==
_root)
{
_root
=
cur
->
right;
delete
cur;
return
true;
}
if (
cur
==
parent
->
left)
{
parent
->
left
=
cur
->
right;
}
else
{
parent
->
right
=
cur
->
right;
}
delete
cur;
return
true;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
既存在左子树又存在右子树,这个情况是二叉搜索树中最难的了,我们需要现象如何来删除这个节点.这里存在两个方法
- 找到要删除节点中左子树 中最大值的节点 ,交换节点的值 删除它
- 找到要删除节点中右子树 中最小值的节点 ,交换节点的值 删除它
这样我们就可以删除我们想要的值了.我们这里是找右节点中最小的值.
else
{
Node
*
minParent
=
cur;
Node
*
minRight
=
cur
->
right;
while (
minRight
->
left)
{
minParent
=
minRight;
minRight
=
minRight
->
left;
}
// 交换 或者 直接覆盖
std::swap(
minRight
->
_key,
cur
->
_key);
// 删除 所在的节点
if (
minParent
->
left
==
minRight)
{
minParent
->
left
=
minRight
->
right;
}
else
{
minParent
->
right
=
minRight
->
right;
}
delete
minRight;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
到这里我们就把删除给写好了,.我们先来测试一下,后面再说递归的版本.
int
main()
{
BSTree
<
int
>
b;
int
a[]
= {
8,
3,
1,
10,
6,
4,
7,
14,
13 };
int
sz
=
sizeof(
a)
/
sizeof(
int);
for (
int
i
=
0;
i
<
sz;
i
++)
{
b.
insertR(
a[
i]);
}
b.
inorder();
for (
int
e :
a)
{
b.
erase(
e);
}
b.
inorder();
return
0;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
递归版本
这里面也是一个困难啊,和上面一个递归一样,都使用的引用.这里还需要分为三种情况,不过前提是需要找到删除的节点.
这里面还是分为四种情况,我们直接说吧,都挺简单的,这里面我们可以直接给root赋值原因还是在于我们传入的是引用,这个引用就是父节点的左子树或者右子树,而且还只能唯一确定.
bool
_eraseR(
Node
*&
root,
const
T
&
val)
{
if (
root
==
nullptr)
{
return
false;
}
if (
root
->
_key
>
val)
{
_eraseR(
root
->
left,
val);
}
else
if (
root
->
_key
<
val)
{
_eraseR(
root
->
right,
val);
}
// 找到了
else
{
// 还分为 四种 情况
if (
root
->
left
==
nullptr)
{
Node
*
cur
=
root;
root
=
root
->
right;
delete
cur;
}
else
if (
root
->
right
==
nullptr)
{
Node
*
cur
=
root;
root
=
root
->
left;
delete
cur;
}
else
{
Node
*
minRight
=
root
->
right;
while (
minRight
->
left
!=
nullptr)
{
minRight
=
minRight
->
left;
}
// 这是一个好东西
swap(
root
->
_key,
minRight
->
_key);
// 这里 递归 删除 要知道 现在 val所在的节点 一定是 没有左子树的
return
_eraseR(
root
->
right,
val);
}
return
true;
}
return
false;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
我们也来验证一下吧.
int
main()
{
BSTree
<
int
>
b;
int
a[]
= {
8,
3,
1,
10,
6,
4,
7,
14,
13 };
int
sz
=
sizeof(
a)
/
sizeof(
int);
for (
int
i
=
0;
i
<
sz;
i
++)
{
b.
insertR(
a[
i]);
}
b.
inorder();
for (
int
e :
a)
{
b.
eraseR(
e);
b.
inorder();
cout
<<
endl;
}
b.
inorder();
return
0;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
查找数据
这里的就简单了,我这里也不啰嗦了,直接上代码.
Node
*
find(
const
T
&
key)
{
if (
_root
==
nullptr)
return
nullptr;
Node
*
cur
=
_root;
while (
cur)
{
if (
key
>
cur
->
_key)
{
cur
=
cur
->
right;
}
else
if (
key
<
cur
->
_key)
{
cur
=
cur
->
left;
}
else
{
return
cur;
}
}
return
nullptr;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
如果你要是这们写这就有问题了,我们拿到了指针,这就意味者我们可以修改节点里面的值,那就麻烦了,因为你不确定你修改过的值还是否构成搜索二叉树.
我们这里改一下节点的值,用const修饰.
但是还是存在问题的 ,想一想,我们在删除数据的时候交换了节点的值,这就出现了另一个问题,因为const修饰的常量就不能被修改了,这里我就不给出解决的代码了,只说下思路.我们还是用const修饰,交换节点的值改成交换节点,当然,他们原本的指向也应该合理的变化.
递归写法
public:
Node
*
findR(
const
T
&
key)
{
return
_findR(
_root,
key);
}
private:
Node
*
_findR(
Node
*
root,
const
T
&
key)
{
if (
root
==
nullptr)
return
nullptr;
if (
key
>
root
->
_key)
return
_findR(
root
->
right,
key);
else
if (
key
<
root
->
_key)
return
_findR(
root
->
left,
key);
else
return
root;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
完善一下二叉树搜索树
我们把它的拷贝构造等几个函数给写一下就可以了,这脸都是挺简单的,而且说实话我们也不是太常用.
拷贝构造
我们完善一下代码就可以了
private:
Node
*
CopyTree(
Node
*
root)
{
if (
root
==
nullptr)
{
return
nullptr;
}
Node
*
copyNode
=
new
Node(
root
->
_key);
copyNode
->
left
=
CopyTree(
root
->
left);
copyNode
->
right
=
CopyTree(
root
->
right);
return
copyNode;
}
public:
BSTree(
const
BSTree
<
T
>&
b)
:
_root(
nullptr)
{
_root
=
CopyTree(
b.
_root);
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
析构函数
operator=
我们这里来测试一下就好了,没有什么可以谈的.
int
main()
{
BSTree
<
int
>
b1;
int
a[]
= {
8,
3,
1,
10,
6,
4,
7,
14,
13 };
int
sz
=
sizeof(
a)
/
sizeof(
int);
for (
int
i
=
0;
i
<
sz;
i
++)
{
b1.
insertR(
a[
i]);
}
BSTree
<
int
>
b2(
b1);
// 拷贝构造
BSTree
<
int
>
b3;
b3
=
b1;
// operater =
b2.
inorder();
cout
<<
endl;
b3.
inorder();
cout
<<
endl;
return
0;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
应用
相比较其他的,我这里更想谈谈它的应用.
K模型
K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值 .我们的英语字典就可以,我们可以把英语字典的词放在一个二叉搜索树中,这样就可以检擦一个单词是不是拼写正确.我们上面实现的就是这个模型,后面的set也是这个模型.
KV模型
每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。该种方式在现实生活中非常常见： 比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文<word, chinese>就构成一种键值对 .后面的map用这个模型.
边栏推荐
- 为什么数据需要序列化
- Public Key Retrieval is not allowed报错解决方案
- [AGC] Quality Service 1 - Example of Crash Service
- Sparse-PointNet: See Further in Autonomous Vehicles 论文笔记
- The service already exists!解决办法
- 【AGC】质量服务1-崩溃服务示例
- Placement Rules usage documentation
- 谷歌工程师『代码补全』工具；『Transformers NLP』随书代码；FastAPI开发模板；PyTorch模型加速工具；前沿论文 | ShowMeAI资讯日报
- How to use Redis for distributed applications in Golang
- 【C语言】指针和数组的深入理解（第二期）
猜你喜欢
![[AGC] Quality Service 2 - Performance Management Example](/img/09/4a7c57f5aa651e4ac58d1e6d73afe6.png)
随机推荐
Recent learning defragmentation (24)
Array element inverse
70 lines of code, a desktop automatic translation artifact
影像信息提取DEM
字符串加千分位符与递归数组求和
MySql 和 PostgreSQL 数据库 根据一张表update另一张表数据
RobotStudio实现喷漆、打磨等功能（曲面路径生成与仿真）
详解最实用的几种dll注入方式
游戏窗口化的逆向分析
Horizontal Pod Autoscaler（HPA）
node.js中怎么连接redis?
php如何查询字符串出现位置
23. 请你谈谈关于IO同步、异步、阻塞、非阻塞的区别
arcpy使用教程
华为ADS获取转化跟踪参数报错：getInstallReferrer IOException: getInstallReferrer not found installreferrer
How to use Redis for distributed applications in Golang
Overview of TiDB Tool Functions
【SOC】经典输出hello world
PyQt5快速开发与实战 9.2 数据库处理
几种常见的存储器