当前位置:网站首页>Self attention and multi head attention
Self attention and multi head attention
2022-06-10 20:50:00 【Binary artificial intelligence】
List of articles
We met before A general attention model . This article will introduce self attention and multi attention , For the follow-up introduction Transformer Do matting .
Self attention
If attention in the attention model is calculated completely based on eigenvectors , Then call this kind of attention self attention :

Picture changed from :[1]
for example , We can use the weight matrix W K ∈ R d k × d f \boldsymbol{W}_K∈\mathbb{R}^{d_k×d_f} WK∈Rdk×df、 W V ∈ R d v × d f \boldsymbol{W}_V∈\mathbb{R}^{d_v×d_f} WV∈Rdv×df and W Q ∈ R d q × d f \boldsymbol{W}_{Q} \in \mathbb{R}^{d_{q} \times d_{f}} WQ∈Rdq×df For the characteristic matrix F = [ f 1 , … , f n f ] ∈ R d f × n f \boldsymbol{F}=[\boldsymbol{f}_{1}, \ldots, \boldsymbol{f}_{n_{f}}] \in \mathbb{R}^{d_{f}\times n_f} F=[f1,…,fnf]∈Rdf×nf Make a linear transformation , obtain
key (Key) matrix
K = W K F = W K [ f 1 , … , f n f ] = [ k 1 , … , k n f ] ∈ R d k × n f \begin{aligned} \boldsymbol{K}&=\boldsymbol{W}_{K}\boldsymbol{F}\\ &=\boldsymbol{W}_{K}[\boldsymbol{f}_{1}, \ldots, \boldsymbol{f}_{n_{f}}]\\ &=\left[\boldsymbol{k}_{1}, \ldots, \boldsymbol{k}_{n_{f}}\right] \in \mathbb{R}^{d_{k} \times n_{f}} \end{aligned} K=WKF=WK[f1,…,fnf]=[k1,…,knf]∈Rdk×nf
value (Value) matrix
V = W V F = W V [ f 1 , … , f n f ] = [ v 1 , … , v n f ] ∈ R d v × n f \begin{aligned} \boldsymbol{V}&=\boldsymbol{W}_{V}\boldsymbol{F}\\ &=\boldsymbol{W}_{V}[\boldsymbol{f}_{1}, \ldots, \boldsymbol{f}_{n_{f}}]\\ &=\left[\boldsymbol{v}_{1}, \ldots, \boldsymbol{v}_{n_{f}}\right] \in \mathbb{R}^{d_{v} \times n_{f}} \end{aligned} V=WVF=WV[f1,…,fnf]=[v1,…,vnf]∈Rdv×nf
Inquire about (Query) matrix
Q = W Q F = W Q [ f 1 , … , f n f ] = [ q 1 , … , q n f ] ∈ R d q × n f \begin{aligned} \boldsymbol{Q}&=\boldsymbol{W}_{Q}\boldsymbol{F}\\ &=\boldsymbol{W}_{Q}[\boldsymbol{f}_{1}, \ldots, \boldsymbol{f}_{n_{f}}]\\ &=\left[\boldsymbol{q}_{1}, \ldots, \boldsymbol{q}_{n_{f}}\right] \in \mathbb{R}^{d_{q} \times n_{f}} \end{aligned} Q=WQF=WQ[f1,…,fnf]=[q1,…,qnf]∈Rdq×nf
Q \boldsymbol{Q} Q Each column of q i \boldsymbol{q}_i qi Are used as queries for the attention model . When using query vectors q i \boldsymbol{q}_i qi When calculating attention , Generated context vector c i \boldsymbol{c}_i ci Will summarize the eigenvectors in the query q i \boldsymbol{q}_i qi For important information .
First , Query pair q i , i = 1 , 2 , . . . , n f \boldsymbol{q}_i,i=1,2,...,n_f qi,i=1,2,...,nf Calculate key vector k j \boldsymbol{k}_{j} kj The attention score of :
e i , j 1 × 1 = score ( q i d q × 1 , k j d k × 1 ) , j = 1 , 2 , . . . , n f \underset{1 \times 1}{e_{i,j}}=\operatorname{score}\left(\underset{d_{q} \times 1}{\boldsymbol{q}_i}, \underset{d_{k} \times 1}{\boldsymbol{k}_{j}}\right),j=1,2,...,n_f 1×1ei,j=score(dq×1qi,dk×1kj),j=1,2,...,nf
Inquire about q i \boldsymbol{q}_i qi Indicates a request for information . Attention score e i , j e_{i,j} ei,j Indicates that according to the query q i \boldsymbol{q}_i qi, Bond vector k j \boldsymbol{k}_j kj How important is the information contained in . Calculate the score of each value vector , Get information about the query q i \boldsymbol{q}_i qi Attention score vector :
e i = [ e i 1 , e i 2 , . . . , e i , n f ] T \boldsymbol{e_i}=[e_{i1},e_{i2},...,e_{i,n_f}]^T ei=[ei1,ei2,...,ei,nf]T
then , Use the alignment function align ( ) \operatorname{align}() align() Align :
a i , j 1 × 1 = align ( e i , j ; 1 × 1 e i n f × 1 ) , j = 1 , 2 , . . . , n f \underset{1 \times 1}{a_{i,j}}=\operatorname{align}\left(\underset{1 \times 1}{e_{i,j} ;} \underset{n_{f} \times 1}{\boldsymbol{e_i}}\right),j=1,2,...,n_f 1×1ai,j=align(1×1ei,j;nf×1ei),j=1,2,...,nf
Get the attention weight vector : a i = [ a i , 1 , a i , 2 , . . . , a i , n f ] T \boldsymbol{a}_i=[a_{i,1},a_{i,2},...,a_{i,n_f}]^T ai=[ai,1,ai,2,...,ai,nf]T.
Finally, the context vector is calculated :
c i d v × 1 = ∑ j = 1 n f a i , j 1 × 1 × v j d v × 1 \underset{d_{v} \times 1}{\boldsymbol{c}_i}=\sum_{j=1}^{n_{f}}\underset{1\times 1} {a_{i,j}} \times \underset{d_v\times 1}{\boldsymbol{v}_{j}} dv×1ci=j=1∑nf1×1ai,j×dv×1vj
Summarize the above steps , The self attention calculation expression is :
c i = self-att ( q i , K , V ) ∈ R d v \boldsymbol{c}_i=\text { self-att }(\boldsymbol{q}_i, \boldsymbol{K}, \boldsymbol{V})\in \mathbb{R}^{d_v} ci= self-att (qi,K,V)∈Rdv
because q i = W Q f i \boldsymbol{q}_i=\boldsymbol{W}_Q\boldsymbol{f}_i qi=WQfi, So we can say that the context vector c i \boldsymbol{c}_i ci Include all eigenvectors ( Include f i \boldsymbol{f}_i fi) For a particular eigenvector f i \boldsymbol{f}_i fi For important information . for example , For language , This means that self attention can extract the relationship between word features ( Verbs and nouns ; Pronouns and nouns, etc ), If f i \boldsymbol{f}_i fi Is the eigenvector of a word , Then self attention can be calculated from other words f i \boldsymbol{f}_i fi For important information . For the image , Self attention can get the relationship between the features of each image region .
Calculation Q \boldsymbol{Q} Q Context vectors for all query vectors in , Get the output from the attention layer :
C = self-att ( Q , K , V ) = [ c 1 , c 2 , . . . , c n f ] ∈ R d v × n f \boldsymbol{C}=\text { self-att }(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=[\boldsymbol{c}_1,\boldsymbol{c}_2,...,\boldsymbol{c}_{n_f}]\in \mathbb{R}^{d_{v}\times n_f} C= self-att (Q,K,V)=[c1,c2,...,cnf]∈Rdv×nf
Long attention

Multi head attention works by using multiple different versions of the same query to implement multiple attention modules in parallel . The idea is to use different weight matrices to query q \boldsymbol{q} q Get multiple queries by linear transformation . Each newly formed query essentially requires different types of relevant information , This allows the attention model to introduce more information into the context vector computation .
Bulls pay attention to d d d Each header has its own multiple query vectors 、 Key matrix and value matrix : q ( l ) , K ( l ) \boldsymbol{q}^{(l)}, \boldsymbol{K}^{(l)} q(l),K(l) and V ( l ) \boldsymbol{V}^{(l)} V(l), l = 1 , … , d l=1, \ldots, d l=1,…,d.
Inquire about q ( l ) \boldsymbol{q}^{(l)} q(l) By the original query q \boldsymbol{q} q After linear transformation, we get , and K ( l ) \boldsymbol{K}^{(l)} K(l) and V ( l ) \boldsymbol{V}^{(l)} V(l) It is F \boldsymbol{F} F After linear transformation, we get . Each attention head has its own learnable weight matrix W q ( l ) 、 W K ( l ) and W V ( l ) \boldsymbol{W}^{(l)}_q、\boldsymbol{W}^{(l)}_K and \boldsymbol{W}^{(l)}_V Wq(l)、WK(l) and WV(l). The first l l l Head of the query 、 The keys and values are calculated as follows :
q ( l ) d q × 1 = W q ( l ) d q × d q × q d q × 1 , \underset{d_{q} \times 1}{\boldsymbol{q}^{(l)}}=\underset{d_{q} \times d_{q}}{\boldsymbol{W}_{q}^{(l)}} \times \underset{d_{q} \times 1}{\boldsymbol{q}}, dq×1q(l)=dq×dqWq(l)×dq×1q,
K ( l ) d k × n f = W K ( l ) d k × d f × F d f × n f \underset{d_{k} \times n_{f}}{\boldsymbol{K}^{(l)}}=\underset{d_{k} \times d_{f}}{\boldsymbol{W}_K^{(l)}} \times \underset{d_{f} \times n_{f}}{\boldsymbol{F}} dk×nfK(l)=dk×dfWK(l)×df×nfF
V ( l ) d v × n f = W V ( l ) d v × d f × F d f × n f \underset{d_{v} \times n_{f}}{\boldsymbol{V}^{(l)}}=\underset{d_{v} \times d_{f}}{\boldsymbol{W}_V^{(l)}} \times \underset{d_{f} \times n_{f}}{\boldsymbol{F}} dv×nfV(l)=dv×dfWV(l)×df×nfF
Each header creates its own pair of queries q \boldsymbol{q} q And input matrix F \boldsymbol{F} F It means , This allows the model to learn more information . for example , When training language models , An attentional head can learn to pay attention to certain verbs ( For example, walking 、 Drive 、 Buy ) And noun ( for example , Student 、 automobile 、 Apple ) The relationship between , The other attentional head learns to focus on pronouns ( for example , He 、 she 、it) The relationship with nouns .
Each head will also create its own attention score vector e i ( l ) = [ e i , 1 ( l ) , … , e i , n f ( l ) ] T ∈ R n f \boldsymbol{e}_i^{(l)}=\left[e_{i,1}^{(l)}, \ldots, e_{i,n_{f}}^{(l)}\right]^T \in \mathbb{R}^{n_{f}} ei(l)=[ei,1(l),…,ei,nf(l)]T∈Rnf, And the corresponding attention weight vector a i ( l ) = [ a i , 1 ( l ) , … , a i , n f ( l ) ] T ∈ R n f \boldsymbol{a}_i^{(l)}=\left[a_{i,1}^{(l)}, \ldots, a_{i,n_{f}}^{(l)}\right]^T \in \mathbb{R}^{n_{f}} ai(l)=[ai,1(l),…,ai,nf(l)]T∈Rnf
then , Each header generates its own context vector c i ( l ) ∈ R d v \boldsymbol{c}_i^{(l)}\in \mathbb{R}^{d_{v}} ci(l)∈Rdv, As shown below :
c i ( l ) d v × 1 = ∑ j = 1 n f a i , j ( l ) 1 × 1 × v j ( l ) d v × 1 \underset{d_{v} \times 1}{\boldsymbol{c}_i^{(l)}}=\sum_{j=1}^{n_f} \underset{1\times 1}{a_{i,j}^{(l)}}\times \underset{d_{v}\times 1}{\boldsymbol{v}_j^{(l)}} dv×1ci(l)=j=1∑nf1×1ai,j(l)×dv×1vj(l)
Our goal is still to create a context vector as the output of the attention model . therefore , The context vectors generated by each attention head are connected into a vector . then , Use the weight matrix W O ∈ R d c × d v d \boldsymbol{W}_{O} \in \mathbb{R}^{d_{c} \times d_{v} d} WO∈Rdc×dvd Perform a linear transformation on it :
c i d c × 1 = W O d c × d v d × concat ( c i ( 1 ) d v × 1 ; … ; c i ( d ) d v × 1 ) \underset{d_{c} \times 1}{\boldsymbol{c}_i}=\underset{d_{c} \times d_{v} d}{\boldsymbol{W}_{O}} \times \operatorname{concat}\left(\underset{d_v \times 1}{\boldsymbol{c}_i^{(1)}} ; \ldots; \underset{d_v \times 1}{\boldsymbol{c}_i^{(d)}} \right) dc×1ci=dc×dvdWO×concat(dv×1ci(1);…;dv×1ci(d))
This ensures that the final context vector c i ∈ R d c \boldsymbol{c}_i\in\mathbb{R}^{d_c} ci∈Rdc Conform to the target dimension
Reference resources :
[1] A General Survey on Attention Mechanisms in Deep Learning https://arxiv.org/pdf/2203.14263v1.pdf

边栏推荐
- redis设置密码命令(临时密码)
- Fs4521 constant voltage linear charging IC
- 手写代码 bind
- Why do some web page style attributes need a colon ":" and some do not?
- The old programmer said: stop translating the world, developers should return to programming
- 在阿里云国际上使用 OSS 和 CDN 部署静态网站
- Kcon 2022 topic public selection is hot! Don't miss the topic of "favorite"
- pdf. Js----- JS parse PDF file to realize preview, and obtain the contents in PDF file (in array form)
- 【录入课本latex记录】
- Redis cluster form - sentry mode cluster and high availability mode cluster - redis learning notes 003
猜你喜欢

传音 Infinix 新机现身谷歌产品库,TECNO CAMON 19 预装 Android 13
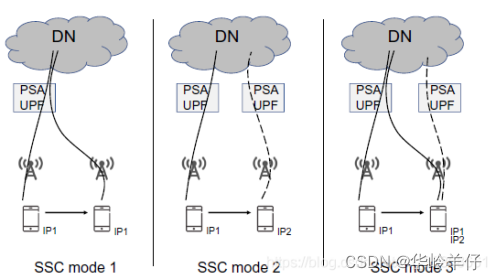
PDU session flow

CVPR 2022 Tsinghua University proposed unsupervised domain generalization (UDG)

暗黑破坏神不朽数据库怎么用 暗黑破坏神手游不朽数据库使用方法

pytorch深度学习——卷积操作以及代码示例

Microsoft Word tutorial, how to change page orientation and add borders to pages in word?

Connexion MySQL errorcode 1129, State hy000, Host 'xxx' is Blocked because of many Connection Errors

Four methods to obtain the position index of the first n values of the maximum and minimum values in the list
![JS basic and frequently asked interview questions [] = =! [] result is true, [] = = [] result is false detailed explanation](/img/42/bcda46a9297a544b44fea31be3f686.png)
JS basic and frequently asked interview questions [] = =! [] result is true, [] = = [] result is false detailed explanation
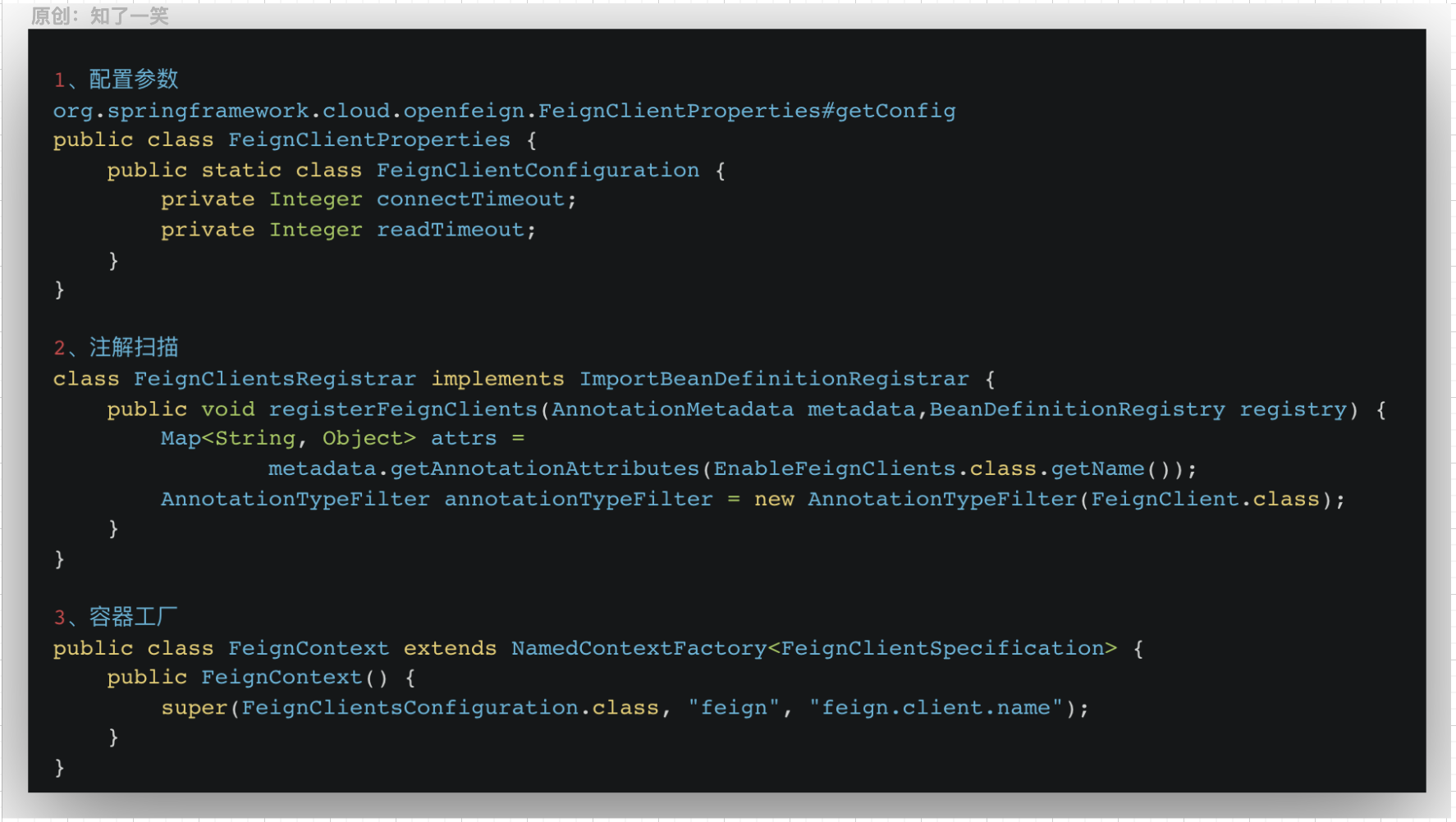
服务管理与通信,基础原理分析
随机推荐
8.4v dual lithium battery professional charging IC (fs4062a)
Mysql database foundation
When can Flink support the SQL client mode? When can I specify the applicati for submitting tasks to yarn
Hm3416h buck IC chip pwm/pfm controls DC-DC buck converter
Microsoft Word 教程,如何在 Word 中更改页面方向、为页面添加边框?
C语言 浮点数 储存形式
Qualcomm qc2.0 fast charging intelligent identification IC fp6719
[observation] shengteng Zhixing: scene driven, innovation first, press the "acceleration key" for Intelligent Transportation
JD released ted-q, a large-scale and distributed quantum machine learning platform based on tensor network acceleration
mixin--混入
How to realize face verification quickly and accurately?
魔塔类游戏实现源码及关卡生成
The excess part of the table setting is hidden. Move the mouse to display all
Jiangbolong forestee xp2000 PCIe 4.0 SSD multi encryption function, locking data security
LeetCode:1037. 有效的回旋镖————简单
Mixin -- mixed
"Bug" problem analysisruntimeerror:which is output 0 of resubackward0
KCon 2022 议题大众评选火热进行中!不要错过“心仪”的议题哦~
Key points of lldp protocol preparation
详解三级缓存解决循环依赖