当前位置:网站首页>矩阵数学原理
矩阵数学原理
2022-08-04 23:36:00 【王不偏】
开篇名义1:
左乘一个矩阵就代表对右边的向量做一次变换,向量代表的是一条有方向的直线,变换的结果其实就是对这条直线进行各种运动,包括:平移、旋转、伸缩、投影(高维到低维)、映射等,其中,映射是对一个向量作升维或降维(也可以在同一空间中)的操作 Rn→ Rm,所以广义上,映射的意思等同于变换。
另外一个经常提到的词是“线性变换”,线性变换保证了输入的直线(向量)在变换过程中不会产生弯曲,即输入是直线,输出也是直线。因为 矩阵变换都是线性变换,所以我们这里说的“变换”其实就是“线性变换”
开篇名义2:
在各种变换中,有一种变换拥有良好的特性——它能使变换后的向量长度,向量之间的内积、距离、夹角等很多性质都不变,这种变换,我们称为正交变换,用于实施这种变换的矩阵,我们称为正交矩阵,这种变换的特性,我们称为正交变换的不变性。
假如有m个向量,我们把向量都看作点,那么这m点就会构成一个具有一定几何结构的空间(图形),我们对这m个点进行正交变换,其结果直观来说就是,正交变换不会对图形进行拉伸、压缩,它能够使变换后的图形保持原来图形的几何形状,如下图所示,ABC构成的空间正交变换到A’B’C’,其大小和形状都不会改变。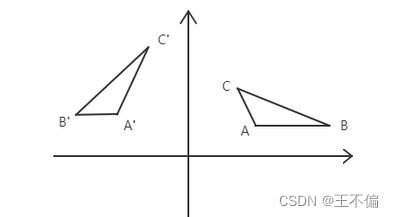
上面的正交变换是从变换的结果来进行直观的解释,可以看到这种变换拥有良好的性质——能够保持空间的不变性,保证不会对原空间产生压缩拉伸,往深了说,就是这种变换不会损失信息,因为它保持了原空间的内部结构,这在工程上是很有用的。
原文链接:https://blog.csdn.net/MoreAction_/article/details/105442932
1 .线性方程和正交化的几何原理:
参考文章链接:https://www.cnblogs.com/ailitao/p/11047275.html

Gram-schmidt正交法的本质是减去在其他基上的投影,那么剩下的就是垂直部分的分量(垂直就是正交的意思)

同理,对于向量间的夹角<>,由于长度和内积不变,所以夹角不变
同理,还可证得向量间的距离不变
由于长度、夹角和距离都不变,所以正交变换能够保持空间的几何形状。

2.QR分解:
A是对称矩阵和非对称矩阵都适用。
A=QR;
QR分解是将矩阵分解成一个正交矩阵Q和上三角矩阵R,所以称为QR分解法。该算法对对称矩阵和非对称矩阵都适用。
3. cholesky分解原理:
前提:A ∈ R (n × n)是对称正定矩阵,
则有:A= L*L^T;
L是一个对角元全为正数的下三角矩阵 L ∈ R (n × n) ,
Cholesky分解把矩阵分解为一个下三角矩阵以及它的共轭转置矩阵的乘积(那实数界来类比的话,此分解就好像求平方根)。与一般的矩阵分解求解方程的方法比较,Cholesky分解效率很高。
关于LU分解,Cholesky分解,QR分解,SVD分解,Jordan分解分解的汇总:https://blog.csdn.net/mucai1/article/details/85242098
边栏推荐
- 如何根据地址获取函数名
- 为何越来越多人选择进入软件测试行业?深度剖析软件测试的优势...
- Day118. Shangyitong: order list, details, payment
- 使用代理对象执行实现类目标方法异常
- Shell expect real cases
- 从单体架构迁移到 CQRS 后,我觉得 DDD 并不可怕
- KT148A电子语音芯片ic方案适用的场景以及常见产品类型
- Bidding Announcement | Operation and Maintenance Project of Haina Baichuang Official Account
- typeScript-promise
- Pytorch分布式训练/多卡/多GPU训练DDP的torch.distributed.launch和torchrun
猜你喜欢
随机推荐
加解密在线工具和进制转化在线工具
I was rejected by the leader for a salary increase, and my anger rose by 9.5K after switching jobs. This is my mental journey
MYS-6ULX-IOT 开发板测评——使用 Yocto 添加软件包
Bidding Announcement | Operation and Maintenance Project of Haina Baichuang Official Account
KT148A电子语音芯片ic方案适用的场景以及常见产品类型
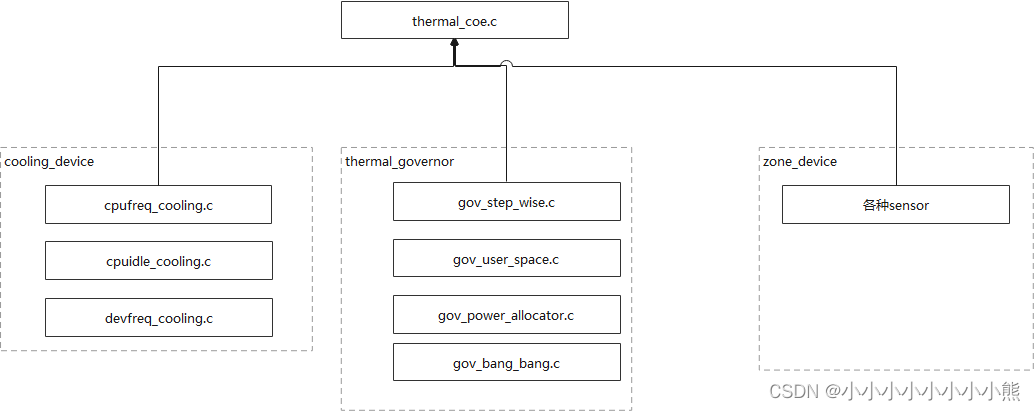
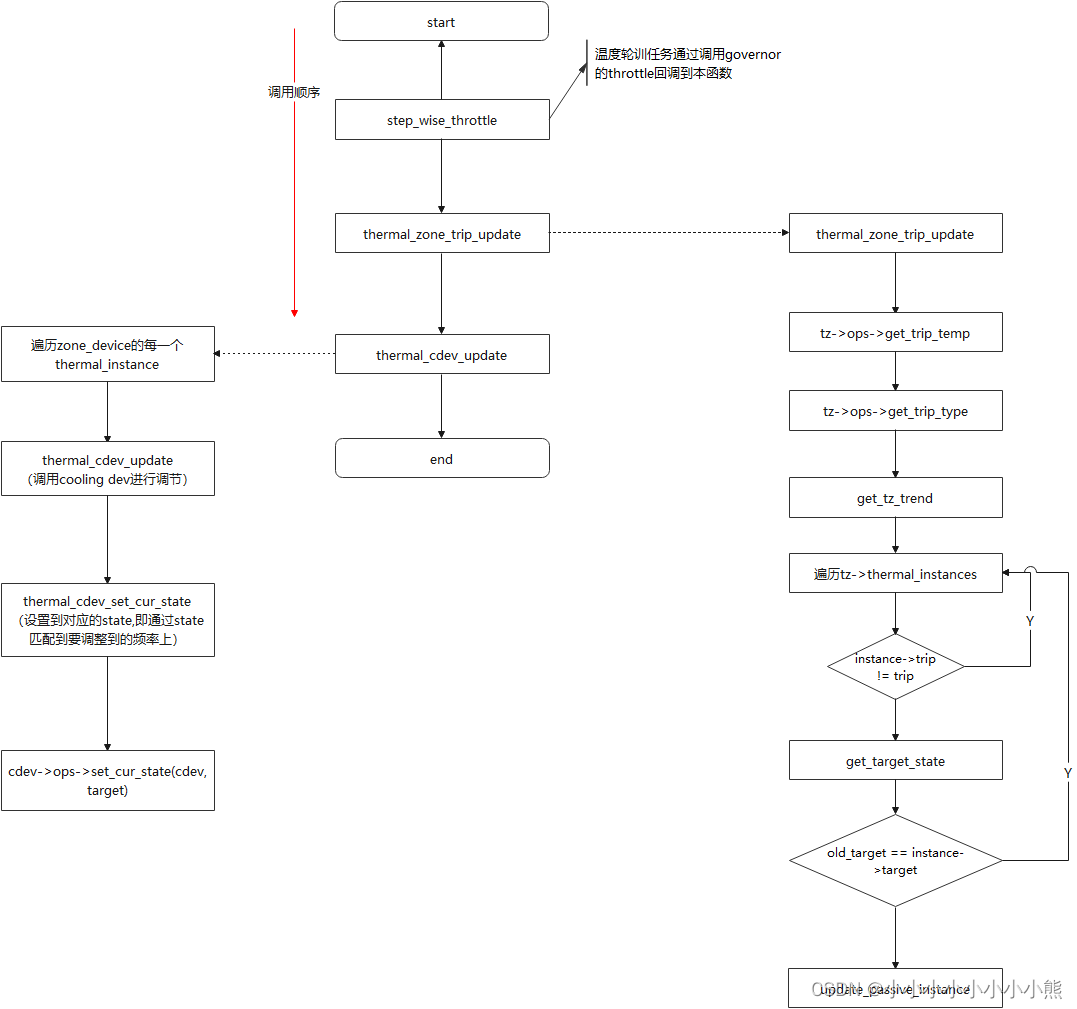
一点点读懂thermal(一)
MySQL增删改查基础
中日颜色风格
kernel问题定位手段总结
Service Mesh landing path
Controller层代码这么写,简洁又优雅!
The role of @Async annotation and how to implement asynchronous listening mechanism
Day118.尚医通:订单列表、详情、支付
~ hand AHB - APB Bridge 】 【 AMBA AHB bus
对写作的一些感悟
自从新来了个字节20K出来的,就见识到了什么是天花板
Community Sharing|Tencent Overseas Games builds game security operation capabilities based on JumpServer
测试技术:关于上下文驱动测试的总结
npm基本操作及命令详解
Flutter启动流程(Skia引擎)介绍与使用