当前位置:网站首页>Concise Notes on Integrals - Types of Curve Integrals of the Second Kind
Concise Notes on Integrals - Types of Curve Integrals of the Second Kind
2022-07-30 09:20:00 【The stars in accordance with the month】
Types of curve integrals of the second kind
一、Classification of curve integrals of the second kind
01 Plane curve integrals of the second kind
02 Curve integrals of the second kind in space
二、A representation of the curve integral of the second kind
00 Preparation for analysis

d s ⋅ cos α = ∣ P T ∣ cos α = ∣ P Q ∣ = d x ds\cdot\cos\alpha=|PT|\cos\alpha=|PQ|=dx ds⋅cosα=∣PT∣cosα=∣PQ∣=dx, d s = tan 2 α + 1 ⋅ d x ds=\sqrt{\tan^2\alpha+1}\cdot dx ds=tan2α+1⋅dx
a ⃗ = { x 1 , y 1 , z 1 } \vec{a}=\{x_1,y_1,z_1\} a={ x1,y1,z1}, x 1 = a ⃗ ⋅ i ⃗ = ∣ a ⃗ ∣ cos α x_1=\vec{a}\cdot\vec{i}=|\vec{a}|\cos\alpha x1=a⋅i=∣a∣cosα,
y 1 = a ⃗ ⋅ j ⃗ = ∣ a ⃗ ∣ cos β y_1=\vec{a}\cdot\vec{j}=|\vec{a}|\cos\beta y1=a⋅j=∣a∣cosβ, z 1 = a ⃗ ⋅ k ⃗ = ∣ a ⃗ ∣ cos γ z_1=\vec{a}\cdot\vec{k}=|\vec{a}|\cos\gamma z1=a⋅k=∣a∣cosγ
01 Plane curve integrals of the second kind
一般形式: ∫ Γ A B ( A ⃗ ( P ) ⋅ T 0 ⃗ ( P ) ) d s = ∫ Γ A B ( A ⃗ ⋅ T 0 ⃗ ) d s \int_{\Gamma_{AB}}(\vec{A}(P)\cdot\vec{T^0}(P))ds=\int_{\Gamma_{AB}}(\vec{A}\cdot\vec{T^0})ds ∫ΓAB(A(P)⋅T0(P))ds=∫ΓAB(A⋅T0)ds
若 Γ A B ⊂ R 2 \Gamma_{AB}\subset\mathrm{R}^2 ΓAB⊂R2, P ( x , y ) ∈ Γ A B P(x,y)\in\Gamma_{AB} P(x,y)∈ΓAB, T ⃗ \vec{T} T Curves in the plane Γ \Gamma Γ 上点 ( x , y ) (x,y) (x,y) 处,The unit vector of the tangent T 0 ⃗ \vec{T^0} T0 与指定的方向一致.
T 0 ⃗ = { cos α , cos β } \vec{T^0}=\{\cos\alpha,\cos\beta\} T0={ cosα,cosβ} , T 0 → ⋅ d s = △ d s ⃗ = { cos α , cos β } = { d x , d y } \overrightarrow{T_0}\cdot ds\stackrel{\triangle}{=}d\vec{s}=\{\cos\alpha,\cos\beta\}=\{dx,dy\} T0⋅ds=△ds={ cosα,cosβ}={ dx,dy} , A ⃗ ( x , y ) = { P ( x , y ) , Q ( x , y ) } \vec{A}(x,y)=\{P(x,y),Q(x,y)\} A(x,y)={ P(x,y),Q(x,y)}
① ∫ Γ A B ( A ⃗ ⋅ T 0 ⃗ ) d s ② = ∫ Γ A B A ⃗ ⋅ d s ⃗ ③ = ∫ Γ A B ( P ( x , y ) cos α + Q ( x , y ) cos β ) d s = ∫ Γ A B ( P cos α + Q cos β ) d s ④ = ∫ Γ A B P ( x , y ) d x + Q ( x , y ) d y = ∫ Γ A B P d x + Q d y ( 用得较多 ) ⑤ = ∫ Γ A B P ( x , y ) d x + ∫ Γ A B Q ( x , y ) d y \begin{aligned} ①& \ \ \int_{\Gamma_{AB}}(\vec{A}\cdot\vec{T^0})ds\\ ②& \ \ =\int_{\Gamma_{AB}}\vec{A}\cdot d\vec{s}\\ ③& \ \ =\int_{\Gamma_{AB}}(P(x,y)\cos\alpha+Q(x,y)\cos\beta)ds\\ & \ \ =\int_{\Gamma_{AB}}(P\cos\alpha+Q\cos\beta)ds\\ ④& \ \ =\int_{\Gamma_{AB}}P(x,y)dx+Q(x,y)dy\\ & \ \ =\int_{\Gamma_{AB}}Pdx+Qdy\ \ \ (用得较多)\\ ⑤& \ \ =\int_{\Gamma_{AB}}P(x,y)dx+\int_{\Gamma_{AB}}Q(x,y)dy \end{aligned} ①②③④⑤ ∫ΓAB(A⋅T0)ds =∫ΓABA⋅ds =∫ΓAB(P(x,y)cosα+Q(x,y)cosβ)ds =∫ΓAB(Pcosα+Qcosβ)ds =∫ΓABP(x,y)dx+Q(x,y)dy =∫ΓABPdx+Qdy (用得较多) =∫ΓABP(x,y)dx+∫ΓABQ(x,y)dy
02 Curve integrals of the second kind in space
一般形式: ∫ Γ A B ( A ⃗ ( P ) ⋅ T 0 ⃗ ( P ) ) d s = ∫ Γ A B ( A ⃗ ⋅ T 0 ⃗ ) d s \int_{\Gamma_{AB}}(\vec{A}(P)\cdot\vec{T^0}(P))ds=\int_{\Gamma_{AB}}(\vec{A}\cdot\vec{T^0})ds ∫ΓAB(A(P)⋅T0(P))ds=∫ΓAB(A⋅T0)ds
若 Γ A B ⊂ R 3 \Gamma_{AB}\subset\mathrm{R}^3 ΓAB⊂R3, P ( x , y , z ) ∈ Γ A B P(x,y,z)\in\Gamma_{AB} P(x,y,z)∈ΓAB, T ⃗ \vec{T} T Curves in space Γ \Gamma Γ 上点 ( x , y , z ) (x,y,z) (x,y,z) 处,
The unit vector of the tangent T 0 ⃗ = { cos α , cos β , cos γ } \vec{T^0}=\{\cos\alpha,\cos\beta,\cos\gamma\} T0={ cosα,cosβ,cosγ} 与指定的方向一致.
T 0 ⃗ = { cos α , cos β , cos γ } \vec{T^0}=\{\cos\alpha,\cos\beta,\cos\gamma\} T0={ cosα,cosβ,cosγ} , T 0 → ⋅ d s = △ d s ⃗ = { cos α , cos β , cos γ } = { d x , d y , d z } \overrightarrow{T_0}\cdot ds\stackrel{\triangle}{=}d\vec{s}=\{\cos\alpha,\cos\beta,\cos\gamma\}=\{dx,dy,dz\} T0⋅ds=△ds={ cosα,cosβ,cosγ}={ dx,dy,dz}
A ⃗ ( x , y ) = { P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) } \vec{A}(x,y)=\{P(x,y,z),Q(x,y,z),R(x,y,z)\} A(x,y)={ P(x,y,z),Q(x,y,z),R(x,y,z)}
① ∫ Γ A B ( A ⃗ ⋅ T 0 ⃗ ) d s ② = ∫ Γ A B A ⃗ ⋅ d s ⃗ ③ = ∫ Γ A B ( P ( x , y , z ) cos α + Q ( x , y , z ) cos β + R ( x , y , z ) cos γ ) d s = ∫ Γ A B ( P cos α + Q cos β + R cos γ ) d s ④ = ∫ Γ A B P ( x , y , z ) d x + Q ( x , y , z ) d y + R ( x , y , z ) d z = ∫ Γ A B P d x + Q d y + R d z ( 用得较多 ) ⑤ = ∫ Γ A B P ( x , y , z ) d x + ∫ Γ A B Q ( x , y , z ) d y + ∫ Γ A B R ( x , y , z ) d z \begin{aligned} ①& \ \ \int_{\Gamma_{AB}}(\vec{A}\cdot\vec{T^0})ds\\ ②& \ \ =\int_{\Gamma_{AB}}\vec{A}\cdot d\vec{s}\\ ③& \ \ =\int_{\Gamma_{AB}}(P(x,y,z)\cos\alpha+Q(x,y,z)\cos\beta+R(x,y,z)\cos\gamma)ds\\ & \ \ =\int_{\Gamma_{AB}}(P\cos\alpha+Q\cos\beta+R\cos\gamma)ds\\ ④& \ \ =\int_{\Gamma_{AB}}P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz\\ & \ \ =\int_{\Gamma_{AB}}Pdx+Qdy+Rdz\ \ \ (用得较多)\\ ⑤& \ \ =\int_{\Gamma_{AB}}P(x,y,z)dx+\int_{\Gamma_{AB}}Q(x,y,z)dy+\int_{\Gamma_{AB}}R(x,y,z)dz \end{aligned} ①②③④⑤ ∫ΓAB(A⋅T0)ds =∫ΓABA⋅ds =∫ΓAB(P(x,y,z)cosα+Q(x,y,z)cosβ+R(x,y,z)cosγ)ds =∫ΓAB(Pcosα+Qcosβ+Rcosγ)ds =∫ΓABP(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz =∫ΓABPdx+Qdy+Rdz (用得较多) =∫ΓABP(x,y,z)dx+∫ΓABQ(x,y,z)dy+∫ΓABR(x,y,z)dz
三、Calculation of curve integrals of the second kind
01 Plane curve integrals of the second kind
If you directly calculate the two-curve integral,Which one to turn into?
If the second kind of curve integral is calculated directly,No matter which form is given, it must be turned into the first④种,把曲线 Γ A B \Gamma_{AB} ΓAB represented as a parametric equation:
Γ A B : { x = x ( t ) y = y ( t ) \Gamma_{AB}:\ \begin{cases}\ x=x(t) \\ \ y=y(t) \end{cases} ΓAB: { x=x(t) y=y(t) 找出起点 A A A 对应的参数 t A t_A tA,找出终点 B B B 对应的参数 t B t_B tB .
∫ Γ A B P d x + Q d y = ∫ t A t B [ P ( x ( t ) , y ( t ) ) x ′ ( t ) + Q ( x ( t ) , y ( t ) ) y ′ ( t ) ] d t \begin{aligned} & \int_{\Gamma_{AB}}Pdx+Qdy=\int_{t_A}^{t_B}[P(x(t),y(t))x'(t)+Q(x(t),y(t))y'(t)]dt \end{aligned} ∫ΓABPdx+Qdy=∫tAtB[P(x(t),y(t))x′(t)+Q(x(t),y(t))y′(t)]dt
对于平面曲线 Γ A B \Gamma_{AB} ΓAB,in five“Plane curve integrals of the second kind“的基础上,The equation of the curve has the following situations.
(1) Unary function type
形式: Γ A B : y = φ ( x ) , x ∈ [ a , b ] \Gamma_{AB}:y=\varphi(x),x\in[a,b] ΓAB:y=φ(x),x∈[a,b],( x = x x=x x=x ) Special parametric equations
(2) Constant function type
形式: Γ A B : y = a ( 常数 ) \Gamma_{AB}:y=a\ (常数) ΓAB:y=a (常数), ( x = x x=x x=x ) Special parametric equations
(3) Unary inverse function type
形式: Γ A B : x = ψ ( y ) , y ∈ [ c , d ] , ψ ’ ( x ) \Gamma_{AB}:x=\psi(y)\ , \ y\in[c,d]\ , \ \psi’(x) ΓAB:x=ψ(y) , y∈[c,d] , ψ’(x) 连续 ( y = y y=y y=y ) Special parametric equations
(4) Inverse function constant type
形式: Γ A B : x = a ( 常数 ) , y ∈ [ c , d ] , ψ ’ ( x ) \Gamma_{AB}:x=a\ (常数)\ , \ y\in[c,d]\ , \ \psi’(x) ΓAB:x=a (常数) , y∈[c,d] , ψ’(x) 连续 ( y = y y=y y=y ) Special parametric equations
(5) Polar coordinate type
形式: Γ A B : r = r ( θ ) , θ ∈ [ α , β ] , r ′ ( θ ) \Gamma_{AB}:r=r(\theta)\ , \ \theta\in[\alpha,\beta]\ , \ r'(\theta) ΓAB:r=r(θ) , θ∈[α,β] , r′(θ) 连续
⇒ { x = r ( θ ) cos θ y = r ( θ ) sin θ θ ∈ [ α , β ] \Rightarrow\ \begin{cases}\ x=r(\theta)\cos\theta \\ \ y=r(\theta)\sin\theta\end{cases}\quad\theta\in[\alpha,\beta] ⇒ { x=r(θ)cosθ y=r(θ)sinθθ∈[α,β] , x ′ 2 ( θ ) + y ′ 2 ( θ ) = r 2 ( θ ) + r ′ 2 ( θ ) x'^2(\theta)+y'^2(\theta)=r^2(\theta)+r'^2(\theta) x′2(θ)+y′2(θ)=r2(θ)+r′2(θ)
(6) Inverse polar type
形式: Γ A B : θ = θ ( r ) , r ∈ [ a , b ] , θ ′ ( r ) \Gamma_{AB}:\theta=\theta(r)\ , \ r\in[a,b]\ , \ \theta'(r) ΓAB:θ=θ(r) , r∈[a,b] , θ′(r) 连续
⇒ { x = r cos θ ( r ) y = r sin θ ( r ) r ∈ [ a , b ] \Rightarrow\ \begin{cases}\ x=r\cos\theta(r) \\ \ y=r\sin\theta(r)\end{cases}\quad r\in[a,b] ⇒ { x=rcosθ(r) y=rsinθ(r)r∈[a,b]
02 Curve integrals of the second kind in space
(1) Closed curve type
形式: ∮ L P d x + Q d y + R d z \oint_{L}Pdx+Qdy+Rdz ∮LPdx+Qdy+Rdz
① 直接计算
Calculate directly if you can, L : { x = x ( t ) y = y ( t ) z = z ( t ) L:\ \begin{cases}\ x=x(t) \\ \ y=y(t) \\ \ z=z(t)\end{cases} L: ⎩⎨⎧ x=x(t) y=y(t) z=z(t) ,Find the parameter corresponding to the starting point t 0 t_0 t0,Find the parameter corresponding to the end point t 1 t_1 t1 .into a definite integral of the parameters.
② 斯托克斯公式
(2) Unclosed curve type
形式: ∫ Γ A B P d x + Q d y + R d z \int_{\Gamma_{AB}}Pdx+Qdy+Rdz ∫ΓABPdx+Qdy+Rdz
① 直接计算
Calculate directly if you can, Γ A B : { x = x ( t ) y = y ( t ) z = z ( t ) \Gamma_{AB}:\ \begin{cases}\ x=x(t) \\ \ y=y(t) \\ \ z=z(t)\end{cases} ΓAB: ⎩⎨⎧ x=x(t) y=y(t) z=z(t) 找出起点 A A A 对应的参数 t A t_A tA,找出终点 B B B 对应的参数 t B t_B tB .into a definite integral of the parameters.
② 牛顿-莱布尼兹公式
若找到 u ( x , y , z ) u(x,y,z) u(x,y,z),使 d u = P d x + Q d y + R d z du=Pdx+Qdy+Rdz du=Pdx+Qdy+Rdz,
∫ Γ A B P d x + Q d y + R d z = ∫ A ( x 0 , y 0 , z 0 ) B ( x 1 , y 1 , z 1 ) d u = u ( x , y , z ) ∣ A ( x 0 , y 0 , z 0 ) B ( x 1 , y 1 , z 1 ) \displaystyle{ \int_{\Gamma_{AB}}Pdx+Qdy+Rdz=\int_{A(x_0,y_0,z_0)}^{B(x_1,y_1,z_1)}du=u(x,y,z)\Big|_{A(x_0,y_0,z_0)}^{B(x_1,y_1,z_1)} } ∫ΓABPdx+Qdy+Rdz=∫A(x0,y0,z0)B(x1,y1,z1)du=u(x,y,z)∣∣A(x0,y0,z0)B(x1,y1,z1)
∫ A ( x 0 , y 0 , z 0 ) B ( x 1 , y 1 , z 1 ) P d x + Q d y + R d z = ∫ x 0 x 1 P ( x , y 0 , z 0 ) d x + ∫ y 0 y 1 Q ( x 1 , y , z 0 ) d y + ∫ z 0 z 1 R ( x 1 , y 1 , z ) d z \displaystyle{ \int_{A(x_0,y_0,z_0)}^{B(x_1,y_1,z_1)}Pdx+Qdy+Rdz=\int_{x_0}^{x_1}P(x,y_0,z_0)dx+\int_{y_0}^{y_1}Q(x_1,y,z_0)dy+\int_{z_0}^{z_1}R(x_1,y_1,z)dz }% ∫A(x0,y0,z0)B(x1,y1,z1)Pdx+Qdy+Rdz=∫x0x1P(x,y0,z0)dx+∫y0y1Q(x1,y,z0)dy+∫z0z1R(x1,y1,z)dz
③ 路径无关
Find the line simply connected Ω \Omega Ω 使 Γ A B ⊂ Ω \Gamma_{AB}\subset\Omega ΓAB⊂Ω,有 P , Q , R P\ , \ Q\ , \ R P , Q , R 偏导数连续,且 r o t A ⃗ ≡ 0 \mathrm{rot}\vec{A}\equiv0 rotA≡0,Knowing has nothing to do with paths.
∫ A ( x 0 , y 0 , z 0 ) B ( x 1 , y 1 , z 1 ) P ( x , y , z ) d x + Q ( x , y , z ) d y + R ( x , y , z ) d z \displaystyle{ \int_{A(x_0,y_0,z_0)}^{B(x_1,y_1,z_1)}P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz }% ∫A(x0,y0,z0)B(x1,y1,z1)P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz
= ∫ x 0 x 1 P ( x , y 0 , z 0 ) d x + ∫ y 0 y 1 Q ( x 1 , y , z 0 ) d y + ∫ z 0 z 1 R ( x 1 , y 1 , z ) d z \displaystyle{ =\int_{x_0}^{x_1}P(x,y_0,z_0)dx+\int_{y_0}^{y_1}Q(x_1,y,z_0)dy+\int_{z_0}^{z_1}R(x_1,y_1,z)dz }% =∫x0x1P(x,y0,z0)dx+∫y0y1Q(x1,y,z0)dy+∫z0z1R(x1,y1,z)dz
将 x 1 x_1 x1 换成 x x x,同理有:
u ( x , y , z ) = ∫ A ( x 0 , y 0 , z 0 ) B ( x 1 , y 1 , z 1 ) P d x + Q d y + R d z + C \displaystyle{ u(x,y,z)=\int_{A(x_0,y_0,z_0)}^{B(x_1,y_1,z_1)}Pdx+Qdy+Rdz+C }% u(x,y,z)=∫A(x0,y0,z0)B(x1,y1,z1)Pdx+Qdy+Rdz+C (与路径无关)
= ∫ x 0 x P ( x , y 0 , z 0 ) d x + ∫ y 0 y Q ( x , y , z 0 ) d y + ∫ z 0 z R ( x , y , z ) d z + C \displaystyle{ =\int_{x_0}^{x}P(x,y_0,z_0)dx+\int_{y_0}^{y}Q(x,y,z_0)dy+\int_{z_0}^{z}R(x,y,z)dz+C }% =∫x0xP(x,y0,z0)dx+∫y0yQ(x,y,z0)dy+∫z0zR(x,y,z)dz+C
四、Eight types of problem solving for curve integral of the second kind of plane
Four equivalent conditions for path-independent integration of plane curves using Green's formula,Discuss the following types.
01 Closed curve type
形式: ∮ Γ P ( x , y ) d x + Q ( x , y ) d y \oint_{\Gamma}P(x,y)dx+Q(x,y)dy ∮ΓP(x,y)dx+Q(x,y)dy, Γ \Gamma Γ is a closed curve,along the positive direction.
首先需要求出 ∂ Q ∂ x , ∂ P ∂ y \displaystyle{\frac{\partial Q}{\partial x} \ , \ \frac{\partial P}{\partial y} }% ∂x∂Q , ∂y∂P ,Then there are the following discussions of three different situations:
① 若 P P P, Q Q Q 在 Γ \Gamma Γ 包围的区域 D D D is continuous and has continuous first-order partial derivatives,Use Green's formula:
∮ Γ P ( x , y ) d x + Q ( x , y ) d y = ∬ D ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y \displaystyle{\oint_{\Gamma}P(x,y)dx+Q(x,y)dy=\iint\limits_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y} ∮ΓP(x,y)dx+Q(x,y)dy=D∬(∂x∂Q−∂y∂P)dxdy ( The double integral is required to be easily calculated )
② 在 Γ \Gamma Γ 包围的区域 D D D 内部有”洞“(所谓”洞“,主要指的是 P P P, Q Q Q Not defined in this area)
在”洞“的外部, P P P, Q Q Q The partial derivatives of are continuous and have ∂ Q ∂ x ≡ ∂ P ∂ y \displaystyle{\frac{\partial Q}{\partial x}\equiv\frac{\partial P}{\partial y} }% ∂x∂Q≡∂y∂P ,
则 ∮ Γ + P d x + Q d y = ∮ Γ 1 + P d x + Q d y , Γ , Γ 1 \oint_{\Gamma^+}Pdx+Qdy=\oint_{\Gamma_1^+}Pdx+Qdy\ ,\ \Gamma,\Gamma_1 ∮Γ+Pdx+Qdy=∮Γ1+Pdx+Qdy , Γ,Γ1 surround the same”洞“,同方向.
Justify the conclusion:
证明 : ∮ Γ + + Γ 1 − P d x + Q d y = ∬ D 1 ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y = ∬ D 1 0 d x d y = 0 ∮ Γ + P d x + Q d y + ∮ Γ 1 − P d x + Q d y = 0 ∮ Γ + P d x + Q d y − ∮ Γ 1 + P d x + Q d y = 0 ∮ Γ + P d x + Q d y = ∮ Γ 1 + P d x + Q d y \begin{aligned} & 证明:\oint_{\Gamma^++\Gamma_1^-}Pdx+Qdy=\iint\limits_{D_1}(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy=\iint\limits_{D_1}0dxdy=0\\ & \quad\quad\ \oint_{\Gamma^+}Pdx+Qdy+\oint_{\Gamma_1^-}Pdx+Qdy=0\\ & \quad\quad\ \oint_{\Gamma^+}Pdx+Qdy-\oint_{\Gamma_1^+}Pdx+Qdy=0\\ & \quad\quad\ \oint_{\Gamma^+}Pdx+Qdy=\oint_{\Gamma_1^+}Pdx+Qdy\\ \end{aligned} 证明:∮Γ++Γ1−Pdx+Qdy=D1∬(∂x∂Q−∂y∂P)dxdy=D1∬0dxdy=0 ∮Γ+Pdx+Qdy+∮Γ1−Pdx+Qdy=0 ∮Γ+Pdx+Qdy−∮Γ1+Pdx+Qdy=0 ∮Γ+Pdx+Qdy=∮Γ1+Pdx+Qdy
常用场景:
P , Q 分母为 a x 2 + b y 2 ( a > 0 , b > 0 , 常数 ) 如 Γ Surrounds the origin O ( 0 , 0 ) ,此时 0 为洞. 若不在 O 点时, P , Q Partial derivatives are continuous and ∂ Q ∂ x ≡ ∂ P ∂ y 选取 Γ 1 : a x 2 + b y 2 = R 2 ( R > 0 ,常数 ) 经常 R = 1 , Γ 1 与 Γ 同方向 化成 Γ 1 Curve integrals of the second kind on . The denominator at this time a x 2 + b y 2 = R 2 ,化简后的 P , Q Expressions made simple ( 科学瘦身 ) 此时,偏导数连续,Green's formula can be used. \begin{aligned} & P\ ,\ Q\ 分母为\ ax^2+by^2 \ (a>0,b>0,常数)\\ & 如\ \Gamma Surrounds the origin\ O(0,0),此时\ 0 \ 为洞.\\ & 若不在O点时,\\ & P\ ,\ QPartial derivatives are continuous and \ \frac{\partial Q}{\partial x}\equiv\frac{\partial P}{\partial y}\\ & 选取\Gamma_1:ax^2+by^2=R^2\ (R>0,常数)\\ & 经常R=1,\Gamma_1与\Gamma同方向\\ & 化成\Gamma_1Curve integrals of the second kind on .\\ & The denominator at this timeax^2+by^2=R^2,化简后的P\ ,\ QExpressions made simple\ (科学瘦身)\\ & 此时,偏导数连续,Green's formula can be used. \end{aligned} P , Q 分母为 ax2+by2 (a>0,b>0,常数)如 ΓSurrounds the origin O(0,0),此时 0 为洞.若不在O点时,P , QPartial derivatives are continuous and ∂x∂Q≡∂y∂P选取Γ1:ax2+by2=R2 (R>0,常数)经常R=1,Γ1与Γ同方向化成Γ1Curve integrals of the second kind on .The denominator at this timeax2+by2=R2,化简后的P , QExpressions made simple (科学瘦身)此时,偏导数连续,Green's formula can be used.
③ 如果 Γ \Gamma Γ The definite integral expressed as a parametric equation simplifies into a one-variable function is easy to integrate,也可以直接计算.
02 Unclosed curve type
形式: ∫ Γ A B P ( x , y ) d x + Q ( x , y ) d y \int_{\Gamma_{AB}}P(x,y)dx+Q(x,y)dy ∫ΓABP(x,y)dx+Q(x,y)dy, Γ A B \Gamma_{AB} ΓAB is a non-closed curve in the plane.
首先需要求出 ∂ Q ∂ x , ∂ P ∂ y \displaystyle{\frac{\partial Q}{\partial x} \ , \ \frac{\partial P}{\partial y} }% ∂x∂Q , ∂y∂P ,Then there are the following discussions of three different situations:
① 如果 ( x , y ) ∈ Γ A B (x,y)\in\Gamma_{AB} (x,y)∈ΓAB, ∂ Q ∂ x = ∂ P ∂ y \displaystyle{\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y} }% ∂x∂Q=∂y∂P 连续,in the area shown in the figure D D D 上, ∂ Q ∂ x = ∂ P ∂ y \displaystyle{\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y} }% ∂x∂Q=∂y∂P 连续,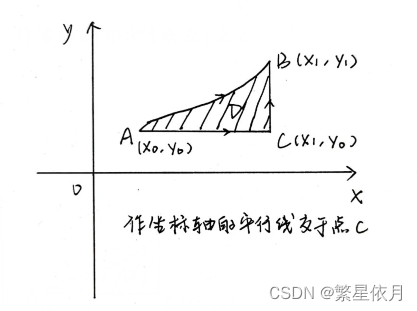
A C → : y = y 0 ( x = x ) Special parametric equations { A : x 0 C : x 1 \overrightarrow{AC}:\ y=y_0\ (x=x)\ Special parametric equations \begin{cases}\ A:x_0 \\ \ C:x_1 \end{cases} AC: y=y0 (x=x) Special parametric equations{ A:x0 C:x1 ,
C B → : x = x 1 ( y = y ) Special parametric equations { C : y 0 B : y 1 \overrightarrow{CB}:\ x=x_1\ (y=y)\ Special parametric equations \begin{cases}\ C:y_0 \\ \ B:y_1 \end{cases} CB: x=x1 (y=y) Special parametric equations{ C:y0 B:y1 .
∫ Γ A B P ( x , y ) d x + Q ( x , y ) d y = ∫ A ( x 0 , y 0 ) B ( x 1 , y 1 ) P d x + Q d y = ∫ A C → P ( x , y ) d x + Q ( x , y ) d y + ∫ C B → P ( x , y ) d x + Q ( x , y ) d y = ∫ x 0 x 1 P ( x , y 0 ) d x + ∫ y 0 y 1 Q ( x 1 , y ) d y \begin{aligned} & \int_{\Gamma_{AB}}P(x,y)dx+Q(x,y)dy=\int_{A(x_0,y_0)}^{B(x_1,y_1)}Pdx+Qdy \\ & =\int_{\overrightarrow{AC}}P(x,y)dx+Q(x,y)dy+ \int_{\overrightarrow{CB}}P(x,y)dx+Q(x,y)dy\\ & =\int_{x_0}^{x_1}P(x,y_0)dx+\int_{y_0}^{y_1}Q(x_1,y)dy \end{aligned} ∫ΓABP(x,y)dx+Q(x,y)dy=∫A(x0,y0)B(x1,y1)Pdx+Qdy=∫ACP(x,y)dx+Q(x,y)dy+∫CBP(x,y)dx+Q(x,y)dy=∫x0x1P(x,y0)dx+∫y0y1Q(x1,y)dy
② 若 ( x , y ) ∈ Γ A B (x,y)\in\Gamma_{AB} (x,y)∈ΓAB, ∂ Q ∂ x ≢ ∂ P ∂ y \displaystyle{\frac{\partial Q}{\partial x}\not\equiv\frac{\partial P}{\partial y} }% ∂x∂Q≡∂y∂P ,
∫ Γ A B P d x + Q d y = ∫ Γ A B + l P d x + Q d y − ∫ l P d x + Q d y \displaystyle{ \int_{\Gamma_{AB}}Pdx+Qdy=\int_{\Gamma_{AB}+l}Pdx+Qdy-\int_{l}Pdx+Qdy }% ∫ΓABPdx+Qdy=∫ΓAB+lPdx+Qdy−∫lPdx+Qdy
其中 l l l A simple curve is required,Often a directed straight line segment,The former uses Green's formula,The latter is calculated directly.
③ 如果 Γ A B \Gamma_{AB} ΓAB can be expressed as a parametric equation,Definite integrals of unary functions that are transformed into parameters,容易计算,也可以直接计算.
03 求原函数
形式:求 P ( x , y ) d x + Q ( x , y ) d y P(x,y)dx+Q(x,y)dy P(x,y)dx+Q(x,y)dy 的原函数
Recall the unary primitive function:若 F ′ ( x ) = f ( x ) F'(x)=f(x) F′(x)=f(x),称 F ( x ) F(x) F(x) 是 f ( x ) f(x) f(x) 在区间 I I I 上的一个原函数.
Speaking of primitive functions of two variables:Must be the original function of a pair of functions,满足 u = u ( x , y ) , ∂ u ∂ x = P ( x , y ) , ∂ u ∂ y = Q ( x , y ) \displaystyle{u=u(x,y)\ , \ \frac{\partial u}{\partial x}=P(x,y)\ , \ \frac{\partial u}{\partial y}=Q(x,y) }% u=u(x,y) , ∂x∂u=P(x,y) , ∂y∂u=Q(x,y) ,
即满足 d F ( x ) = f ( x ) d x ⇒ d u = P d x + Q d y dF(x)=f(x)dx\ \Rightarrow\ du=Pdx+Qdy dF(x)=f(x)dx ⇒ du=Pdx+Qdy .
什么条件下 P , Q P\ , \ Q P , Q 有原函数?
Find a simply connected region D D D, P , Q P\ , \ Q P , Q 在 D D D The upper partial derivative is continuous,且 ∂ Q ∂ x = ∂ P ∂ y , ( x , y ) ∈ D \displaystyle{\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}\ , \ (x,y)\in D }% ∂x∂Q=∂y∂P , (x,y)∈D .
By path independent line,know③Article established,存在 D D D a binary function on ,使得:
u ( x , y ) = ∫ A ( x 0 , y 0 ) B ( x 1 , y 1 ) P ( x , y ) d x + Q ( x , y ) d y + C = ∫ x 0 x P ( x , y 0 ) d x + ∫ y 0 y Q ( x , y ) d y + C 使得, d u = P d x + Q d y ,即 ∂ u ∂ x = P , ∂ u ∂ y = Q \begin{aligned} & u(x,y)=\int_{A(x_0,y_0)}^{B(x_1,y_1)}P(x,y)dx+Q(x,y)dy+C \\ & =\int_{x_0}^{x}P(x,y_0)dx+\int_{y_0}^{y}Q(x,y)dy+C\\ & 使得,du=Pdx+Qdy,即\ \frac{\partial u}{\partial x}=P\ , \ \frac{\partial u}{\partial y}=Q\\ \end{aligned} u(x,y)=∫A(x0,y0)B(x1,y1)P(x,y)dx+Q(x,y)dy+C=∫x0xP(x,y0)dx+∫y0yQ(x,y)dy+C使得,du=Pdx+Qdy,即 ∂x∂u=P , ∂y∂u=Q
称 u ( x , y ) u(x,y) u(x,y) 是 P ( x , y ) d x + Q ( x , y ) d y P(x,y)dx+Q(x,y)dy P(x,y)dx+Q(x,y)dy 的 (全体) 原函数.
04 Solve full differential equations
形如 P ( x , y ) d x + Q ( x , y ) d y = 0 P(x,y)dx+Q(x,y)dy=0 P(x,y)dx+Q(x,y)dy=0,If there is a simply connected region D D D,使 ∂ Q ∂ x ≡ ∂ P ∂ y \displaystyle{\frac{\partial Q}{\partial x}\equiv\frac{\partial P}{\partial y} }% ∂x∂Q≡∂y∂P 连续,In this case this equation is called a total differential equation.
由 (3) 知, u ( x , y ) = ∫ x 0 x P ( x , y 0 ) d x + ∫ y 0 y Q ( x , y ) d y u(x,y)=\int_{x_0}^{x}P(x,y_0)dx+\int_{y_0}^{y}Q(x,y)dy u(x,y)=∫x0xP(x,y0)dx+∫y0yQ(x,y)dy,
由 P d x + Q d y = 0 Pdx+Qdy=0 Pdx+Qdy=0, ⇔ d u ( x , y ) = 0 \Leftrightarrow\ du(x,y)=0 ⇔ du(x,y)=0 ⇔ u ( x , y ) = C ( C 常, C ∈ R ) \Leftrightarrow\ u(x,y)=C\ (C常,C\in R) ⇔ u(x,y)=C (C常,C∈R)
⇔ ∫ x 0 x P ( x , y 0 ) d x + ∫ y 0 y Q ( x , y ) d y = C \Leftrightarrow\ \int_{x_0}^{x}P(x,y_0)dx+\int_{y_0}^{y}Q(x,y)dy=C ⇔ ∫x0xP(x,y0)dx+∫y0yQ(x,y)dy=C 是方程的通解.
Total differential quadrature(全微分方程)
设函数 P ( x , y ) , Q ( x , y ) P(x, y), Q(x, y) P(x,y),Q(x,y) on a simply connected region D D D 有连续导数,且
∂ Q ∂ x = ∂ P ∂ y \frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y} ∂x∂Q=∂y∂P
则 P d x + Q d y P d x+Q d y Pdx+Qdy 是某个函数 u u u 的全微分:
u ( x , y ) = ∫ ( x 0 , y 0 ) ( x , y ) P d x + Q d y ← ( u 的求法 ) u(x, y)=\int_{\left(x_{0}, y_{0}\right)}^{(x, y)} P d x+Q d y\quad\leftarrow(u的求法) u(x,y)=∫(x0,y0)(x,y)Pdx+Qdy←(u的求法)
若 P ( x , y ) d x + Q ( x , y ) d y P(x, y) d x+Q(x, y) d y P(x,y)dx+Q(x,y)dy is the total differential of a function of two variables,称方程 P d x + Q d y = 0 P d x+Q d y=0 Pdx+Qdy=0 为全微分方程.
求出原函数 u u u,则解为 u = C u=C u=C .
若 P ( x , y ) d x + Q ( x , y ) d y P(x, y) \mathrm{dx}+Q(x, y) \mathrm{d} \mathrm{y} P(x,y)dx+Q(x,y)dy is not the total differential of a binary function,方程 P d x + Q d y = 0 P d x+Q d y=0 Pdx+Qdy=0 的解法:
Find the integral factor μ \mu μ,so that the equation becomes μ P ( x , y ) d x + μ Q ( x , y ) d y = 0 \mu P(x, y) d x+\mu Q(x, y) d y=0 μP(x,y)dx+μQ(x,y)dy=0 becomes a total differential equation.
Common integral factors : 1 x 2 , 1 y 2 , 1 x y , 1 x 2 y 2 , 1 x 2 + y 2 Combination patchwork : 例如,求解方程① ( x − x 2 + y 2 ) d x = − y d y ( Grouping and combining make up the full differential,Observe what factors need to be multiplied during the process ) ( x d x + y d y ) − x 2 + y 2 d x = 0 ⇒ d ( x 2 + y 2 ) − x 2 + y 2 d x = 0 Multiply by what makes the latter term fully differentiated , The former term is still total differential ? 若将 x 2 + y 2 看作 u , should be multiplied by φ ( u ) In fact, as long as each group makes up the full differential,The equation is solved 求解方程② y ( 1 + x y ) d x + x ( 1 − x y ) d y = 0 \begin{aligned} & Common integral factors:\ \frac{1}{x^{2}}, \frac{1}{y^{2}}, \frac{1}{x y}, \frac{1}{x^{2} y^{2}}, \frac{1}{x^{2}+y^{2}}\\ & Combination patchwork:\ \\ & 例如,求解方程①\ \left(x-\sqrt{x^{2}+y^{2}}\right) d x=-y d y\ \ (Grouping and combining make up the full differential,Observe what factors need to be multiplied during the process)\\ &\quad\quad\quad\quad\quad(x d x+y d y)-\sqrt{x^{2}+y^{2}} d x=0 \Rightarrow d\left(x^{2}+y^{2}\right)-\sqrt{x^{2}+y^{2}} d x=0 \\ & \quad\quad\quad\quad\quadMultiply by what makes the latter term fully differentiated,The former term is still total differential?\ 若将 x^{2}+y^{2} 看作 u, should be multiplied by \varphi(u)\\ & \quad\quad\quad\quad\quadIn fact, as long as each group makes up the full differential,The equation is solved\\ & 求解方程②\ \ y(1+x y) d x+x(1-x y) d y=0 \end{aligned} Common integral factors: x21,y21,xy1,x2y21,x2+y21Combination patchwork: 例如,求解方程① (x−x2+y2)dx=−ydy (Grouping and combining make up the full differential,Observe what factors need to be multiplied during the process)(xdx+ydy)−x2+y2dx=0⇒d(x2+y2)−x2+y2dx=0Multiply by what makes the latter term fully differentiated,The former term is still total differential? 若将x2+y2看作u,should be multiplied byφ(u)In fact, as long as each group makes up the full differential,The equation is solved求解方程② y(1+xy)dx+x(1−xy)dy=0
05 Points include reference questions
形式: P ( x , y ) d x + Q ( x , y ) d y P(x,y)dx+Q(x,y)dy P(x,y)dx+Q(x,y)dy 中,求 P , Q P\ , \ Q P , Q Alphabetical constants in .
P ( x , y ) d x + Q ( x , y ) d y P(x,y)dx+Q(x,y)dy P(x,y)dx+Q(x,y)dy 中, P , Q P\ , \ Q P , Q The expression contains the letter constant to be evaluated,Find this letter constant.
Find a simply connected region D D D, P , Q P\ , \ Q P , Q 在 D D D The upper partial derivative is continuous,根据题目条件,验证 ① ∼ \sim ∼③One of the articles is established,
从而第④Article established,即有 ∂ Q ∂ x ≡ ∂ P ∂ y \displaystyle{\frac{\partial Q}{\partial x}\equiv\frac{\partial P}{\partial y} }% ∂x∂Q≡∂y∂P ,Find the value of the letter constant from it.
06 牛顿-莱布尼兹公式
若 P , Q P\ ,\ Q P , Q 在单连通区域 D D D 上连续, Γ A B ⊂ D \Gamma_{AB}\subset D ΓAB⊂D,且存在 D D D 上的二元函数 u ( x , y ) u(x,y) u(x,y),使 d u = P d x + Q d y du=Pdx+Qdy du=Pdx+Qdy,
∫ Γ A B P d x + Q d y = ∫ A B d u = u ( x , y ) ∣ A ( x 0 , y 0 ) B ( x 1 , y 1 ) = u ( x 1 , y 1 ) − u ( x 0 , y 0 ) \int_{\Gamma_{AB}}Pdx+Qdy=\int_{AB}du=u(x,y)\Big|_{A(x_0,y_0)} ^{B(x_1,y_1)}=u(x_1,y_1)-u(x_0,y_0) ∫ΓABPdx+Qdy=∫ABdu=u(x,y)∣∣A(x0,y0)B(x1,y1)=u(x1,y1)−u(x0,y0)
07 求面积
There is a closed area D D D 的边界为 Γ \Gamma Γ along the positive direction, D D D 的面积为 S S S,则 S = ∫ D 1 d σ = 1 2 ∮ Γ + − y d x + x d y S=\int_D1d\sigma=\frac12\oint_{\Gamma^+}-ydx+xdy S=∫D1dσ=21∮Γ+−ydx+xdy Calculate directly on the right.
08 物理应用
Find a point M M M 在变力 F ⃗ \vec{F} F Acts along the curve Γ A B \Gamma_{AB} ΓAB 由 A A A 移动到 B B B 所作的功 W W W, W = ∫ Γ A B ( F ⃗ ⋅ T 0 ⃗ ) d s W=\int_{\Gamma_{AB}}(\vec{F}\cdot\vec{T^0})ds W=∫ΓAB(F⋅T0)ds .
边栏推荐
- 桌面软件开发框架大赏
- Field interpretation under "Surgical variables (RX SUMM-SURG OTH REG/DIS)" in SEER database
- 网络/信息安全顶刊及相关期刊会议
- 经典毕业设计:基于SSM实现高校后勤报修系统
- [Mini Program Column] Summarize the development specifications of uniapp to develop small programs
- 一文带你玩转offer-01
- 一文读懂二十种开关电源拓扑结构
- 电源完整性的去耦和层间耦合电容
- 基于JSP实现校园二手交易平台
- 2022杭电多校第一场
猜你喜欢
![[Yugong Series] July 2022 Go Teaching Course 021-Slicing Operation of Go Containers](/img/ff/f3de4952d64afe36c515a2220bfe9d.png)
[Yugong Series] July 2022 Go Teaching Course 021-Slicing Operation of Go Containers

20个电路能懂5个以上,足以证明你在电子行业混过!
【网络攻防】常见的网络攻防技术——黑客攻防(通俗易懂版)
【HMS core】【FAQ】HMS Toolkit典型问题合集1

嘉为鲸翼·多云管理平台荣获信通院可信云技术服务最佳实践

PCB板加工流程中哪些因素会影响到传输线阻抗
![[Mini Program Column] Summarize the development specifications of uniapp to develop small programs](/img/7b/110d324eba00652e4987bc623a5bc6.png)
[Mini Program Column] Summarize the development specifications of uniapp to develop small programs

Circuit analysis: constant current source circuit composed of op amp and triode

函数(1)

hicp第六天
随机推荐
积分专题笔记-曲线面积分三大公式
The FPGA based protocol 2: the I2C read and write E squared PROM
typescript7-typescript常用类型
编程界的“躲猫猫”比赛 | 每日趣闻
typescript6 - simplify the steps to run ts
EMC过不了?都是PCB工程师的锅?
剑指offer 48:最长不重复子串
Golang DES 加解密如何实现?
ACL 2022 | 引入角度margin构建对比学习目标,增强文本语义判别能力
ant-design form表单校验upload组件(附个人封装的上传组件)
Why does typescript2-typescript add type support to js
Judging from the Internet:
回板后,处理器不启动,怎么办?
积分简明笔记-第二类曲线积分的类型
function (1)
js currying
[Fun BLDC series with zero basics] Taking GD32F30x as an example, the timer related functions are explained in detail
涛思 TDengine 2.6+优化参数
hicp第六天
OA Project Pending Meeting & History Meeting & All Meetings