特征降维学习笔记（pca和lda）（1）

现在存在两种主流的降维方式：投影与流形学习，投影是指将高维数据投影在低维度的平面上，但是可能导致子空间旋转扭曲。而流形学习依赖于流形设计，流形设计主要认为现实世界高维数据集接近于低维度流体。

主成分分析（PCA）：它是通过识别靠近数据的超平面进行投影，本质上是通过比较原始数据集，到新平面的方差最小，则为第一主成分，当第二个主成分与第一个组成分的协方差为0，说明不相关，则为第二个主成分，以此类推。

使用python计算pca：

import  numpy as np
np.random.seed(4)
m = 60
w1, w2 = 0.1, 0.3
noise = 0.1

angles = np.random.rand(m) * 3 * np.pi / 2 - 0.5
X = np.empty((m, 3))
X[:, 0] = np.cos(angles) + np.sin(angles)/2 + noise * np.random.randn(m) / 2
X[:, 1] = np.sin(angles) * 0.7 + noise * np.random.randn(m) / 2
X[:, 2] = X[:, 0] * w1 + X[:, 1] * w2 + noise * np.random.randn(m)
X_centered = X-X.mean(axis=0)
U,S,Vt =np.linalg.svd(X_centered)
c1 = Vt.T[:,0]
c2 = Vt.T[:,1]
w2 =Vt.T[:,:2]
X2D = X_centered.dot(w2)
X2D

这里使用了svd方法（奇异值分解），它的作用是旋转坐标轴，进行拉伸后再进行旋转，计算均值的目的是在计算主成分的过程中，需要得到每一类主成分的均值，进而使每一类主成分的均值点距离最大，而每一类样本点中间的差异最小。

使用sklearn中的decomposition的pca方法进行模拟

from sklearn.decomposition import PCA
pca =PCA(n_components=2)
X_2D =pca.fit_transform(X)
pca.components_.T[:,0]##第一个主成分的单位向量

在主成分分析中，有一类方法，累计求主成分的和，当总的主成分大于95%时，就取这些主成分作为全部分成进行计算。

pca.explained_variance_ratio_##可解释方差比，说明前两个主成分的方差占比

这里使用pca的函数explained_variance_ratio可解释方差，本质是就是特征的重要性。

from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1, as_frame=False)
mnist.target = mnist.target.astype(np.uint8)
from sklearn.model_selection import train_test_split
X = mnist["data"]
y = mnist["target"]
X_train, X_test, y_train, y_test = train_test_split(X, y)
pca = PCA()
pca.fit_transform(X_train)
cumsum = np.cumsum(pca.explained_variance_ratio_)##对数据按行求和
d = np.argmax(cumsum>0.95)+1

也可以通过pca的超参数进行设置

pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X_train)

也可以在pca中设置参数，对数据进行压缩

##使用pca进行压缩
pca = PCA(n_components=154)
x_reduced = pca.fit_transform(X_train)
x_reversed = pca.inverse_transform(x_reduced)

pca.inverse_transform可以将压缩特征进行还原。

随机pca：快速找到前d个主成分的近似值。pca中的svd_solver='randomized'

rnd_pca = PCA(n_components=154,svd_solver = 'randomized')
x_reduced = rnd_pca.fit_transform(X_train)
rnd_pca.explained_variance_ratio_.sum()

增量pca：将小批量的数据送入内存进行降维，完成后再输入少量数据，增加运行速度，同时节约了内存空间。这里使用了sklearn.decomposition.incrementalPCA

from sklearn.decomposition import IncrementalPCA
IPCA  =IncrementalPCA(n_components=154)
n_batches=100
for x_batch in np.array_split(X_train,n_batches):
    IPCA.partial_fit(x_batch)
x_reduced  =IPCA.transform(X_train)

 也可以使用np.menmap类进行操作。

filename = "my_mnist.data"
m, n = X_train.shape

X_mm = np.memmap(filename, dtype='float32', mode='write', shape=(m, n))
X_mm[:] = X_train
X_mm = np.memmap(filename, dtype="float32", mode="readonly", shape=(m, n))

batch_size = m // n_batches
inc_pca = IncrementalPCA(n_components=154, batch_size=batch_size)
inc_pca.fit(X_mm)

内核pca：可以解决非线性的复杂投影，可以使用网格化搜索GridSearchCV进行筛选。

from sklearn.decomposition import KernelPCA
from sklearn.datasets import make_swiss_roll
X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
rbf_pca = KernelPCA(n_components=2,kernel='rbf',gamma=0.04)
x_reduced = rbf_pca.fit_transform(X)
from sklearn.decomposition import KernelPCA
import matplotlib.pyplot as plt

lin_pca = KernelPCA(n_components = 2, kernel="linear", fit_inverse_transform=True)
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.0433, fit_inverse_transform=True)
sig_pca = KernelPCA(n_components = 2, kernel="sigmoid", gamma=0.001, coef0=1, fit_inverse_transform=True)

y = t > 6.9

plt.figure(figsize=(11, 4))
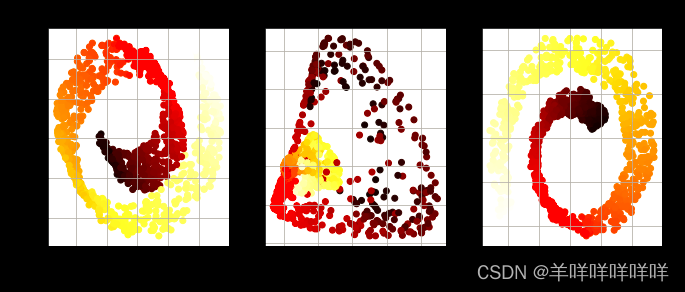
for subplot, pca, title in ((131, lin_pca, "Linear kernel"), (132, rbf_pca, "RBF kernel, $\gamma=0.04$"), (133, sig_pca, "Sigmoid kernel, $\gamma=10^{-3}, r=1$")):
    X_reduced = pca.fit_transform(X)
    if subplot == 132:
        X_reduced_rbf = X_reduced
    
    plt.subplot(subplot)
    #plt.plot(X_reduced[y, 0], X_reduced[y, 1], "gs")
    #plt.plot(X_reduced[~y, 0], X_reduced[~y, 1], "y^")
    plt.title(title, fontsize=14)
    plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot)
    plt.xlabel("$z_1$", fontsize=18)
    if subplot == 131:
        plt.ylabel("$z_2$", fontsize=18, rotation=0)
    plt.grid(True)


plt.show()

from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline

clf = Pipeline([
        ("kpca", KernelPCA(n_components=2)),
        ("log_reg", LogisticRegression(solver="lbfgs"))
    ])

param_grid = [{
        "kpca__gamma": np.linspace(0.03, 0.05, 10),
        "kpca__kernel": ["rbf", "sigmoid"]
    }]

grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X, y)
print(grid_search.best_params_)
rbf_pca = KernelPCA(n_components=2,kernel='rbf',gamma=0.0433,fit_inverse_transform=True)
x_reduced = rbf_pca.fit_transform(X)
X_preimage =rbf_pca.inverse_transform(X_reduced)
from sklearn.metrics import mean_squared_error
mean_squared_error(X,X_preimage)

 习题：使用MNIST数据集训练随机森林分类器，测试其花的时间与性能，然后进行降维后，判断其花费时间与性能，进行比较。

from sklearn.datasets import fetch_openml

mnist = fetch_openml('mnist_784', version=1, as_frame=False)
mnist.target = mnist.target.astype(np.uint8)
X = mnist['data']
Y = mnist['target']
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test =train_test_split(X,Y,test_size=10000)
from sklearn.ensemble import RandomForestClassifier
import time
rfc = RandomForestClassifier()
start_time =time.time()
rfc.fit(x_train,y_train)
end_time = time.time()
print(end_time-start_time)
from sklearn.decomposition import PCA
PCA = PCA(n_components=0.95)
x_reduced_train = PCA.fit_transform(x_train)
rfc_pca = RandomForestClassifier()
start_time =time.time()
rfc_pca.fit(x_reduced_train,y_train)
end_time = time.time()
print(end_time-start_time)
from sklearn.metrics import mean_squared_error
from sklearn.metrics import accuracy_score
def model_descirbe(model,x_test):
    y_pred = model.predict(x_test)
    print('mse',mean_squared_error(y_pred,y_test))
    print('accuracy',accuracy_score(y_pred,y_test))
model_descirbe(rfc)
x_reduced_test = PCA.transform(x_test)
model_descirbe(rfc_pca,x_reduced_test)

结果发现：降维后训练时间边长，而且均方误差与正确率都低于没有降维的