当前位置：网站首页>堆(优先队列)

堆(优先队列)

2022-06-09 20:45:00 【馋学习的身子】

目录

堆的概念

优先队列（Priority Queue）：特殊的“队列”，取出元素的顺序是依照元素的优先权（关键字）大小，而不是元素进入队列的先后顺序。

如何组织优先队列

可以通过数组或者链表实现优先队列：
在这里插入图片描述
那是否有更好的方式实现优先队列呢？

基于完全二叉树的优先队列

在这里插入图片描述
关于完全二叉树的性质：
在这里插入图片描述

例如如下最大堆与最小堆：
在这里插入图片描述
关于堆的有序性，可以看出来从根节点到任意结点路径上结点序列的有序性。

堆的抽象数据类型描述

在这里插入图片描述
最小堆和最大堆类似，这里就以最大堆为例进行介绍

最大堆的操作

最大堆的创建

typedef struct HeapStruct *MaxHeap;
struct HeapStruct {
    
	ElementType *Elements; /* 存储堆元素的数组 */
	int Size; /* 堆的当前元素个数 */
	int Capacity; /* 堆的最大容量 */
};

MaxHeap Create( int MaxSize )
{
     /* 创建容量为MaxSize的空的最大堆 */
	MaxHeap H = malloc( sizeof( struct HeapStruct ) );
	H->Elements = malloc( (MaxSize+1) * sizeof(ElementType));
	H->Size = 0;
	H->Capacity = MaxSize;
	H->Elements[0] = MaxData; 
	 /* 定义“哨兵”为大于堆中所有可能元素的值，便于以后更快操作 */
	return H;
}

创建的堆从下标为1的位置正式存放堆的元素，下标为0的位置不存放堆的元素，存放的是最大值，用作哨兵。从下标为1的位置存放元素也便于后续的一些求孩子结点等的操作。

最大堆的插入

对于最大堆的结点插入，直接插入结点是将结点放到完全二叉树表示的数组的最后面。而结点放入后需要保证有序性，这就要求该算法在插入结点后仍满足最大堆的特点。
例如：插入结点20，插入后满足完全二叉树，而且满足有序性。
在这里插入图片描述
例如：插入35，插入后满足完全二叉树，但是有序性被破坏，但是二者位置交换就满足有序性。
在这里插入图片描述
例如：插入58，插入后满足完全二叉树，但是有序性被破坏，58>31，二者交换，58>44，在进行交换，此时有序性满足。
在这里插入图片描述
综上得到最大堆插入结点的算法：
在这里插入图片描述
首先判断堆是否满，不满的话，插入结点令堆size++，然后判断当前结点的父结点是否比插入的值小，如果比当前插入结点的值小，就将父节点的值赋值给当前结点，然后令当前结点指向其父结点，继续上述判断，直到当前结点的父结点比要插入的值大，然后退出循环。将要插入的值赋给当前结点。

注意：H->Elements[0]是哨兵元素，它的值大于堆中最大值，因此可以控制循环结束。

经过上述过程，可以看出插入操作的时间复杂性等于树的高度，为logn

最大堆的删除

最大堆的删除，主要是指取出根结点(最大值)元素，同时删除堆的一个结点。
例如：删除58
在这里插入图片描述
删除58这个结点之后，为了满足完全二叉树的特性，将31这个结点替补到根节点处
在这里插入图片描述
替补上去之后，有序性还不能满足。此时将31的左右两个儿子中的最大值与31进行比较，如果比31大，则二者交换位置。
在这里插入图片描述
而此时有序性还不满足，再继续将31与两个儿子中的最大值比较，如果比31大，就交换。
在这里插入图片描述
此时，有序性满足。

经过上述过程，可以看出删除操作的时间复杂性等于树的高度，为logn

综上得到最大堆删除操作的算法：
在这里插入图片描述

  • 首先判断最大是否为空，不空的话才可删除。
  • 取出根节点（最大值）maxitem，然后将堆的最后一个值temp取出，同时令堆的size减1，因为将最大值点删除了。
  • 然后初始化parent=1，并判断parent结点是否有左儿子（利用parent*2<=H->size判断），如果有，则判断parent是否有右儿子(利用child！=H->size判断)，如果有右儿子，则令child指向左右儿子中最大的结点。如果最后一个堆结点的值temp比child的值大，则找到了temp要放的位置。如果最后一个堆结点的值temp比child的值小，则将child的值赋给parent，然后令parent等于child继续上述判断。

删除操作的大致思想就是，将最后一个结点替补根节点的位置，然后为了保证堆的有序性，依次向下与其儿子结点比较交换，直至有序性满足。

最大堆判空

bool IsEmptyHp(MaxHeap H)
{
    
     return (H->Size == 0);
}

最大堆判满

bool IsFull(MaxHeap H)
{
    
     return (H->Size == H->Capacity);
}

最大堆的建立

方法1：通过插入操作，将n个结点一个个插入到初始为空的堆中，时间代价为O(nlogn)

方法2：在O(n)的代价下建立最大堆（堆排序的一个步骤）

  • 将n个元素按输入顺序存入，先满足完全二叉树的结构特性
  • 然后调整各节点的位置，以满足最大堆的有序性

其实方法二借鉴了删除堆结点的操作，删除根节点之后，此时根节点的左子树是个堆，右子树是个堆，然后将最后一个结点替换跟结点，然后进行调整使其保证有序性。

根据方法二，首先建立这个堆：
在这里插入图片描述
我们从最右端有儿子的结点87，30，83开始（从倒数第二层最右端开始，从右往左，从下向上），依次借鉴删除堆结点将最后一个结点替换根节点，然后调整使其保证有序性的操作，调整使其满足有序性。
在这里插入图片描述
此时我们得到如下的堆
在这里插入图片描述
接下来我们再对66，43重复上述的操作
在这里插入图片描述
此时得到如下的堆，然后再对79重复上述操作过程
在这里插入图片描述
最终得到如下的堆：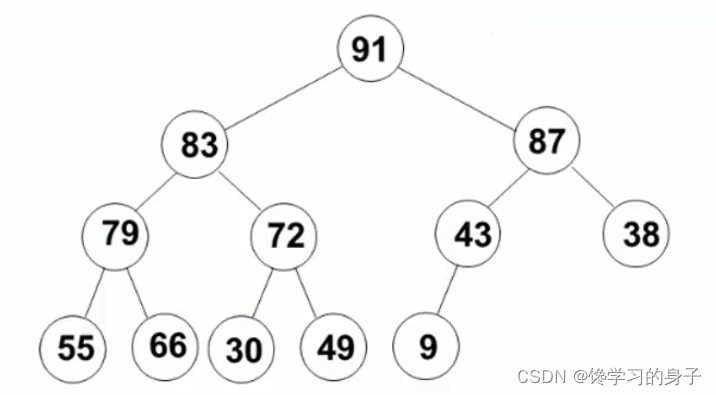
在这里插入图片描述

// 对结点进行堆排序，使其满足有序性的函数
void sortHp(MaxHeap H, int i)
{
    
     int child, parent;
     int temp = H->Elements[i];
     for(parent=i; parent*2 <= H->Size; parent=child)
     {
    
          child = 2 * parent;
          //如果有右儿子，并且右儿子更大
          if((child != H->Size) && H->Elements[child+1] > H->Elements[child])
               child+=1;
          if(H->Elements[child] < temp)  //左右儿子中最大值比父节点小
               break;
          else:
               H->Elements[parent] = H->Elements[child]; //将最大的儿子节点值赋给父节点
     }
     H->Elements[parent] = temp;

}

// 对堆中的结点从倒数第二层开始，从下往上，从右往左对每个结点都进行堆排序使其满足有序性
void adjust(MaxHeap H)
{
    
     int i = H->Size/2;
     for(; i>0; i--)
     {
    
          sortHp(H, i);
     }
}

时间复杂度的计算：
假设树的高度为k，树的节点数加1等于n，对于第i层节点需要交换的次数为： 2 i − 1 ∗ ( k − i ) 2^{i - 1} * (k - i) 2i−1∗(k−i)
在这里插入图片描述
建完堆之后，我们就依次删除堆的根节点，然后放入数组中，这就对应于堆排序，建堆的时间复杂度是O(n)，删除堆节点的时间复杂度是O(logn)，对n个节点都执行删除操作，所以删除操作总的时间复杂度是O(nlogn)，最终堆排序的时间复杂度是O(nlogn)。

完整代码：

#include<stdio.h>
#include<malloc.h>
#define bool int
#define MaxData 1000

typedef int ElementType;
typedef struct HeapStruct *MaxHeap;
struct HeapStruct{
    
     ElementType *Elements;
     int Size;
     int Capacity;
};

MaxHeap Create(int Maxsize);
bool IsFull(MaxHeap H);
bool IsEmptyHp(MaxHeap H);
void InsertItem(MaxHeap H, ElementType item);
ElementType DeleteMax(MaxHeap H);
void LevelOrderTraversal(MaxHeap H);  // 层次遍历

//第二种方式建立堆
void sortHp(MaxHeap H, int i);
void adjust(MaxHeap H);

int main(void)
{
    
     MaxHeap h = Create(5);
     printf("堆是否空：%d\n", IsEmptyHp(h));
     printf("堆是否满：%d\n", IsFull(h));
     //第一种方式建立堆
     InsertItem(h, 58);
     InsertItem(h, 44);
     InsertItem(h, 25);
     InsertItem(h, 35);
     InsertItem(h, 31);
      printf("堆是否满：%d\n", IsFull(h));
     LevelOrderTraversal(h);

     DeleteMax(h);
     LevelOrderTraversal(h);

     //第二种方式建立堆
     MaxHeap h2 = Create(12);
     h2->Size = 12;
     int item[12] = {
    79, 66, 43, 83, 30, 87, 38, 55, 91, 72, 49, 9};
     for(int i=1; i <= 12; i++)
     {
    
          h2->Elements[i] = item[i-1];
     }
     LevelOrderTraversal(h2);
     adjust(h2);
     LevelOrderTraversal(h2);
}
void sortHp(MaxHeap H, int i)
{
    
     int child, parent;
     int temp = H->Elements[i];
     for(parent=i; parent*2 <= H->Size; parent=child)
     {
    
          child = 2 * parent;
          if((child != H->Size) && H->Elements[child+1] > H->Elements[child])
               child+=1;
          if(H->Elements[child] < temp)
               break;
          else
               H->Elements[parent] = H->Elements[child];
     }
     H->Elements[parent] = temp;

}
void adjust(MaxHeap H)
{
    
     int i = H->Size/2;
     for(; i>0; i--)
     {
    
          sortHp(H, i);
     }
}

bool IsFull(MaxHeap H)
{
    
     return (H->Size == H->Capacity);
}

bool IsEmptyHp(MaxHeap H)
{
    
     return (H->Size == 0);
}
MaxHeap Create(int Maxsize)
{
    
     MaxHeap H = malloc(sizeof(struct HeapStruct));
     H->Elements = malloc((Maxsize + 1) * sizeof(ElementType));
     H->Size = 0;
     H->Capacity = Maxsize;
     H->Elements[0] = MaxData;
     return H;
}

void InsertItem(MaxHeap H, ElementType item)
{
    
     int i;
     if(IsFull(H))
     {
    
          printf("最大堆满");
          return;
     }
     i = ++H->Size;
     for(; H->Elements[i/2] < item; i/=2)
     {
    
          H->Elements[i] = H->Elements[i/2];
     }
     H->Elements[i] = item;
}

ElementType DeleteMax(MaxHeap H)
{
    
     int parent, child;
     ElementType MaxItem, temp;
     if (IsEmptyHp(H))
     {
    
          printf("最大堆已空");
          return 0;
     }
     MaxItem = H->Elements[1];  //记录下最大值点，最后返回

     //用最大堆中的最后一个元素从根节点开始向上过滤下层结点
     temp = H->Elements[H->Size];
     H->Size--;  //删除掉最大值，然后size-1
     for(parent=1; parent*2 <= H->Size; parent=child)
     {
    
          child = parent*2;
          if((child!=H->Size) && (H->Elements[child] < H->Elements[child+1]))
               child++;
          if(temp >= H->Elements[child]) break;
          else
               H->Elements[parent] = H->Elements[child];
     }
     H->Elements[parent] = temp;
     return MaxItem;

}
void LevelOrderTraversal(MaxHeap H)
{
    
     for(int i=1; i<=H->Size; i++)
          printf("%d ", H->Elements[i]);
     printf("\n");

}

在这里插入图片描述

原网站

版权声明
本文为[馋学习的身子]所创，转载请带上原文链接，感谢
https://freeline.blog.csdn.net/article/details/123502085

边栏推荐

猜你喜欢

随机推荐