当前位置:网站首页>[combinatorics] Introduction to Combinatorics (combinatorial thought 2: mathematical induction | mathematical induction promotion | multiple induction thought)
[combinatorics] Introduction to Combinatorics (combinatorial thought 2: mathematical induction | mathematical induction promotion | multiple induction thought)
2022-07-03 09:38:00 【Programmer community】
List of articles
- One 、 Combination thought 2 : Mathematical induction
- Two 、 Generalization of mathematical induction
- 3、 ... and 、 Multiple inductive thoughts
One 、 Combination thought 2 : Mathematical induction
Mathematical induction describe A proposition related to natural numbers
P
(
n
)
P(n)
P(n) ,
According to different questions , Set up
n
n
n The minimum value , Usually from
0
0
0 Start ,
1. The proof is divided into the following two steps :
( 1 ) Inductive basis : First prove that Inductive basis , If it is proved that
P
(
0
)
P(0)
P(0) It's true ;
( 2 ) Induction steps : according to Types of mathematical induction , Prove in different ways , Here you are First, mathematical induction and Second, mathematical induction Two kinds of induction ;
2. Mathematical induction :
( 1 ) First, mathematical induction : from
P
(
n
)
P(n)
P(n) deduction
P
(
n
+
1
)
P(n + 1)
P(n+1)
P
(
0
)
P(0)
P(0) It's true
hypothesis
P
(
n
)
P(n)
P(n) It's true , prove
P
(
n
+
1
)
P(n + 1)
P(n+1) It's true
( 2 ) Second, mathematical induction : All less than
n
n
n Of
P
(
0
)
,
P
(
1
)
,
⋯
,
P
(
n
−
1
)
P(0) , P(1), \cdots , P(n-1)
P(0),P(1),⋯,P(n−1) It's all true , deduction
P
(
n
)
P(n)
P(n) It's true ;
P
(
0
)
P(0)
P(0) It's true
Assume that all are less than
n
n
n The natural number of
k
k
k , proposition
P
(
k
)
P(k)
P(k) It's all true , namely
P
(
0
)
,
P
(
1
)
,
⋯
,
P
(
n
−
1
)
P(0) , P(1), \cdots , P(n-1)
P(0),P(1),⋯,P(n−1) It's all true , deduction
P
(
n
)
P(n)
P(n) It's true ;
Symbolized as :
P
(
0
)
∧
P
(
1
)
∧
⋯
∧
P
(
n
−
1
)
→
P
(
n
)
P(0) \land P(1) \land \cdots \land P(n-1) \to P(n)
P(0)∧P(1)∧⋯∧P(n−1)→P(n)
Two 、 Generalization of mathematical induction
Mathematical induction can be extended , There may be Two problems of natural numbers , therefore The corresponding proposition is two natural numbers
P
(
m
,
n
)
P(m,n)
P(m,n) , The previous proposition is a natural number
P
(
n
)
P(n)
P(n) ;
1. Prove the proposition of two natural numbers
P
(
m
,
n
)
P(m,n)
P(m,n)
For this
m
,
n
m,n
m,n Two natural numbers ,
Any given natural number
m
m
m , namely
m
m
m It can be a natural number of any size , Yes
n
n
n inductive ;
or
Any given natural number
n
n
n , namely
n
n
n It can be a natural number of any size , Yes
m
m
m inductive ;
Specify the value of a natural number first , Summarize another natural number ;
The induction of a natural number , The traditional mathematical induction method is used for induction and proof ;
2. Multiple induction :
( 1 ) Inductive basis : Set up
P
(
m
,
n
)
P(m,n)
P(m,n) One of the natural numbers is
0
0
0 , Another natural number is any size ;
P
(
0
,
n
′
)
P(0, n')
P(0,n′) Is the basis of induction ,
m
=
0
m= 0
m=0 ,
n
′
n'
n′ Is any size ;
P
(
m
′
,
0
)
P(m', 0)
P(m′,0) Is the basis of induction ,
n
=
0
n= 0
n=0 ,
m
′
m'
m′ Is any size ;
First prove that the above inductive basis is true ;
( 2 ) Induction steps :
hypothesis
P
(
m
−
1
,
n
)
P(m-1, n)
P(m−1,n) ,
P
(
m
,
n
−
1
)
P(m , n-1)
P(m,n−1) It's true , prove
P
(
m
,
n
)
P(m, n)
P(m,n) It's true ;
3、 ... and 、 Multiple inductive thoughts
Plane coordinate system :
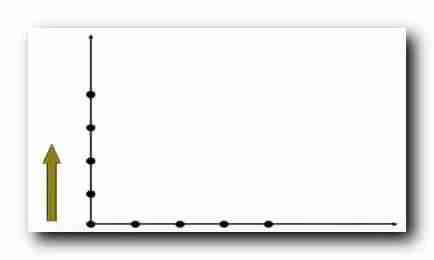
If
x
=
0
x = 0
x=0 When the parameter is true , namely
y
y
y On axis Dot represents All parameters are true ;
If
y
=
0
y = 0
y=0 When the parameter is true , namely
x
x
x On axis Dot represents All parameters are true ;
The points on the above two coordinate axes are equivalent to the basis of induction ;
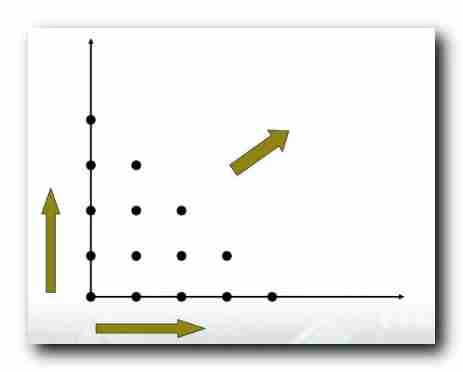
With the basis of induction , Use the point on the coordinate axis , The parameter represented by the point in the middle part of the derived coordinate system is true ;
Two points are true , Prove more than these two points
1
1
1 The point of is true , testify ,
hypothesis
P
(
m
−
1
,
n
)
P(m-1, n)
P(m−1,n) ,
P
(
m
,
n
−
1
)
P(m , n-1)
P(m,n−1) prove
P
(
m
,
n
)
P(m, n)
P(m,n) It's true
prove
P
(
1
,
1
)
P(1, 1)
P(1,1) It's true :
P
(
1
−
1
,
1
)
,
P
(
1
,
1
−
1
)
P(1 - 1 , 1) , P(1 , 1 - 1)
P(1−1,1),P(1,1−1) It's true , namely
P
(
0
,
1
)
,
P
(
1
,
0
)
P(0,1) , P(1, 0)
P(0,1),P(1,0) It's true ,
Can be derived
P
(
1
,
1
)
P(1,1)
P(1,1) It's true ;

At this time in
(
0
,
2
)
,
(
1
,
1
)
,
(
2
,
0
)
(0,2) , (1,1) , (2, 0)
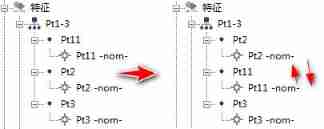
(0,2),(1,1),(2,0) The dots on the slash are all true , That is, the dot in the red box above ;
According to the point on the slash above, it can be proved Next jump on the slash The point of
(
0
,
3
)
,
(
1
,
2
)
,
(
2
,
1
)
,
(
3
,
0
)
(0, 3) , (1, 2) , (2, 1) , (3, 0)
(0,3),(1,2),(2,1),(3,0) The dot on the slash is true ;
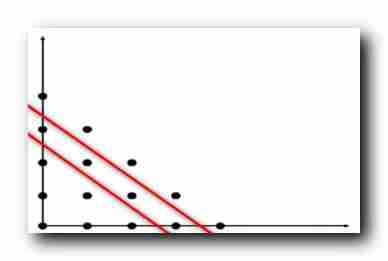
At this time, after the proof , The dots in the red box above are all true ;
Finally prove all the slashes ( top left corner -> The lower right corner ) All points on the are true ;
边栏推荐
- PolyWorks script development learning notes (I) - script development environment
- Analysis of the implementation principle of an open source markdown to rich text editor
- [CSDN]C1训练题解析_第三部分_JS基础
- LeetCode每日一题(2212. Maximum Points in an Archery Competition)
- Leetcode daily question (1856. maximum subarray min product)
- Desktop icon recognition based on OpenCV
- 从0开始使用pnpm构建一个Monorepo方式管理的demo
- LeetCode每日一题(2232. Minimize Result by Adding Parentheses to Expression)
- 2021-09-26
- Failed building wheel for argon2 cffi when installing Jupiter
猜你喜欢
PolyWorks script development learning notes (II) -treeview basic operations
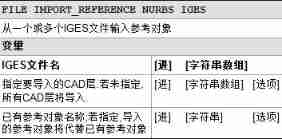
PolyWorks script development learning notes (4) - data import and alignment using file import
PolyWorks script development learning notes (III) -treeview advanced operation
![[csdn] C1 analyse des questions de formation Partie III Bar _ JS Foundation](/img/b2/68d53ad09688f7fc922ac65e104f15.png)
[csdn] C1 analyse des questions de formation Partie III Bar _ JS Foundation

LeetCode每日一题(2212. Maximum Points in an Archery Competition)

Hudi 数据管理和存储概述
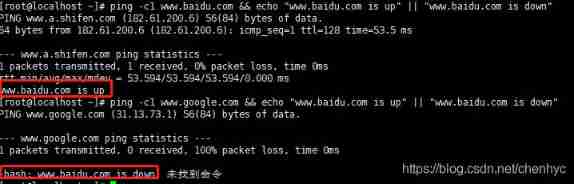
Shell logic case

Leetcode daily question (2090. K radius subarray averages)

Win10 install elk
Analysis of the implementation principle of an open source markdown to rich text editor
随机推荐
Spark 结构化流写入Hudi 实践
Analysis of the implementation principle of an open source markdown to rich text editor
Trial of the combination of RDS and crawler
Integrated use of interlij idea and sonarqube
Leetcode daily question (985. sum of even numbers after queries)
Hudi learning notes (III) analysis of core concepts
Learning C language from scratch -- installation and configuration of 01 MinGW
DSP data calculation error
Common software open source protocols
Leetcode daily question (2232. minimize result by addressing parents to expression)
IDEA 中使用 Hudi
Logstash+jdbc data synchronization +head display problems
Leetcode daily question (516. long palindromic subsequence)
numpy. Reshape() and resize() functions
The number of weak characters in the game (1996)
Win10安装ELK
Convert IP address to int
Win10 quick screenshot
Jetson nano custom boot icon kernel logo CBOOT logo
Find all possible recipes from given supplies