QT based "synthetic watermelon" game

Resource download address ：https://download.csdn.net/download/sheziqiong/85788271
Resource download address ：https://download.csdn.net/download/sheziqiong/85788271

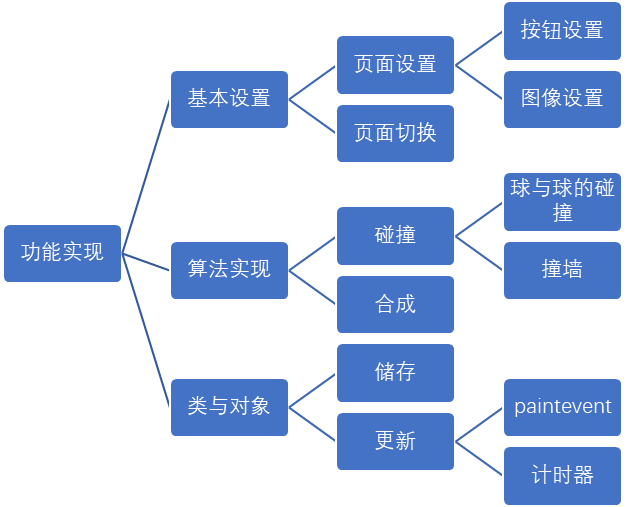
Main process

Overall process

Realize the idea : By opening Mainscene Interface , Define fruits fruit, Implement various operations .

Algorithm or formula

The core algorithm ： Two dimensional collision

principle ： Because two balls collide , The velocities on the tangent are parallel to each other , There is no force and the connecting lines collide with each other ( As shown in the figure below ), There will be forces , So we just need to find the ball 1 And the ball 2 The velocity in the direction of the centreline of . Then, according to the law of conservation of momentum and the law of conservation of mechanical energy, we can find the ball after collision 1 And the ball 2 The direction of the connecting center line of . Finally, by adding their respective velocities on the tangent to each other, we can get their respective velocities after collision x Speed ,y Speed .

and v1t : It's the ball 1 The projection speed in the direction of the connecting center line and the tangent line

and v2t : It's the ball 2 The projection speed in the direction of the connecting center line and the tangent line

The ball 1 The direction of the speed , be equal to v1n + v1t

The ball 2 The direction of the speed , be equal to v2n + v2t

distance = Math.sqrt(Math.pow((ball1.pointX - ball2.pointX),2) + Math.pow((ball1.pointY - ball2.pointY),2));
radius = ball1.r + ball2.r;
dx = ball1.pointX - ball2.pointX
     dy = ball1.pointY - ball2.pointY
          ex = dx / radius;
ey = dy / radius;       //  Get the unit vector of the centerline （ex,ey）
    = ex * ball1.vx + ey * ball1.vy
      = ex * ball2.vx + ey * ball2.vy

’ : The ball 1 The direction of velocity after the collision , be equal to v1n’ + v1t
’ : The ball 2 The direction of velocity after the collision , be equal to v2n’ + v2t
‘ and v2n’ :
Projection velocity of two small balls after collision

If the two balls are the same size , v1n’ and v2n’ The value is :

’ = v2n
’ = v1n

And according to the law of conservation of momentum and the law of conservation of mechanical energy :

and v2 : Speed before two balls hit .

and m2 : The mass of the two balls

' and v2' :
 The speed of the two balls after they hit each other 
double ux=-dy/distance,uy=dx/distance;// Tangential unit vector (ux,uy), Direction is (ex,ey) Counter clockwise rotation π/2
// The velocity projection of the ball in the direction of the line between the two balls is v=(vx,vy)·(ex,ey)
double v1=ex*balls[i].vx+ey*balls[i].vy;//i Normal velocity of 
double v2=ex*balls[j].vx+ey*balls[j].vy;//j Normal velocity of 
if (v2<v1) continue;// Two balls passed by , No collision 
// The velocity projection of the ball in the tangent direction is v'=(vx,vy)·(ux,uy)
double v11=ux*balls[i].vx+uy*balls[i].vy;//i Tangential velocity of 
double v22=ux*balls[j].vx+uy*balls[j].vy;//j Tangential velocity of 
// According to the conservation of momentum and kinetic energy theorem, the velocity in the direction of the connecting line between the two balls after collision is calculated u1 and u2, among K Indicates the degree of kinetic energy loss 
double m1=balls[i].mass,m2=balls[j].mass;
double u1=K*((m1-m2)*v1+2*m2*v2)/(m1+m2);//i Normal velocity after collision 
double u2=K*((m2-m1)*v2+2*m1*v1)/(m1+m2);//j Normal velocity after collision 

velocity vector (vx,vy)=(u1ex+v11ux,u1ey+v11uy)·(i,j)

balls[i].vx=1*(u1*ex+v11*ux);
balls[i].vy=1*(u1*ey+v11*uy);
balls[j].vx=1*(u2*ex+v22*ux);
balls[j].vy=1*(u2*ey+v22*uy);

Synthesis algorithm

combine(int i, int j)
{
    Ball b;
    initball(balls[i].type+1);
    double vi=sqrt(balls[i].vx*balls[i].vx+balls[i].vy*balls[i].vy);
    double vj=sqrt(balls[j].vx*balls[j].vx+balls[j].vy*balls[j].vy);
    if (vi<vj)// The position of the composite is the ball with lower speed 
    {
            =b._x=balls[i].x;
            =b._y=balls[i].y;
    }
    else {
            =b._x=balls[j].x;
            =b._y=balls[j].y;
    }
    vx=(balls[i].vx+balls[j].vx)/2.0;
    vy=(balls[i].vy+balls[j].vy)/2.0;
    ay=1;
    falling=1;
    balls[i]=b;     // Replace the new ball with balls[i]
    collideWall(i);
    balls[j]=balls[balls.size()-1];
    balls.pop_back();   // from balls Delete in array balls[j]
    gamescore+=2*balls[i].type;
    str.sprintf("score:%d",gamescore);
    q->setText(str);
}

Harvest

unit testing

（ Start interface ）

（ Game pause ）

（ The game is in progress ）

Resource download address ：https://download.csdn.net/download/sheziqiong/85788271
Resource download address ：https://download.csdn.net/download/sheziqiong/85788271