当前位置:网站首页>动态规划/斐波那契数列
动态规划/斐波那契数列
2022-06-09 02:27:00 【xcrj】
动态规划
存储结构:存储运行过程中的结果
- 动态规划数组
3个使用前提:
- 最优性原理:求解子问题等价于求解大问题
- 无后效性:后面的操作不会影响前面的结果
- 重叠子问题:非必要条件,使用递归求解斐波那契数列时,由于存在重叠子问题造成重复计算
使用递归求解斐波那契数列时,由于存在重叠子问题造成重复计算
- 重叠子问题,第3个项的解=前两项之和,
- 递归解决,造成重复计算
- 动态规划解决,由于使用了动态规划数组,存储了运算过程中的解,不会有重复计算
斐波那契
- Fibonacci数列
- f(0)=0
- f(1)=1
- f(n)=f(n-1+f(n-2)
代码
package xcrj.kchalgorithm.dynamicPrograming;
/** * Fibonacci数列 * f(0)=0 * f(1)=1 * f(n)=f(n-1+f(n-2) * <p> * 动态规划法 * 运行过程存储结构:动态规划数组 * <p> * 3个前提: * 1. 最优性原理:对子问题的求解等价于对大问题的求解 * 2. 无后效性:后面的操作不会影响前项的值 * 3. 存在重叠子问题(非必要条件):前2个数之和是第3个数的值 * <p> * 解法: * 1. 顺序解法:fibonacci是顺序解法 * 2. 逆序解法 */
public class Fibonacci {
// 存储结构 动态规划数组
private static int[] dynamicPrograming;
// 累计运行次数
private static int count = 1;
/** * 动态规划求解斐波那契数列 * * @param n 数列的第n个数 */
public static void fibonacci(int n) {
dynamicPrograming = new int[n];
dynamicPrograming[0] = 1;
dynamicPrograming[1] = 1;
for (int i = 2; i < n; i++) {
dynamicPrograming[i] = dynamicPrograming[i - 1] + dynamicPrograming[i - 2];
}
System.out.println(dynamicPrograming[n - 1]);
}
public static void main(String[] args) {
fibonacci(6);
}
}
边栏推荐
- 杰理之关于 SPI 主机配置参数的几个说明:【篇】
- "The original, skillful and vulgar skills of cloud native" -- composition of Volume I of the national new college entrance examination in 2022
- Interface test series - interface test practice of transfer transaction business scenarios
- Suppress status error LNK1104 failed to open the file "boost_thread-vc142-mt-gd-x64-1\u 79.lib"
- Designer must have design navigation website
- 蓝桥杯_青蛙的约会_扩展欧几里得
- export相關知識
- Exporter les connaissances pertinentes
- Buffett's alpha -- part of the code
- Jerry last IO_ Key how to use double keys? [chapter]
猜你喜欢

S系列·删除文件夹的几种姿势

进程与线程

21、ADS使用记录之E类功放设计(中)

Blue Bridge Cup_ Multiple problem_ stack_ Remainder

Using redis in business code to achieve caching effect
![[high level knowledge] epoll implementation principle of user mode protocol stack](/img/bc/f1d8ab69145ff5f644529e292dc5d5.png)
[high level knowledge] epoll implementation principle of user mode protocol stack
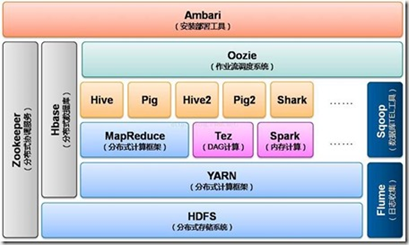
Basic architecture of data Lake

One month soft test | experience sharing of intermediate test for software designers (with learning materials)

【编码推流】SRS流媒体服务器安装及使用

Binary tree chain structure
随机推荐
Binary tree chain structure
[high level knowledge] epoll implementation principle of user mode protocol stack
【编码推流】SRS流媒体服务器安装及使用
[Tianyi cup 2021]esay_ eval
Immediate consumption: spare no effort to crack down on credit investigation and repair, and radical cure of chaos calls for social synergy
SQLite3 syntax (2)
toggleRowSelection()失效的2個重要影響因素
杰理之关于 SPI 主机配置参数的几个说明:【篇】
toggleRowSelection()失效的2个重要影响因素
SEC asset management - swebui open source application solution
Template_ Gauss elimination
[MySQL from Xiaobai to expert] Part 6: transaction and JDBC programming in MySQL
Redis cluster setup
Live short video app development
Diffusion model has been very popular in the field of image generation recently. How do you think its popularity has begun to surpass Gan?
Diffusion model最近在圖像生成領域大紅大紫,如何看待它的風頭開始超過GAN?
CVE-2022-30525漏洞复现
Kubernetes scheduling framework extension point
How does the technical leader bring down a team?
Knowledge points of 2022 information security engineer examination: configuration and use of network security products