Real topic of the 13th provincial competition of the Blue Bridge Cup in 2022 - block painting

subject 2660:

Blue Bridge Cup 2022 True title of the 13th provincial competition in - Building block painting

The time limit : 1Sec Memory limit : 256MB Submit : 623 solve : 135

Title Description

Xiao Ming has recently become addicted to building block painting , There are two types of building blocks , Respectively I type （ The size is 2 Unit area ） and L type （ The size is 3 Unit area ）：

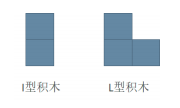
meanwhile , Xiao Ming has an area of 2 × N Canvas of , Canvas by 2 × N individual 1 × 1 Regional composition . Xiao Ming needs to fill the canvas with the above two kinds of building blocks , He wanted to know how many different ways there were ？ The building blocks can rotate freely , And the direction of the canvas is fixed .

Input

Enter an integer N, Represents the canvas size .

Output

Output an integer for the answer . Because the answer can be big , So output it to 1000000007 The value after taking the mold .

Sample input copy

3

Sample output copy

5

Tips

The five cases are shown in the figure below , The color is just to identify different building blocks ：

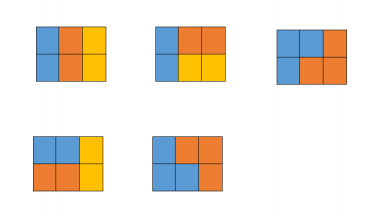
For all test cases ,1 ≤ N ≤ 10000000.

Their thinking :
Ah , However, when it is a game, it is impossible to measure another data , What a pity , But the idea is right when writing , unfortunately a[2][1] Write the wrong .

Ideas ：a[i][0]:i The stacking method of building blocks ,a[i][1]：i The stacking method of adding a small square .

Such as ：

perhaps

No matter how these three pieces are put , All call a[3][0].
If there is a small square on the right on this basis, it is called a[3][1], Note that the small square can be one row above the fourth column or one row below the fourth column （ If it's hard to find the picture, I won't give it , Imagine for yourself ）

The dynamic programming equation is given ：

 a[i][0]=(a[i-2][0]+a[i-2][1]+a[i-1][0])%mod; a[i][1]=(a[i-1][0]*2+a[i-1][1])%mod;

Canvas size is i The arrangement of , Both a[i][0] Value ：

1. Consider one less piece first I The arrangement of type a building blocks , Both a[i-1][0], Then add a piece I Type block is OK ,
2. Consider one less piece L The arrangement of type a building blocks , Both a[i-2][1], Then add a piece L Type block is OK ,
3. Consider two less I The arrangement of type a building blocks , Both a[i-2][0], Add two I Type building blocks , Be careful , Two pieces must be added horizontally , If it's vertical , It is equivalent to the first type of arrangement , repeated .
4. When it comes to missing more building blocks , You will find that no matter how you line up , The arrangement will repeat the above , in other words , The above three cases cover a[i][0] All the arrangements of .

So there is ：

a[i][0]=(a[i-2][0]+a[i-2][1]+a[i-1][0])%mod;

a[i][1] The arrangement of , You can draw and write by yourself .

Write the initial state ：

a[1][0]=1,a[2][0]=2,a[1][1]=2,a[2][1]=4;

Give the complete code ：

#include<stdio.h>#define mod 1000000007long int a[10000001][2];int main(){     int n;    a[1][0]=1,a[2][0]=2,a[1][1]=2,a[2][1]=4;    scanf("%d",&n);    if(n==1)printf("1");    else if(n==2)printf("2");    else {        for(int i=3;i<=n;i++){            a[i][0]=(a[i-2][0]+a[i-2][1]+a[i-1][0])%mod;            a[i][1]=(a[i-1][0]*2+a[i-1][1])%mod;        }        printf("%ld",a[n][0]%mod);    }    return 0;}

If you don't understand anything , You can comment or send me a private message ,
If it works for you , Just give this konjaku a good comment .