当前位置:网站首页>[hdu] P1466 计算直线的交点数
[hdu] P1466 计算直线的交点数
2022-06-22 09:18:00 【Lupin123123】
题目链接
组合数学题,考虑递推
如果要求n条直线中任意两条直线都有交点,设 a n a_n an为n条直线产生的交点数,那么易得 a n = a n − 1 + n − 1 a_n=a_{n-1}+n-1 an=an−1+n−1 因为把第n条直线加入到前n-1条直线的平面时,会与这n-1条直线都构成一个交点。
现在去掉“两两相交”条件,那么在加入第n条直线的时候就有直线与之平行,对交点数没有贡献。这启示我们从平行直线这个角度考虑问题。设 f ( i , j ) f(i,j) f(i,j)为有i条直线构成j个交点是否可行,前i-1条直线有k条与其平行, f ( i , j ) = 1 f(i,j)=1 f(i,j)=1当且仅当 f ( i − 1 − k , j − ( k + 1 ) ( i − 1 − k ) ) = 1 f(i-1-k,j-(k+1)(i-1-k))=1 f(i−1−k,j−(k+1)(i−1−k))=1时成立。
完整代码:
#include<bits/stdc++.h>
#define FAST ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define INF 0x3f3f3f3f
typedef long long ll;
const int maxn = 1e5+5;
using namespace std;
int n;
int dp[1001][1001];
int main()
{
FAST;
for (int i=1; i<=20; i++) dp[i][0]=1;
for (int i=2; i<=20; i++)
{
for (int j=1; j<=200; j++)
for (int k=0; k<=i-1; k++)
if (dp[i-1-k][j-(k+1)*(i-1-k)]) dp[i][j]=1;
}
while(cin>>n)
{
for (int i=0; i<=n*(n-1)/2-1; i++)
if (dp[n][i]) cout<<i<<' ';
cout<<n*(n-1)/2<<endl;
}
return 0;
}
边栏推荐
- Function summary (1)
- 经典&&案例
- MySQL field attribute list sends a document for future reference
- 800+ PHP grammar and words are proficient only after you have used them
- Alibaba big fish SMS interface PHP version, simplified version Alibaba big fish SMS sending interface PHP instance
- mknod
- .a文件链接库的使用
- Apprentissage automatique | nltk Erreur de téléchargement des données | solution d'erreur de téléchargement du corpus stopwords pour nltk
- Value (address) transmission, see the name clearly, don't fall into the ditch
- Performance optimization topics
猜你喜欢
![[network security officer] an attack technology that needs to be understood - high hidden and high persistent threats](/img/c9/c0ee95e816cac698f5397cc369d9ec.jpg)
[network security officer] an attack technology that needs to be understood - high hidden and high persistent threats

前馈和反向传播
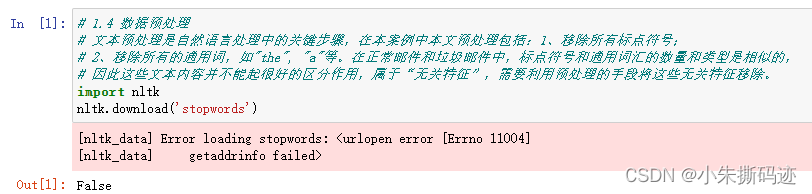
Apprentissage automatique | nltk Erreur de téléchargement des données | solution d'erreur de téléchargement du corpus stopwords pour nltk

Byte/byte? Don't get dizzy!

性能优化专题

It is hoped that more and more women will engage in scientific and technological work

Volumedetect of ffmpeg
![In the monorepo learning, execute NPM run build to report error[err\u require\esm] of ES module](/img/76/ec4776bcd452584290ef8bf5d0e06f.jpg)
In the monorepo learning, execute NPM run build to report error[err\u require\esm] of ES module

Debian10 LVM逻辑卷

C# 进程如何使用非静态方法
随机推荐
VMware installation Kali
Module usage of pytorch: linear model (incomplete)
Record some Oracle operation commands
Common SQL statements in MySQL
Two threads execute i++ 100 times respectively, and the possible values obtained
一文走近ZMQ
Summary and future prospect of transfer learning | community essay solicitation
DOM programming
通过docker安装mysql(5.7+8.0)并配置主从复制(GTID+增强半同步)
Redis 切片集群的数据倾斜分析
C language question brushing | three item operation to realize capital judgment (16)
Stream流创建_操作_收集_案例
Network security Kali penetration learning how to conduct Nessus vulnerability detection
Debian10安装Zabbix5.4
Overview of microservice architecture
前馈和反向传播
MySQL中常用的SQL语句
模糊查询和聚合函数
Unicode characters / static non static access
集合中的类--->你关注过那些是线程安全的吗?