【深度学习】：《PyTorch入门到项目实战》第八天：权重衰退（含源码）

• 本文收录于【深度学习】：《PyTorch入门到项目实战》专栏，此专栏主要记录如何使用PyTorch实现深度学习笔记，尽量坚持每周持续更新，欢迎大家订阅！
• 个人主页：JoJo的数据分析历险记
• 个人介绍：小编大四统计在读，目前保研到统计学top3高校继续攻读统计研究生
• 如果文章对你有帮助，欢迎关注、点赞、收藏、订阅专栏

参考资料：本专栏主要以沐神《动手学深度学习》为学习资料，记录自己的学习笔记，能力有限，如有错误，欢迎大家指正。同时沐神上传了的教学视频和教材，大家可以前往学习。

• 视频：动手学深度学习
• 教材：动手学深度学习

1.基本概念

前一节我们描述了过拟合的问题，虽然我们可以通过增加更多的数据来减少过拟合，但是成本较高，有时候并不能满足。因此现在我们来介绍一些正则化模型的方法。在深度学习中，权重衰退是使用较为广泛的一种正则化方法。具体原理如下。
我们引入L2正则化，此时我们的损失函数为：
$$\frac{1}{2m}\sum _{i=1}^n(W^T{X}^{(i)}+b-y^{(i)}{)}^2+\frac{\lambda }{2}||W|{|}^2$$
其中，$\frac{\lambda }{2}||W|{|}^2$称为惩罚项
对新的随时函数求梯度得到：
$$\frac{dL}{dw}+\lambda W$$
和我们之前更新参数一样，L2正则化回归的梯度下降更新如下：
$$w:=(1-\eta \lambda )w-\eta \frac{dL}{dw}$$
通常$\eta \lambda <1$，因此在深度学习中我们称为权重衰退。
注意事项：

• 1.我们只对权重W进行惩罚,而不对b进行惩罚
• 2.$\lambda$是一个超参数，值越大，则对权重的衰退越大，当趋近无穷时，权重趋近0，相反如果值为0，则没有约束。
• 3.L2正则化不能实现稀疏的结果，如果想要减少特征，使用L1正则化进行特征选择。
  下面通过具体代码来看看具体是如何实现的

2.代码实现

和上一章一样，照样使用模拟数据集，生成数据集如下：
$$y=0.1+\sum _{i=1}^{d}0.01x_i+ϵ\text{ where }ϵ\sim \mathcal{N}(0,0.01^2)$$

2.1 生成数据集

这里假设真实的数据如下：
$$y=0.1+\sum _{i=1}^{200}0.01x_i+ϵ$$
下面我们先生成数据集

"""导入相关库"""
import torch
from d2l import torch as d2l
from torch import nn
%matplotlib inline

# 定义相关函数。这是沐神教材中的函数，如果下载了d2l可以直接导入
def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))
def load_array(data_arrays, batch_size, is_train=True): 
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)#将数据转换为tensor
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

"""生成数据集"""
n_train, n_test, num_inputs, batch_size = 50, 100, 200, 5#定义相关训练集，验证集，输入变量，以及batch的大小
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.1#定义真实的参数
train_data = d2l.synthetic_data(true_w, true_b, n_train)#生成模拟数据，具体函数如下
train_iter = d2l.load_array(train_data, batch_size)#加载训练集数据
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)

根据上一章的介绍，我们知道样本越小越容易造成过拟合，这里我们将样本量设置为100，但是参数却有200个，这种情况下p>n,很容易造成过拟合现象。

2.2 初始化参数

生成数据集后，下一步就是初始化参数，这里我们对于权重$w$初始化为标准正态分布，偏差$b$初始化为0

def init_params():
    w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)#生成标准正态分布
    b = torch.zeros(1, requires_grad=True)#生成全部为0的数据
    return [w, b]

2.3 定义惩罚项

这里我们定义L2正则化,具体代码如下所示

def l2_penalty(w):
    return torch.sum(w.pow(2)) / 2

2.3 训练

这里和之前线性回归训练基本一致，唯一不同的是多了一个惩罚项，因此lambd为超参数

def train(lambd):
    w, b = init_params()#初始化参数
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss#这里使用匿名函数，定义了两个函数，一个是求解模型结果，一个是损失函数
    num_epochs, lr = 100, 0.003
    """定义相关图形设置"""
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    """模型训练，更新参数"""
    for epoch in range(num_epochs):
        for X, y in train_iter:
            # 增加了L2范数惩罚项，
            # 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
            l = loss(net(X), y) + lambd * l2_penalty(w)
            l.sum().backward()
            d2l.sgd([w, b], lr, batch_size)
        """绘制训练误差和测试误差"""
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数是：', torch.norm(w).item())

首先，我们来看看不增加惩罚项的情况，即和我们之前的线性回归一致，此时，存在严重的过拟合现象，如下图所示

train(lambd=0)

从上图结果来看，存在严重的过拟合问题，验证误差远远比训练误差大。下面我们来看看lambd为5的情况下的结果

train(lambd=5)

可以看出，随着lambd的增加，验证误差不断减少，但是还是存在过拟合。

def train_concise(wd):
    net = nn.Sequential(nn.Linear(num_inputs, 1))#定义线性神经网络
    for param in net.parameters():
        param.data.normal_()#初始化参数
    loss = nn.MSELoss(reduction='none')#定义MSE损失函数
    num_epochs, lr = 100, 0.003#定义训练次数和学习率
    # 偏置参数没有衰减
    trainer = torch.optim.SGD([
        {
    "params":net[0].weight,'weight_decay': wd},
        {
    "params":net[0].bias}], lr=lr)#定义权重衰退，其中超参数为wd
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])#绘图
    """训练模型"""
    for epoch in range(num_epochs):
        for X, y in train_iter:
            trainer.zero_grad()
            l = loss(net(X), y)
            l.mean().backward()
            trainer.step()
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1,
                         (d2l.evaluate_loss(net, train_iter, loss),
                          d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数：', net[0].weight.norm().item())

train_concise(0)

train_concise(3)

3.拓展部分

沐神的参考教材中使用的是L2正则化，我们接下来看看使用L1正则化的效果，首先需要定义一下L1正则化，如下所示：
$$\frac{1}{2m}\sum _{i=1}^n(W^T{X}^{(i)}+b-y^{(i)}{)}^2+\lambda |W|$$

def l1_penalty(w):
    return torch.sum(torch.abs(w))

def train_l1(lambd):
    w, b = init_params()#初始化参数
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss#这里使用匿名函数，定义了两个函数，一个是求解模型结果，一个是损失函数
    num_epochs, lr = 100, 0.003
    """定义相关图形设置"""
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    """模型训练，更新参数"""
    for epoch in range(num_epochs):
        for X, y in train_iter:
            # 增加了L1范数惩罚项，
            # 广播机制使l1_penalty(w)成为一个长度为batch_size的向量
            l = loss(net(X), y) + lambd * l1_penalty(w)
            l.sum().backward()
            d2l.sgd([w, b], lr, batch_size)
        """绘制训练误差和测试误差"""
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数是：', torch.norm(w).item())

train_l1(1)

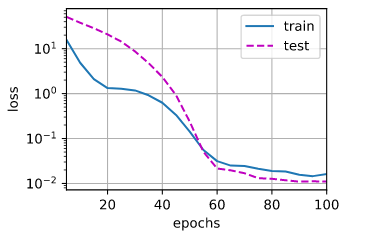
可以看出使用L1正则化，当lambd为1的时候，就可以使得验证误差基本等于训练误差。其实正如我们之前说的，L2正则化只能将参数压缩，但是不能去除为0，我们这个模拟数据集中，p为200，n为100，p>>n,此时使用L1正则化可以使得某些特征的系数为0，从而更好的缓解过拟合问题。

本章的介绍到此介绍，如果文章对你有帮助，请多多点赞、收藏、评论、关注支持！！