当前位置:网站首页>2021-08-12函数递归_和鹏哥学习C语言
2021-08-12函数递归_和鹏哥学习C语言
2022-07-26 10:36:00 【竹某】
目录
#1函数递归
函数递归指的是函数自己调用自己的技术。函数递归在思考方式上显得十分优雅,体现了将较大规模的问题转化为较低规模的同类问题的思想;但是从算法效率上讲,递归是一种效率较低的算法。
递归算法必需符合两个条件:1.有一个出口(一个最低规模的问题的解决方法);2.将较大规模的问题转化为较低规模的同类问题的方法。使用sequence的表述是:1.知道初始的几项(a0,a1,a2等);2.知道递推公式(an+1=f(an))。 这保证了递归不会无限地进行,也体现出了使用递归算法的函数结构,体现了递归算法的思维方式(降低问题规模&提供最低规模问题的解决方法)。
#2 函数递归的几个简单实例
//从高位到低位打印给定数字num的每一位
void print(int num) {
if (num <= 9 and num >= 0)//相当于是始项a0,为递归的出口
printf("%d ",num);
else {
print(num / 10);
printf("%d ", num % 10);//相当于是通项公式an=f(an-1)
}
return;
}
//打印1234
//=打印123+打印4
//=打印12+打印3+打印4
//=打印1+打印2+打印3+打印4
//打印1是最低规模的问题(打印一位数),等号两边体现了问题规模的降低//不使用临时变量,来计算给定字符串的长度
int my_strlen(char* str) {
if (*str == '\0')
return 0; //初始项,最低规模的问题
else {
return my_strlen(str+1)+1;//递推公式
}
}
//计算"China"的长度(指针指C)
//=计算hina的长度(指针右移指h)+1
//=计算ina的长度(指针右移指i)+1+1
//...
//=计算'\0'的长度(指针指'\0')+1+1+1+1+1
//计算'\0'的长度为最低规模的问题//计算斐波那契数列的第n项1 1 2 3 5 8 13...
int sequence(int n) {
if (n == 1 or n == 2) return 1;
else
return sequence(n - 1) + sequence(n - 2);
}
//数列的初始项和递推公式十分明显#3从计算斐波那契数列看递归算法的运算效率
计算a(50)需要计算a(49)和a(48),而计算a(49)又要计算a(48)和a(47)。a(48)被重复计算。同样,计算a(48)时,a(47)又被重复计算。如图:
a(50)
a(49)+a(48)
a(48)+a(47)+a(47)+a(46)
a(47)+a(46)+a(46)+a(45)+a(46)+a(45)+a(45)+a(44)
...
由此看来最初的几项会被反复计算很多次。
我们不妨计算以下计算a(40)时a(3)被计算的次数,这是由于计算a(50)往往要花上10min左右,而计算a(40)可能只需要10s左右。从这里也能看出递归算法的时间复杂度之差。更别说其空间复杂度了(递归算法常见的一个问题就是栈溢出)。
int count3_40 = 0;//使用斐波那契数列的递归算法求sequence(40)时sequence(3)计算的次数
int count30_40 = 0;//使用斐波那契数列的递归算法求sequence(40)时sequence(30)计算的次数
int sequence(int n) {
if (n == 3) ++ count3_40;
if (n == 30) ++count30_40;
if (n == 1 or n == 2) return 1;
else
return sequence(n - 1) + sequence(n - 2);
可以发现a(3)被反复计算了三千多万次。可见递归算法冗余度之高。
#4 迭代与递归
将计算斐波那契数列的递归算法改为迭代,即循环。
int sequence_loop(int n) {
int a = 1; //i
int b = 1; //i+1
int c = 0; //i+2
if (n <= 2) return 1;
for (int i = 3; i <= n;++i) {
c = a + b;
a = b;
b = c;
}
return c;
}
//先考虑实际应用场景,后考虑如何实现。称为TDD,测试驱动开发。
//递归包含了大量重复运算,运算效率很低。应该换为迭代(循环)。递归算法在思维方式上虽然优雅,但是确实在效率上不让人满意。既想要递归算法的简洁性,又想要迭代算法上的效率,就应该找到将递归算法改为迭代算法的一般方法。这个方法我在学习数据结构时遇到过。
#5 汉诺塔问题

图片截自 https://www.biancheng.net/algorithm/tower_of_hanoi.html
汉诺塔问题要求我们借助中间的柱子,将最左侧的n个由大到小的圆盘移到最右侧,并符合上述两个条件。
依照递归算法的思想,我们尝试降低n阶汉诺塔问题的规模。我们实际上可以不用管最大的那个盘子,而使另外n-1个盘子在从左到右三根柱子(分别命名为x,y,z)上按照规则随意移动。
所以将x上n个盘子移到z上——我们记为Hanoi(x,z,n)——可以转化为Hanoi(x,y,n-1)+Hanoi(x,z,1)+Hanoi(y,z,n-1)。这样问题的规模就得到了降低。
那么,汉诺塔问题的最简形式有无解呢?显而易见,是有的。即为:Hanoi(x,z,1)。
所以
Hanoi(x,z,1)
Hanoi(x,z,2)=Hanoi(x,y,1)+Hanoi(x,z,1)+Hanoi(y,z,1)
Hanoi(x,z,3)=Hanoi(x,y,2)+Hanoi(x,z,1)+Hanoi(y,z,2)
......
Hanoi(x,y,n-1)+Hanoi(x,z,1)+Hanoi(y,z,n-1)
那么如何在计算机上模拟柱子和盘子呢?可以使用数组(满足栈的特点且下标越大的元素数值越大)和由大到小的数字(1,2,3,......,n-1,n)。为了某些操作的方便起见,需要使用结构体(包含数组和柱子的其他属性)来表示柱子。
#define MAX 20
#include <stdio.h>
struct HanoiTower {
int num = 0;//汉诺塔中盘子的数量
int arr[MAX] = { 0 };//具有栈的特性,元素优先放入数组中下标大的位置
};
void generateHanoi(HanoiTower*, int);
void Hanoi(HanoiTower*, HanoiTower*,HanoiTower*, int);
int count = 0;//用于记录汉诺塔次数,为2^x-1
int main() {
HanoiTower x;
HanoiTower y;
HanoiTower z;
generateHanoi(&x,7);
Hanoi(&x,&z,&y,7);
return 0;
}
//汉诺塔问题生成器,用于初始化HanoiTower类型的变量
void generateHanoi(HanoiTower* m, int scale) {
//scale为问题规模
m->num = scale;
for (int i = MAX - 1; scale > 0 ; --i) {
m->arr[i] = scale;
scale--;
}
return;
}
//汉诺塔问题解决器,使用递归算法解决汉诺塔问题
//source源柱;dest目标柱;by经过柱
void Hanoi(HanoiTower* source, HanoiTower* dest,HanoiTower* by, int scale) {
if (scale == 1) {
dest->arr[MAX - 1 - (dest->num)] = source->arr[MAX - (source->num)];
source->arr[MAX - (source->num)] = 0;
(source->num)--;
(dest->num)++;
++count;
}
else {
Hanoi(source,by,dest,scale-1);
Hanoi(source,dest,by,1);
Hanoi(by,dest,source,scale-1);
}
return;
}
边栏推荐
猜你喜欢

.NET 开源框架在工业生产中的应用
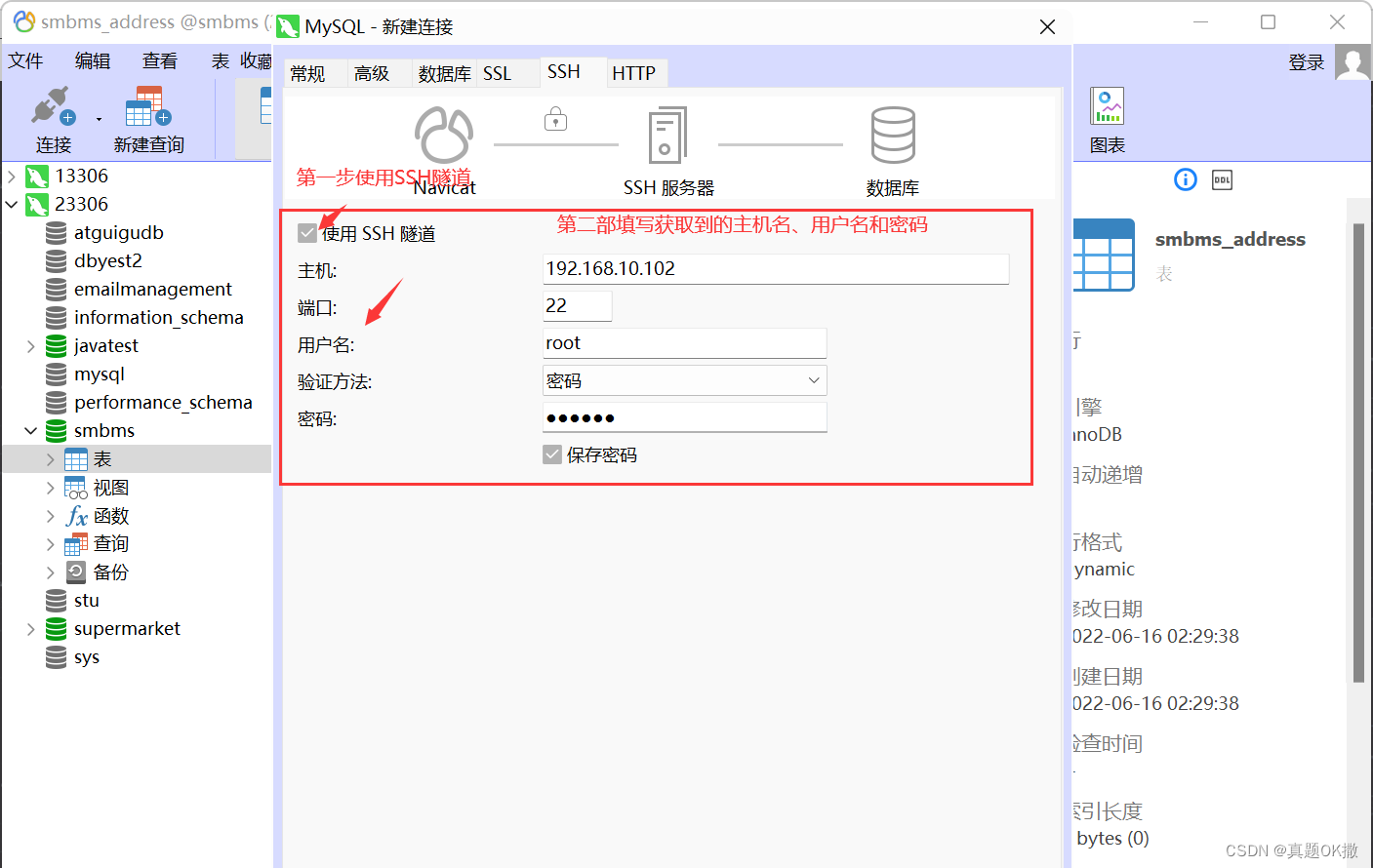
Navicat15 MySQL (centos7) connected to local virtual machine

码云,正式支持 Pages 功能,可以部署静态页面

【机器学习小记】【风格迁移】deeplearning.ai course4 4th week programming(tensorflow2)

Redis docker instance and data structure

英语基础句型结构------起源

多目标优化系列1---NSGA2的非支配排序函数的讲解

干货likeshop外卖点餐系统开源啦100%开源无加密

Introduction to data analysis | kaggle Titanic mission

el-table实现可编辑表格
随机推荐
Perfect / buffer motion framework in sentence parsing JS (for beginners)
异常的概念与处理
.net operation redis set unordered collection
Problems encountered in QRcode QR code (C language)
鹏哥C语言第四课(3)
码云,正式支持 Pages 功能,可以部署静态页面
Issue 6: which mainstream programming language should college students choose
JS对象赋值问题
父类对子类的引用(父类引用指向子类对象)
Introduction to data analysis | kaggle Titanic mission (I) - > data loading and preliminary observation
11 在 operator= 中处理“自我赋值”
Database functions
Introduction to data analysis | kaggle Titanic mission
el-table实现可编辑表格
[leetcode每日一题2021/2/13]448. 找到所有数组中消失的数字
Analyze the hybrid construction objects in JS in detail (construction plus attributes, prototype plus methods)
移动端H5开发常用技巧总结
Introduction to Phoenix (Level 1: Phoenix installation, level 2: Phoenix basic grammar)
.net operation redis string string
Uninstall Meizu app store