Dynamic programming-01 backpack, partition, etc. and subset, weight of the last stone

01 Fundamentals of knapsack problem

Reference resources https://www.programmercarl.com/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-1.html#%E4%BA%8C%E7%BB%B4dp%E6%95%B0%E7%BB%8401%E8%83%8C%E5%8C%85
problem ： Yes n Items and one can carry a maximum weight of w The backpack . The first i The weight of the item is weight[i], The value is value[i] . Each item can only be used once , Solve which items are loaded into the backpack, and the total value of the items is the largest .

1 determine dp The meaning of arrays and subscripts
For the knapsack problem , There is a way to write , It's using two-dimensional arrays , namely dp[i][j] Indicates from subscript [0-i] Take whatever you want from your belongings , Put in capacity j The backpack , What is the maximum total value
2 Recurrence 1 No objects i： from dp[i - 1][j] Introduction , The capacity of the backpack is j, There are no items in it i Maximum value of , here dp[i][j] Namely dp[i - 1][j].( It's actually when things i It weighs more than a backpack j When the weight of , goods i Can't put it in the backpack , So the value in the backpack is still the same as before .)

2 Put things i： from dp[i - 1][j - weight[i]] Introduction ,dp[i - 1][j - weight[i]] The capacity of the backpack is j - weight[i] Don't put things when you are i Maximum value of , that dp[i - 1][j - weight[i]] + value[i] （ goods i The value of ）, Is to put things in your backpack i Get the most value
So the recursive formula ： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

3 About initialization , Be sure to and dp The definition of the array matches , Otherwise, the recursive formula will become more and more chaotic .

First of all, from the dp[i][j] Starting from the definition of , If the backpack capacity j by 0 Words , namely dp[i][0], No matter what items you choose , The total value of the backpack must be 0. Pictured ：

dp[0][j], namely ：i by 0, Storage number 0 When you get your stuff , The maximum value that a backpack of each capacity can store .

1 So obviously when j < weight[0] When ,dp[0][j] Should be 0, Because the backpack has more capacity than the number 0 The weight of the goods is still small .

2 When j >= weight[0] when ,dp[0][j] Should be value[0], Because the backpack has enough capacity to put numbers 0 goods .

4 traversal order
First traversal Items or first traverse the weight of the backpack ？

In fact, it can be ！！ But it's better to traverse the items first .

// weight Size of array   Is the number of items 
for(int i = 1; i < weight.size(); i++) {
     //  Traverse the items 
    for(int j = 0; j <= bagweight; j++) {
     //  Traverse the backpack capacity 
        if (j < weight[i]) dp[i][j] = dp[i - 1][j]; 
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

    }
}

Why is it that items or backpacks can be used first ？
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); As can be seen from the recursive formula dp[i][j] Is to rely on dp[i-1][j] and dp[i - 1][j - weight[i]] Derived from .

dp[i-1][j] and dp[i - 1][j - weight[i]] All in dp[i][j] In the upper left corner of （ Including the positive direction ）, that Go through the items first , The process of traversing the backpack is shown in the figure

5 Give an example to deduce dp Array
Take a look at the corresponding dp The number of arrays , Pictured ：

# -*- codeing = utf-8 -*-
# @Time :2022/6/18 14:40
# @Author:sueong
# @File:01 knapsack .py
# @Software:PyCharm


def bagproblem(bag_size, weight, value):
    rows, cols = len(weight), bag_size + 1
    dp = [[0 for _ in range(cols)] for _ in range(rows)]

    # dp[i][j]  Indicates from subscript [0-i] Take whatever you want from your belongings , Put in capacity j The backpack , What is the maximum total value .
    #  initialization dp
    #  The first 0 The capacity of the backpack is listed as 0  So the value total=0
    for i in range(rows):
        dp[i][0] = 0
    first_item_weight, first_item_value = weight[0], value[0]
    #  Traverse No 0 That's ok   There's only one item   Compare the weight of the backpack with the weight of the object itself 
    for j in range(1, cols):
        if first_item_weight <= j:
            dp[0][j] = first_item_value

    #  to update dp Array : Go through the items first , And then traverse the backpack 
    for i in range(1, rows):
        for j in range(1, cols):
            # j Is the current backpack weight   If the weight is smaller than the current item   That means you can't choose 
            if j < weight[i]:
                dp[i][j] = dp[i-1][j]
            else:
                #  The first i Items   No election ,or  choose 
                dp[i][j] = max(dp[i-1][j], dp[i - 1][j - weight[i]] + value[i])
    print(dp, dp[-1][-1])
    return dp[-1][-1]


if __name__ == "__main__":
    bag_size = 4
    weight = [1, 3, 4]
    value = [15, 20, 30]
    bagproblem(bag_size, weight, value)

Compressed into a one-dimensional array

In fact, it can be found that if dp[i - 1] Copy that layer to dp[i] On , The expression can be ：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

Instead of putting dp[i - 1] Copy this layer to dp[i] On , Let's just use one-dimensional array , Only dp[j]（ One dimensional array , It can also be understood as a rolling array ）.

dp[i][j] Indicates from subscript [0-i] Take whatever you want from your belongings , Put in capacity j The backpack , What is the maximum total value .

dp[j - weight[i]] + value[i] Express Capacity of j - goods i weight The backpack add goods i The value of .（ That is, the capacity is j The backpack , Put something in i After that, the value is ：dp[j]）

here dp[j] There are two choices , One is to take yourself dp[j] amount to A two-dimensional dp Array dp[i-1][j], I.e. no objects i, One is to take dp[j - weight[i]] + value[i], That is to put things i, Specify the maximum , After all, it's for maximum value

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

dp When deriving an array, it must take the number with the largest value , If the value given by the title is a positive integer, then it is not 0 Subscripts are initialized to 0 That's all right. .

A one-dimensional dp Array traversal order

for(int i = 0; i < weight.size(); i++) {
     //  Traverse the items 
    for(int j = bagWeight; j >= weight[i]; j--) {
     //  Traverse the backpack capacity 
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

Traversal in reverse order is to ensure that items i Only once , Backpacks are from big to small

# -*- codeing = utf-8 -*-
# @Time :2022/6/18 14:40
# @Author:sueong
# @File:01 knapsack .py
# @Software:PyCharm


def bagproblem(bag_size, weight, value):
    n = bag_size + 1
    dp = [0] * n

    # dp[j]  The capacity is j The backpack , What is the maximum total value .
    #  initialization dp All for 0
    #  to update dp Array : Go through the items first , Then traverse the knapsack in reverse order 
    for i in range(len(weight)):
        #  because j-weight[i]>=0  therefore j>=weight[i]  You can only choose when the backpack capacity is greater than the current item weight   Because in reverse order   So it's time to weight[i] - 1 One in front of 
        for j in range(bag_size, weight[i] - 1, -1):
            dp[j] = max(dp[j], dp[j-weight[i]] + value[i])

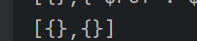
    print(dp, dp[-1])
    return dp[-1]


if __name__ == "__main__":
    bag_size = 4
    weight = [1, 3, 4]
    value = [15, 20, 30]
    bagproblem(bag_size, weight, value)

416. To divide into equal and subsets

The volume of the backpack is sum / 2
The goods to be put in the backpack （ The elements in the set ） Weight is The value of the element , The value is also the value of the element
If the backpack is just full , Indicates that the sum of sum / 2 Subset .
Every element in the backpack can't be put repeatedly .
After the above analysis , We can apply 01 knapsack , To solve this problem .

• determine dp The meaning of arrays and subscripts

01 In the backpack ,dp[j] Express ： Capacity of j The backpack , The value of the items carried can be up to dp[j].

Get to the point ,dp[j] Express The total capacity of the backpack is j, The maximum can be made up j The sum of the subsets of is dp[j].

• Determine the recurrence formula

01 The recurrence formula of knapsack is ：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

This topic , It's equivalent to putting values in your backpack , So the object i The weight of is nums[i], Its value is also nums[i].

So the recurrence formula ：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);

• dp How to initialize an array

stay 01 knapsack , A one-dimensional dp How to initialize , Already said ,

from dp[j] By definition , First dp[0] It must be 0.

If the value given by the topic is a positive integer, then it is not 0 Subscripts are initialized to 0 That's all right. , If the title gives a negative value , So no 0 The subscript is initialized to negative infinity .

• Determine the traversal order

//  Start  01 knapsack 
for(int i = 0; i < nums.size(); i++) {
    
    for(int j = target; j >= nums[i]; j--) {
     //  Each element must be non repeatable , So go from big to small 
        dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
    }
}

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        target = sum(nums)
        if target % 2 == 1: return False
        target //= 2
        dp = [0] * 10001
        #  The total capacity of the backpack is j, The maximum can be made up j The sum of the subsets of is dp[j]
        #  Traverse the goods in positive order （ Numbers ）  Traversal in reverse order consists of and （ Backpack Capacity ）
        for i in range(len(nums)):
            for j in range(target, nums[i]-1, -1):
                dp[j] = max(dp[j], dp[j-nums[i]] + nums[i])
        #  If dp[j] == j  explain , The sum of subsets in the set can be summed up  
        return target == dp[target]

1049. The weight of the last stone II

This question is actually Try to divide the stones into two piles of the same weight , The smallest stone left after the collision , This will dissolve into 01 It's a knapsack problem .

Is it the same as what was explained yesterday 416. To divide into equal and subsets (opens new window) It's very similar .

The weight of this item is store[i], The value of the goods is also store[i].

Corresponding 01 The weight of the items in the backpack weight[i] and Value of goods value[i].

In the calculation target When ,target = sum / 2 Because it's rounding down , therefore sum - dp[target] Must be greater than or equal to dp[target] Of .

class Solution:
    def lastStoneWeightII(self, stones: List[int]) -> int:
        total = sum(stones)
        target = sum(stones)
        target //= 2

        #  So the maximum weight is 30 * 1000 .
        # And what we ask for target In fact, it's only half the maximum weight , therefore dp Open the array to 15000 Just the size .

        dp = [0] * 15001

        # As far as possible, divide into two identical piles 
        # dp[j] The capacity is j The backpack , You can recite at most dp[j] Such a heavy stone .
        #  Traverse the goods in positive order （ Numbers ）  Traversal in reverse order consists of and （ Backpack Capacity ）
        for i in range(len(stones)):
            for j in range(target, stones[i]-1, -1):
                dp[j] = max(dp[j], dp[j-stones[i]] + stones[i])
        
        #  The rest of the heap is total - dp[target]  Subtracting the   Is the value 
        return (total - dp[target]) - dp[target]