数学建模——整数规划

目录

基本概念

整数规划模型求解

整数线性规划模型求解

蒙特卡洛求解 

遗传算法求解 

 其他

---

基本概念

一部分或全部决策变量必须取整数值的规划问题称为整数规划。

纯整数规划：全部决策变量都为整数；混合整数规划：决策变量有一部分是整数值，另一部分不是整数；0-1整数规划：决策变量只能取0或1的整数规划。

整数线性规划模型（一个线性规划模型中的部分或全部决策变量为整数）一般形式：

有时，也可以通过引入0-1变量将一些特定的非线性约束条件进行线性化。如果有m个相互排斥的约束条件，即同一时间只能有一个条件起作用，则引入m个0-1变量：

和一个充分大的正常数M，则下面这一组m+1个约束条件就合于上述要求：

整数规划模型求解

整数线性规划模型求解

例如求解如下整数规划：

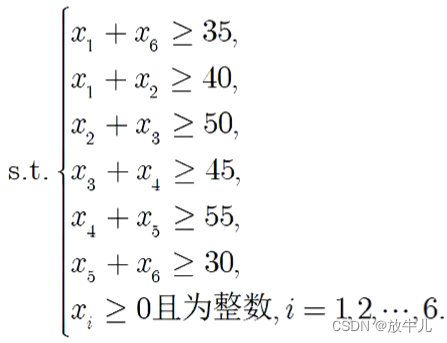
clc,clear
prob = optimproblem;
x = optimvar('x',6,'Type','integer','LowerBound',0);
prob.Objective = sum(x);
con = optimconstr(6); %创建空优化约束数组
a = [35,40,50,45,55,30];
con(1) = x(1)+x(6) >= 35;
for i = 1:5
    con(i+1) = x(i)+x(i+1) >= a(i+1);
end
prob.Constraints.con = con;
[sol,fval,flag] = solve(prob);
sol.x,fval

ans =

    35
     5
    45
     0
    55
     0
fval =

   140

 也能这样编：

蒙特卡洛求解 

蒙特卡洛法也称为计算机模拟法，类似于在一个已知面积的正方形区域内，求其包围的不规则图形的面积，撒数目很大的豆子，根据豆子的数目比例，求得面积。

unifrnd(A,B)%生成被A和B指定上下端点[A,B]的连续均匀分布的随机数组R。

R = unifrnd(A,B,m,n,...)

R = unifrnd(A,B,[m,n,...])%返回m*n*...数组

rng(1)%1作为随机数种子，为了进行一致性的比较。

rng('shuffle')%根据当前时间为随机数生成器提供种子。

tic%计时开始

toc%计时结束

B = all(A)%如果A是二维的，列数为n，则B为一个1*n的矩阵。如果A中某一列的元素全为真，则B中对应元素为1。如果A是三维的，则B的列数、页数和A相同，B的行数为1。高于三维的情况可以以此类推。

例如求解非线性整数规划：x均为整数

clc,clear
rng(0);
p0 = 0;
n = 10^6;
tic;
for i = 1:n
    x = randi([0,99],1,5);
    [f,g] = mente(x);
    if all(g <= 0)
        if p0 <f
            x0 = x;p0 = f;
        end
    end
end
x0,p0,toc

function [f,g] = mente(x)
f = x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)^2-8*x(1)-2*x(2)...
    -3*x(3)-x(4)-2*x(5);
g = [sum(x)-400
    x(1)+2*x(2)+2*x(3)+x(4)+6*x(5)-800
    2*x(1)+x(2)+6*x(3)-200
    x(3)+x(4)+5*x(5)-200];
end

x0 =

    46    98     1    99     3
p0 =

       50273

历时 0.927967 秒。

遗传算法求解 

 fun是目标函数（只能最小值），nvars表示变量个数，A、b线性不等号约束，Aeq、beq线性等号约束，lb、ub表示上下界，nonlcon表示非线性约束，intcon指明哪些变量是整数变量，options用来指明其他一些优化设置。

还采用上面那个例子：

clc,clear
f = @(x) x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)^2-8*x(1)-2*x(2)...
    -3*x(3)-x(4)-2*x(5);
A = [1,1,1,1,1;
    1,2,2,1,6;
    2,1,6,0,0;
    0,0,1,1,5];
b = [400;800;200;200];
[x,fvdisc] = ga(@(x)-f(x),5,A,b,[],[],zeros(1,5),99*ones(1,5),[],[1:5])

 @(x)-f(x)表示又定义一个匿名函数是-f(x)

x =

    50    99     0    99    20
fvdisc =

      -51568 

 其他

解决实际问题经过：问题分析、模型假设、符号说明、模型建立。

MATLAB中一行太长可以使用"..."来换行