当前位置:网站首页>【ACWing】909. 下棋游戏
【ACWing】909. 下棋游戏
2022-07-24 15:24:00 【记录算法题解】
题目地址:
https://www.acwing.com/problem/content/911/
给定一个有向无环图作为棋盘,棋盘上有 M M M个棋子,多个棋子可以放到棋盘中的同一个点上。两名玩家在棋盘上进行游戏,每名玩家每回合需要移动任意一个棋子沿着一条有向边移动至与它相邻的任意一个点上。当轮到一名玩家时,该玩家如果无法移动任何棋子,则视为游戏失败。请问先手是否必胜。
输入格式:
第一行包含整数 N N N,表示图中共有 N N N个点。
接下来 N N N行,每行包含若干个整数,第一个整数 X i X_i Xi表示从编号为 i i i的点出发的有向边的条数,接下来 X i X_i Xi个数字表示每条有向边的终点。
点的编号为 0 0 0到 N − 1 N−1 N−1,上述 N N N行数据按顺序依次介绍由 0 ∼ N − 1 0∼N−1 0∼N−1号点出发的有向边的条数和每条边的终点。
再接下来若干行是询问,每行首先包含一个整数 M M M,表示一组询问中的棋子个数,接下来包含 M M M个整数,表示 M M M个棋子所在的初始点的编号。
最后一行为一个整数 0 0 0,表示输入结束。
输出格式:
每组询问输出一个结果,每个结果占一行,如果先手必胜则输出WIN,否则输出LOSE。
数据范围:
1 ≤ N ≤ 10000 1≤N≤10000 1≤N≤10000
1 ≤ M ≤ 10 1≤M≤10 1≤M≤10
数据保证图中边的数量不会超过 1 0 5 10^5 105条。
询问次数不会超过 10000 10000 10000次。
可以用SG函数做。参考https://blog.csdn.net/qq_46105170/article/details/114006814。对于本题的有向图,可以先求出每个点的SG函数值,由于棋子之间互相独立,可以看成是 M M M个独立的游戏在同时进行,那么由SG定理,只需要把所有棋子的初始位置的SG函数做一下异或,如果非零,则先手必胜,否则先手必败。代码如下:
#include <iostream>
#include <cstring>
#include <unordered_set>
using namespace std;
const int N = 10010, M = N * 10;
int n, m;
int h[N], e[M], ne[M], idx;
int f[N];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int sg(int x) {
if (~f[x]) return f[x];
unordered_set<int> st;
for (int i = h[x]; ~i; i = ne[i])
st.insert(sg(e[i]));
for (int i = 0;; i++)
if (!st.count(i))
return f[x] = i;
}
int main() {
memset(h, -1, sizeof h);
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &m);
while (m--) {
int x;
scanf("%d", &x);
add(i, x);
}
}
memset(f, -1, sizeof f);
while (cin >> m, m) {
int res = 0;
while (m--) {
int x;
scanf("%d", &x);
res ^= sg(x);
}
res ? puts("WIN") : puts("LOSE");
}
}
预处理时间复杂度 O ( N M ) O(NM) O(NM)(可以将算SG函数的时间都算作是预处理),每次询问时间复杂度 O ( M ) O(M) O(M),空间 O ( N M ) O(NM) O(NM)。
边栏推荐
- 野火stm32霸道,通过固件库实现流水灯
- Performance test - Test Execution
- MongoDB入门学习
- You can't just focus on flex layout and elaborate animation to explain all flex layout methods! Easy to understand dry goods tutorial
- Android SQLite database practice
- 24.原生磁盘的使用
- 2022 RoboCom 世界机器人开发者大赛-本科组(省赛)-- 第五题 树与二分图 (已完结)
- 被攻击怎么解决?DDoS高防IP防护策略
- Use of keywords const, volatile and pointer; Assembly language and view of register status
- Is it safe for Huatai Securities to open an account? I don't know how to operate it
猜你喜欢

26. Code implementation of file using disk

MySQL build master-slave synchronization - build with docker
【TA-霜狼_may-《百人计划》】图形3.4 延迟渲染管线介绍
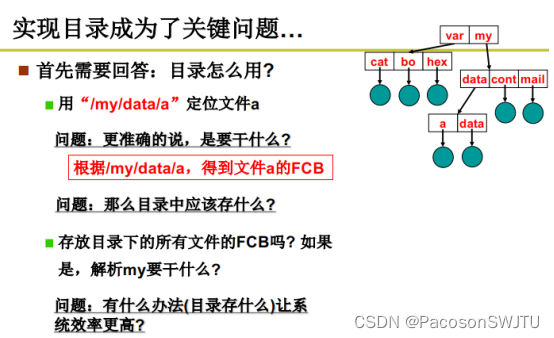
27.目录与文件系统
Kubectl_好用的命令行工具:oh-my-zsh_技巧和窍门

2022 robocom world robot developer competition - undergraduate group (provincial competition) rc-u4 strategy team (completed)

Intuitive understanding of various normalization
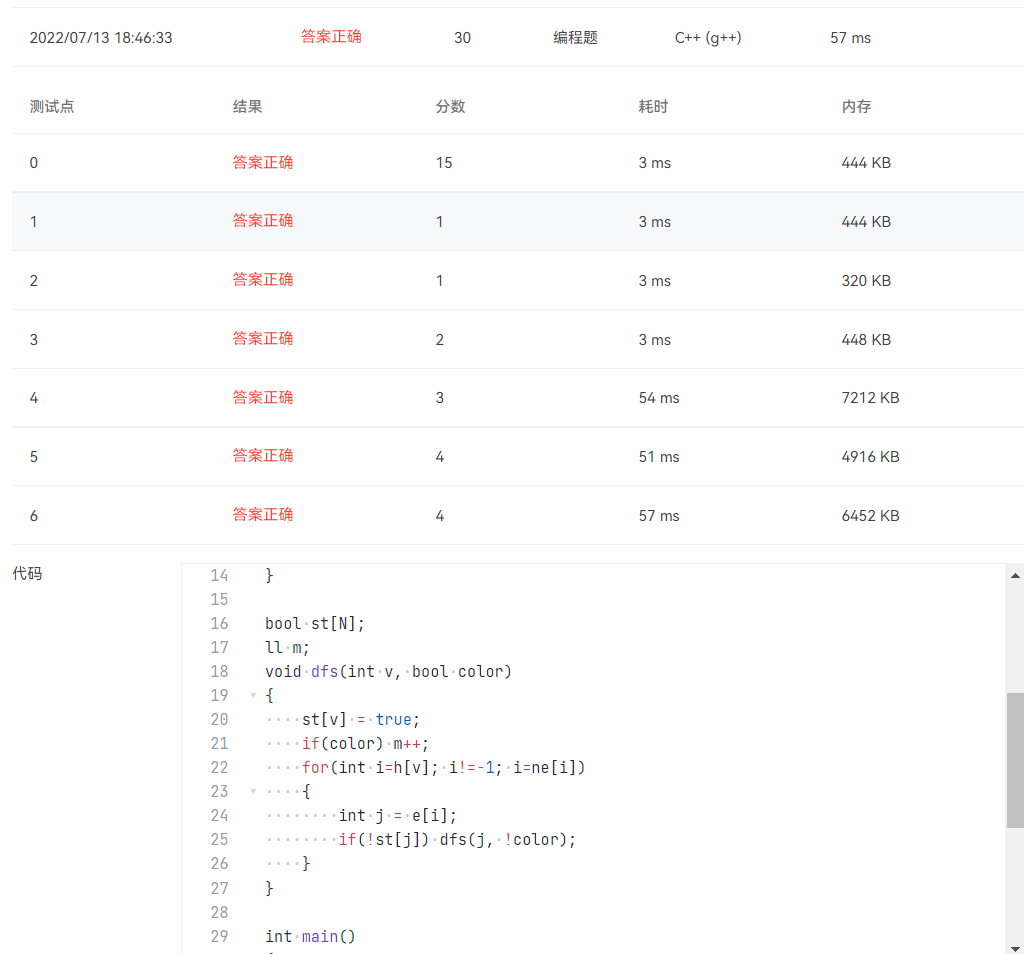
2022 robocom world robot developer competition - undergraduate group (provincial competition) -- fifth question tree and bipartite diagram (completed)

Simple encapsulation of wechat applet wx.request

Huawei wireless device configuration wpa2-802.1x-aes security policy
随机推荐
Cloud development standalone image Jiugongge traffic main source code
Performance test - Preparation of test plan
Simple encapsulation of wechat applet wx.request
遭受DDoS时,高防IP和高防CDN的选择
[300 opencv routines] 238. Harris corner detection in opencv
(零九)Flask有手就行——Cookie和Session
云开发单机版图片九宫格流量主源码
DS inner row heap sort
Intelligent operation and maintenance scenario analysis: how to detect abnormal business system status through exception detection
Intuitive understanding of various normalization
AG. DS binary tree -- hierarchical traversal
Outlook tutorial, how to create tasks and to DOS in outlook?
Leetcode 1288. delete the covered interval (yes, solved)
基于Lambert函数的时滞系统稳定性研究
You can't just focus on flex layout and elaborate animation to explain all flex layout methods! Easy to understand dry goods tutorial
C - partial keyword
Wildfire STM32 domineering, through the firmware library to achieve water light
Force button 31. Next arrangement -- double finger needling
Kubectl_ Easy to use command line tool: Oh my Zsh_ Tips and tricks
Existence form and legitimacy of real data in C language (floating point number)