当前位置:网站首页>[combinatorics] generating function (use generating function to solve the combination number of multiple sets R)
[combinatorics] generating function (use generating function to solve the combination number of multiple sets R)
2022-07-03 18:00:00 【Programmer community】
List of articles
- One 、 Use the generating function to solve multiple sets r Combinatorial number
- Two 、 Use the generating function to solve multiple sets r Combinatorial number Example
Reference blog :
- 【 Combinatorial mathematics 】 Generating function Brief introduction ( Generating function definition | Newton's binomial coefficient | Common generating functions | Related to constants | Related to binomial coefficient | Related to polynomial coefficients )
- 【 Combinatorial mathematics 】 Generating function ( Linear properties | Product properties )
- 【 Combinatorial mathematics 】 Generating function ( Shift property )
- 【 Combinatorial mathematics 】 Generating function ( The nature of summation )
- 【 Combinatorial mathematics 】 Generating function ( Commutative properties | Derivative property | Integral properties )
- 【 Combinatorial mathematics 】 Generating function ( Summary of nature | Important generating functions ) *
- 【 Combinatorial mathematics 】 Generating function ( Generate function examples | Given the general term formula, find the generating function | Given the generating function, find the general term formula )
- 【 Combinatorial mathematics 】 Generating function ( Generate function application scenarios | Solving recursive equations using generating functions )
One 、 Use the generating function to solve multiple sets r Combinatorial number
S
=
{
n
1
⋅
a
1
,
n
2
⋅
a
2
,
⋯
,
n
k
⋅
a
k
}
S = \{ n_1 \cdot a_1, n_2 \cdot a_2, \cdots, n_k \cdot a_k \}
S={ n1⋅a1,n2⋅a2,⋯,nk⋅ak} Is a multiple set , It contains
k
k
k Elements of kinds ,
n
1
,
n
2
,
⋯
,
n
k
n_1, n_2, \cdots, n_k
n1,n2,⋯,nk Is the repetition of each element ,
The Of multiple sets
r
r
r Combinatorial number , yes Indefinite equation
x
1
+
x
2
+
⋯
+
x
k
=
r
x_1 + x_2 + \cdots + x_k = r
x1+x2+⋯+xk=r Nonnegative integer solution of , Premise is
x
i
≤
n
i
x_i \leq n_i
xi≤ni , The number of each element
x
i
x_i
xi , Cannot exceed its repeatability
n
i
n_i
ni ;
amount to
a
1
a_1
a1 take
x
1
x_1
x1 individual ,
a
2
a_2
a2 take
x
2
x_2
x2 individual ,
⋯
\cdots
⋯ ,
a
k
a_k
ak take
x
k
x_k
xk individual , Total
r
r
r individual ;
n
i
n_i
ni Is an infinite number , Of multiple sets
r
r
r The number of combinations is
C
(
k
+
r
−
1
,
r
)
C(k + r - 1, r)
C(k+r−1,r)
Review multiple set permutations :
- Repeatable elements , Orderly selection , Corresponding Arrangement of multiple sets ;
whole
row
Column
=
n
!
n
1
!
n
2
!
⋯
n
k
!
Full Permutation = \cfrac{n!}{n_1! n_2! \cdots n_k!}
whole row Column =n1!n2!⋯nk!n! , Incomplete permutation
k
r
,
r
≤
n
i
k^r , \ \ r\leq n_i
kr, r≤ni
- Repeatable elements , Unordered selection , Corresponding Combination of multiple sets ;
N
=
C
(
k
+
r
−
1
,
r
)
N= C(k + r - 1, r)
N=C(k+r−1,r)
Aforementioned Multiple sets
r
r
r Combinatorial number
C
(
k
+
r
−
1
,
r
)
C(k + r - 1, r)
C(k+r−1,r) It is the selection result under the condition of unlimited repetition , If Repeatability is limited , You need to use the generating function to calculate ;
Add the following restrictions :
a
1
a_1
a1 At most
3
3
3 individual ,
a
2
a_2
a2 Take the least
4
4
4 individual , Most take
10
10
10 individual ;
Generating function :
G
(
y
)
=
G(y) =
G(y)=
(
1
+
y
+
⋯
+
y
n
1
)
(1 + y + \cdots + y^{n_1})
(1+y+⋯+yn1)
(
1
+
y
+
⋯
+
y
n
2
)
(1 + y + \cdots + y^{n_2})
(1+y+⋯+yn2)
⋯
\cdots
⋯
(
1
+
y
+
⋯
+
y
n
k
)
(1 + y + \cdots + y^{n_k})
(1+y+⋯+ynk)
The number of values of each element in the multiset is taken as
y
y
y Power of power , Such as
a
1
a_1
a1 The number of values of elements is
0
0
0 To
n
1
n_1
n1 , Then the corresponding The generated function item is from
y
y
y Of
0
0
0 The next power , To
y
y
y Of
n
1
n_1
n1 The next power Add up ; Constituent items
(
1
+
y
+
⋯
+
y
n
1
)
(1 + y + \cdots + y^{n_1})
(1+y+⋯+yn1) ;
Put all the elements above Generate function items Ride together , It constitutes the above generating function ;
Multiply by polynomials , Multiple centralized fetches
r
r
r Elements ,
From the first factor
(
1
+
y
+
⋯
+
y
n
1
)
(1 + y + \cdots + y^{n_1})
(1+y+⋯+yn1) take out
y
x
1
y^{x_1}
yx1 ,
From the second factor
(
1
+
y
+
⋯
+
y
n
2
)
(1 + y + \cdots + y^{n_2})
(1+y+⋯+yn2) take out
y
x
2
y^{x_2}
yx2 ,
⋮
\vdots
⋮
From
k
k
k Personal factor
(
1
+
y
+
⋯
+
y
n
k
)
(1 + y + \cdots + y^{n_k})
(1+y+⋯+ynk) take out
y
x
k
y^{x_k}
yxk ,
If the above product
y
x
1
y
x
2
⋯
y
x
k
y^{x_1}y^{x_2}\cdots y^{x_k}
yx1yx2⋯yxk Result yes
y
r
y^{r}
yr , namely
y
x
1
y
x
2
⋯
y
x
k
=
y
r
y^{x_1}y^{x_2}\cdots y^{x_k} = y^{r}
yx1yx2⋯yxk=yr , Equivalent to index
x
1
+
x
2
+
⋯
+
x
k
=
r
x_1 + x_2 + \cdots + x_k = r
x1+x2+⋯+xk=r , That is, the nonnegative integer solution of the indefinite equation ;
Two 、 Use the generating function to solve multiple sets r Combinatorial number Example
Multiple sets
S
=
{
3
⋅
a
,
4
⋅
b
,
5
⋅
c
}
S = \{3\cdot a , 4 \cdot b , 5 \cdot c \}
S={ 3⋅a,4⋅b,5⋅c} , Find the
10
10
10 Combinatorial number ;
Of the above multiset elements Repeatability
3
,
4
,
5
3,4,5
3,4,5 Not more than
10
10
10 ;
Corresponding
a
a
a Elements , Its The value range of repeatability is
0
0
0 ~
3
3
3 , The corresponding generating function item is
y
0
+
y
1
+
y
2
+
y
3
y^0 +y^1 + y^2 + y^3
y0+y1+y2+y3
Corresponding
b
b
b Elements , Its The value range of repeatability is
0
0
0 ~
4
4
4 , The corresponding generating function item is
y
0
+
y
1
+
y
2
+
y
3
+
y
4
y^0 +y^1 + y^2 + y^3 + y^4
y0+y1+y2+y3+y4
Corresponding
c
c
c Elements , Its weight The range of complexity is
0
0
0 ~
5
5
5 , The corresponding generating function item is
y
0
+
y
1
+
y
2
+
y
3
+
y
4
+
y
5
y^0 +y^1 + y^2 + y^3 + y^4 + y^5
y0+y1+y2+y3+y4+y5
Multiply the above items , Get the complete generating function ;
G
(
x
)
=
(
y
0
+
y
1
+
y
2
+
y
3
)
(
y
0
+
y
1
+
y
2
+
y
3
+
y
4
)
(
y
0
+
y
1
+
y
2
+
y
3
+
y
4
+
y
5
)
G(x) = (y^0 +y^1 + y^2 + y^3)(y^0 +y^1 + y^2 + y^3 + y^4)(y^0 +y^1 + y^2 + y^3 + y^4 + y^5)
G(x)=(y0+y1+y2+y3)(y0+y1+y2+y3+y4)(y0+y1+y2+y3+y4+y5)
=
(
1
+
y
1
+
y
2
+
y
3
)
(
1
+
y
1
+
y
2
+
y
3
+
y
4
)
(
1
+
y
1
+
y
2
+
y
3
+
y
4
+
y
5
)
\ \ \ \ \ \ \ \ \ \ =(1 +y^1 + y^2 + y^3)(1 +y^1 + y^2 + y^3 + y^4)(1 +y^1 + y^2 + y^3 + y^4 + y^5)
=(1+y1+y2+y3)(1+y1+y2+y3+y4)(1+y1+y2+y3+y4+y5)
=
(
1
+
2
y
1
+
3
y
2
+
4
y
3
+
4
y
4
+
3
y
5
+
2
y
6
+
y
7
)
(
1
+
y
1
+
y
2
+
y
3
+
y
4
+
y
5
)
\ \ \ \ \ \ \ \ \ \ =(1 +2y^1 + 3y^2 + 4y^3 + 4y^4 + 3y^5 + 2y^6 + y^7 )(1 +y^1 + y^2 + y^3 + y^4 + y^5)
=(1+2y1+3y2+4y3+4y4+3y5+2y6+y7)(1+y1+y2+y3+y4+y5)
Multiply the above two items ,
y
y
y The power of is
10
10
10 The item :
The first factor
3
y
5
3y^5
3y5 With the second factor
y
5
y^5
y5 , Multiply by
3
y
10
3y^{10}
3y10
The first factor
2
y
6
2y^6
2y6 With the second factor
y
4
y^4
y4 , Multiply by
2
y
10
2y^{10}
2y10
The first factor
y
7
y^7
y7 With the second factor
y
3
y^3
y3 , Multiply by
y
10
y^{10}
y10
y
10
y^{10}
y10 The coefficient before the term is
3
+
2
+
1
=
6
3 + 2+1 = 6
3+2+1=6
So the above Of multiple sets
10
10
10 Combine , The options are
6
6
6 Kind of ;
边栏推荐
- Servlet specification Part II
- Brief introduction to the core functions of automatic penetration testing tool
- SDNUOJ1015
- A. Odd Selection【BruteForce】
- STM32 realizes 74HC595 control
- Distributed task distribution framework gearman
- [combinatorics] generating function (commutative property | derivative property | integral property)
- Lesson 13 of the Blue Bridge Cup -- tree array and line segment tree [exercise]
- Leetcode 538 converts binary search tree into cumulative tree -- recursive method and iterative method
- PHP MySQL where clause
猜你喜欢
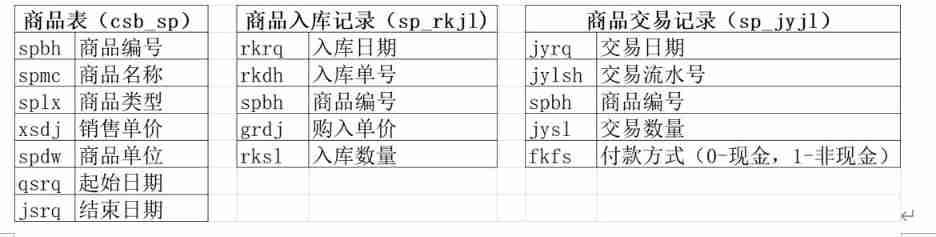
Five problems of database operation in commodity supermarket system

Getting started with deops

Tensorboard quick start (pytoch uses tensorboard)

1147_ Makefile learning_ Target files and dependent files in makefile

Leetcode Valentine's Day Special - looking for a single dog

Analysis report on production and marketing demand and investment forecast of China's PVC industry from 2021 to 2026
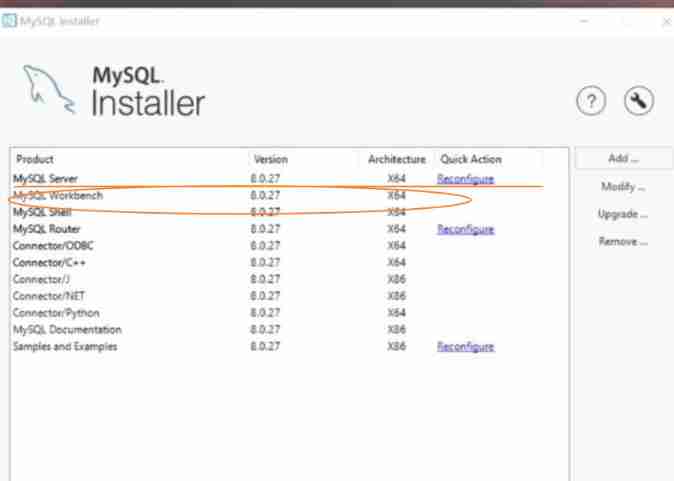
MySQL has been stopped in the configuration interface during installation
![[set theory] order relation: summary (partial order relation | partial order set | comparable | strictly less than | covering | hasto | total order relation | quasi order relation | partial order rela](/img/df/a034032e203e7935dafaf8a71cb6c8.jpg)
[set theory] order relation: summary (partial order relation | partial order set | comparable | strictly less than | covering | hasto | total order relation | quasi order relation | partial order rela
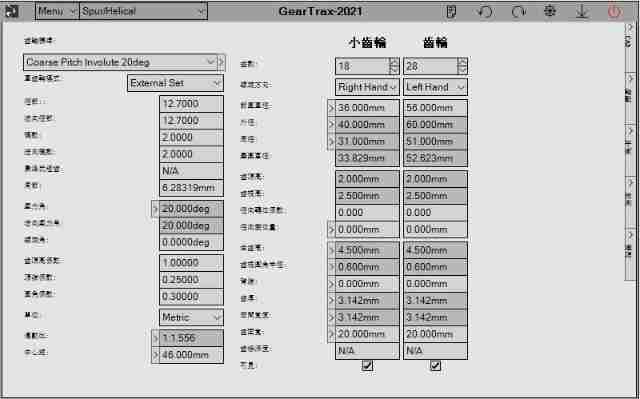
Introduction to SolidWorks gear design software tool geartrax

STM32实现74HC595控制
随机推荐
聊聊支付流程的设计与实现逻辑
Research Report on market demand and investment planning for the development of China's office chair industry, 2022-2028
PHP MySQL create database
Leetcode 669 pruning binary search tree -- recursive method and iterative method
Ml (machine learning) softmax function to realize the classification of simple movie categories
Discussion sur la logique de conception et de mise en oeuvre du processus de paiement
Line by line explanation of yolox source code of anchor free series network (5) -- mosaic data enhancement and mathematical understanding
MySQL grouping query
Market demand survey and marketing strategy analysis report of global and Chinese pet milk substitutes 2022-2028
Three gradient descent methods and code implementation
How to deploy applications on kubernetes cluster
win32:堆破壞的dump文件分析
Assembly for unloading Loadfrom() loaded assembly - unloading the assembly loaded with assembly LoadFrom()
远程办公工具分享|社区征文
The gbase 8A database does not support the DB2 function value (column_name, 0) cluster syntax
[Yu Yue education] family education SPOC class 2 reference materials of Shanghai Normal University
Analysis report on production and marketing demand and investment forecast of China's PVC industry from 2021 to 2026
PHP MySQL inserts data
AcWing 271. 杨老师的照相排列【多维DP】
圖像24比特深度轉8比特深度