当前位置:网站首页>[image processing] spatial domain image enhancement
[image processing] spatial domain image enhancement
2022-06-11 09:01:00 【Jeff_ zvz】

Catalogue
Spatial domain image enhancement
Introduction
The spatial domain is divided into separate pixel processing and neighborhood processing . Pixel processing one pixel at a time , And only focus on this pixel and have nothing to do with the neighborhood , Neighborhood processing is generally filtering convolution , The essence is convolution of image and mask .
Pixel processing
Pixel processing is mapping : Z = T ( r ) \Zeta = \Tau(r) Z=T(r)
Gray scale transformation
Identity transformation
Z = r \Zeta = r Z=r
Reverse transformation
Z = L − r \Zeta = L - r Z=L−r
def inverse_transform(img):
p_max = np.max(np.max(img))
out = p_max - img
return out
Logarithmic transformation
Z = c ∗ log 2 r + 1 \Zeta = c*\log_{2}^{r+1} Z=c∗log2r+1
or
Z = c ∗ log v + 1 1 + v ∗ r \Zeta = c*\log_{v+1}^{1+v*r} Z=c∗logv+11+v∗r
Logarithmic transformation can expand the low gray value part of the image , Show more details in the low gray part , Compress its high gray value part , Reduce the details of high gray value parts , So as to emphasize the low gray part of the image .
Logarithmic transformation realizes the effect of expanding low gray value and compressing high gray value , It is widely used in the display of spectrum images . The typical application of logarithmic transformation is the wide dynamic range of Fourier spectrum , During direct display, a large number of dark details are lost due to the limitation of the dynamic range of the display device ; The dynamic range of the image is nonlinearly compressed by logarithmic transform , You can clearly show .
def image_log(img):
img_c = img/255.
return np.uint8(np.log(1+img_c) *255)
def img_log(v,img):
img_c = img/255.
return np.uint8(np.log(1+v*img_c)/np.log(v+1) * 255)
Power law transformation ( Gamma transform )
Z = c ∗ ( r + a ) γ \Zeta = c*(r+a)^γ Z=c∗(r+a)γ
Gamma transform is essentially a power operation on each value in the image matrix .0< γ<1 when , Stretch the area with low gray level in the image , Compress parts with higher gray levels , Increase the contrast of the image ;γ > 1 when , Stretch the area with higher gray level in the image , Compress parts with lower gray levels , Reduce the contrast of the image .
Gamma transform compensates human visual characteristics through nonlinear transformation , Maximize the use of effective gray level bandwidth . A lot of shooting 、 Show 、 The brightness curve of the printing device conforms to the power-law curve , Therefore, gamma transform is widely used in the adjustment of display effects of various devices , Called gamma correction .

def gamma_transform(img,gamma=2,eps=0):
return 255*(((img+eps)/255.)**gamma)
Piecewise transformation
Use a mask to segment , And then process in sections .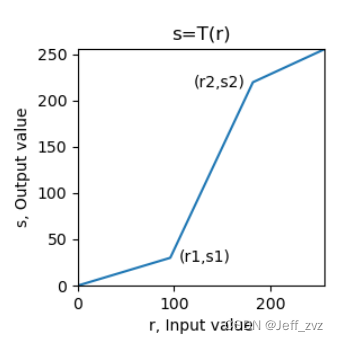
def fenduan(img,x1,x2,y1,y2):
if x1==x2 or x2==255:
return None
# Mask
m1 = (img<x1)
m2 = (img>=x1)& (img <= x2)
m3 = (img>x2)
out = (img*y1/x1)*m1 + (((img-x1)*(y2-y1)/(x2-x1))+y1)*m2 \
+(((255-y2)*(img-x2)/(255-x2))+y2)*m3
return out
You can also use gray levels for layering
imgLayer1[(imgLayer1[:,:]<a) | (imgLayer1[:,:]>b)] = 0 # Other areas : black
imgLayer1[(imgLayer1[:,:]>=a) & (imgLayer1[:,:]<=b)] = 255 # Grayscale window : white
Threshold transformation
Z = { z 1 , x ≤ t h 1 z 2 , x > t h 2 (1) \Zeta= \begin{cases} z1,\quad x\leq th1\\ z2, \quad x>th2 \end{cases} \tag{1} Z={ z1,x≤th1z2,x>th2(1)
Below a threshold , become z1; Above a certain threshold , become z2.cv2.threshold(src,thresh,maxval,type[,dst])->retval, dst
- scr: The input image of the transform operation ,nparray Two dimensional array , Must be a single channel grayscale image !
- thresh: threshold , Value range 0~255
- maxval: Fill color , Value range 0~255, Usually take 255
- type: Transformation type
cv2.THRESH_BINARY: Set when greater than the threshold 255, Otherwise, set 0
cv2.THRESH_BINARY_INV: Set when greater than the threshold 0, Otherwise, set 255
cv2.THRESH_TRUNC: When it is greater than the threshold value, it is set as the threshold value thresh, Otherwise unchanged ( Keep the primary color )
cv2.THRESH_TOZERO: It does not change when it is greater than the threshold ( Keep the primary color ), Otherwise, set 0
cv2.THRESH_TOZERO_INV: Set when greater than the threshold 0, Otherwise unchanged ( Keep the primary color )
cv2.THRESH_OTSU: Use OTSU Algorithm selection threshold- Return value retval: Returns the threshold of binarization
- Return value dst: Returns the output image of the threshold transformation
Histogram Processing
Histogram
A histogram is a graph showing the number of grayscale levels .
Normalized histogram normalizes it , Show its probability distribution .
def hist(img_c):
r,c = img_c.shape
img_c = img_c.flatten() # Flattening
img_c = img_c.tolist()
myhist = [img_c.count(i)/(r*c) for i in range(256)] # normalization
return myhist
opencv Middle function cv2.calcHist(images, channels, mask, histSize, ranges[, hist[, accumulate ]]) → hist
images: The input image , use [] Brackets indicate
channels: Histogram calculation channel , use [] Brackets indicate , The grayscale is 0
mask: mask image , It's usually set to None
histSize: Number of square columns , Usually take 256
ranges: Value range of pixel value , It's usually [0,256]
Return value hist: Returns the total number of pixels in the image for each pixel value , Shape is (histSize,1)
Histogram equalization
Histogram equalization is to change the irregular gray distribution into a regular and balanced gray distribution . The basic idea of histogram equalization is to widen the gray level which accounts for a large proportion in the image , The gray level with small proportion is compressed , Make the histogram distribution of the image more uniform , Expand the dynamic range of gray value difference , So as to enhance the overall contrast of the image .
There are conclusions in probability theory :
When there is Z = T (\r) when , There is a probability distribution :
P z ( z ) = P r ( r ) ∗ ∣ d z ∣ / ∣ d r ∣ P_z(z) = P_r(r) * |dz|/|dr| Pz(z)=Pr(r)∗∣dz∣/∣dr∣
And easy to prove
T ( r ) = ( L − 1 ) ∗ ∫ 0 r P w ( w ) d w T(r) = (L-1) * \int_0^r P_w(w)dw T(r)=(L−1)∗∫0rPw(w)dw
Discrete form
From the above T(\r), And the image is discrete , Transform function T(\r) Is the accumulation of probability distributions , A curve is similar to a trapezoid monotonically increasing .
def get_pdf(img): # Probability density distribution
total = img.shape[0]*img.shape[1]
return [np.sum(img==i)/total for i in range(256)]
def hist_equal(img):
pdf = get_pdf(img)
out = np.copy(img)
s = 0.
Tr = [] # Transform function
for i in range(256):
s = s+pdf[i]
out[(img==i)] = s*255.
Tr.append(s*255.)
out = out.astype(np.uint8)
return out,Tr
opencv function cv2.equalizeHist(src[, dst]) → dst
Histogram matching ( Histogram normalization )
Suppose the graph 2 The histogram effect is the histogram we want , Our original picture is 1. It is known that we can histogram equalize the graph 1、 chart 2 All become over histogram , From the transformation function we can get the graph 2 Mapping table to transition histogram , So we can inverse map back to graph 2.

def get_pdf(img): # Probability density distribution
total = img.shape[0]*img.shape[1]
return [np.sum(img==i)/total for i in range(256)]
def hist_equal(img):
pdf = get_pdf(img)
out = np.copy(img)
s = 0.
Tr = [] # Transform function
for i in range(256):
s = s+pdf[i]
out[(img==i)] = s*255.
Tr.append(s*255.)
out = out.astype(np.uint8)
return out,Tr
def gen_eq_pdf(): # Generate uniform distribution , The histogram we want
return [0.0039 for i in range(256)] # 1/256 = 0.0039
def gen_target_table(Pv): #Pv To build a good probability distribution histogram
table = []
# The following code is to execute G Transformation , equalization ( The vertical axis ) Map to ideal histogram ( The horizontal axis )
SUMq = 0.
for i in range(256): # Known grayscale values are from 0 To 255, By transforming functions , Map to vertical axis , Form mapping table
SUMq = SUMq + Pv[i]
table.append(np.round(SUMq*255,0)) # rounding
return table
def hist_specify(img):
Pv = gen_eq_pdf()
table = gen_target_table(Pv)
ori_img,T_trans = hist_equal(img) #ori_img Namely B'
out = ori_img.copy() # Construct output image
map_val = 0 # The inverse mapping value is initialized to 0
for v in range(256):
if v in ori_img:
if v in table:
map_val = len(table)-table[::-1].index(v)-1 # find , Take the largest one
out[(ori_img == v)] = map_val # No inverse mapping relationship found , Take the previous one
return out
Local histogram equalization
Histogram equalization and histogram matching are based on the global transformation of the gray distribution of the whole image , It is not for the details of the local area of the image .
Histogram processing is also applicable to local , The idea of local histogram processing is to transform the histogram based on the gray distribution of the pixel neighborhood .
The process :
(1) Set a template of a certain size ( Rectangular neighborhood ), Move pixel by pixel in the image ;
(2) For each pixel position , Calculate the histogram of the template area , Histogram equalization or histogram matching transformation is performed on the local region , The transformation result is only used for the gray value correction of the central pixel of the template area ;
(3) Templates ( Neighborhood ) Move line by line and column by column in the image , Traverse all pixels , Complete the local histogram processing of the whole image .
opencv function :cv2.createCLAHE([, clipLimit[, tileGridSize]]) → retval
- clipLimit: Threshold of color contrast , optional , The default value is 8
- titleGridSize: Template for local histogram equalization ( Neighborhood ) size , optional , The default value is (8,8)
cv2. createCLAHE It is an adaptive histogram equalization method with limited contrast (Contrast Limited Adaptive Hitogram Equalization), The method of limiting histogram distribution and accelerated interpolation are adopted .
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('img/low_pix.jpg',0)
imgequ = cv2.equalizeHist(img)
clahe = cv2.createCLAHE(clipLimit=2.0,tileGridSize=(4,4))
imglocalequ = clahe.apply(img)
plt.figure(figsize=(9, 6))
plt.subplot(131), plt.title('Original'), plt.axis('off')
plt.imshow(img, cmap='gray', vmin=0, vmax=255)
plt.subplot(132), plt.title(f'Global Equalize Hist'), plt.axis('off')
plt.imshow(imgequ, cmap='gray', vmin=0, vmax=255)
plt.subplot(133), plt.title(f'Local Equalize Hist'), plt.axis('off')
plt.imshow(imglocalequ, cmap='gray', vmin=0, vmax=255)
plt.tight_layout()
plt.show()

Spatial filtering
Image filtering is to suppress the noise of the target image while preserving the detailed features of the image as much as possible , It is a common image preprocessing operation .
Image smoothing and filtering
Smooth filtering is also called low-pass filtering , It can suppress the gray mutation in the image , Blur the image , It's low-frequency enhanced spatial filtering technology
Mean filtering

Mean filtering is to replace the middle value with the average value of the pixel values in the neighborhood , The side effect is to blur the image ( Blur the edges ), And the larger the convolution kernel is, the more fuzzy it becomes .
Mathematically speaking , Because the mean filter will be affected by neighborhood points , The edge is an abrupt point of change , Therefore, the pixel values in this region become smooth after the mean filter convolution , The image is blurred .
The following is the mean filter after noise processing , Threshold processing .
Code :dst=cv2.blur(src ,ksize, anchor, borderType)
median filtering
Median filtering is a nonlinear smoothing technique , It is a filter based on statistical sorting method , It sorts the pixel values within the mask by one dimension , Then take the middle value as the current pixel value . Compared with the mean filter, its biggest feature is , This is an edge preserving filter , The replaced value is the original value of the image . And it can eliminate outliers , It has the best effect on salt and pepper noise .
Code :dst=cv2.medianBlur(src,ksize)
Bilateral filtering
Bilateral filtering is a compromise method that combines spatial proximity and pixel value similarity , At the same time, spatial information and gray similarity are considered , Denoising while effectively preserving the edges , It has a beautifying effect on portraits .
The edge gray changes greatly , Gaussian filtering will obviously blur the edge , Weak protection for high-frequency information . Bilateral filtering adds Gaussian variance of pixel intensity difference on the basis of Gaussian filtering , Pixels far away from the edge have little effect on the pixel value on the edge , To achieve edge protection .
Bilateral filtering can not filter high-frequency noise in color images well .
The mathematical formula is as follows :
opencv function :cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace[, dst[, borderType]]) → dst
Parameter description :
- src: The input image , It can be a grayscale image , It can also be a multi-channel color image
- dst: Output image , Size and type versus src identical
- d: The pixel neighborhood diameter of the filter kernel . Such as d<=0 , From sigmaSpace To calculate the .
- sigmaColor: Variance of filter kernel in color space , Reflect the size of the color intensity interval that produces color influence
- sigmaSpace: Variance of filter kernel in coordinate space , Reflect the size of the influence space that produces color influence
- borderType: Type of boundary extension
Guided filtering
Guided filtering is also called guided filtering , Reflect the edge through a guide picture 、 Objects and other information , Filter the input image , The content of the output image is determined by the input image , But the texture is similar to the guide picture .
The principle of guided filtering is local linear model , While maintaining the advantages of bilateral filtering ( Effectively keep edges , Non iterative computation ) At the same time, the calculation speed is very fast , So as to overcome the disadvantage of slow bilateral filtering speed .
opencv function :cv2.ximgproc_guidedFilter.filter(guide, src, d[, eps[, dDepth]) → dst
Parameter description :
- src: The input image , It can be a grayscale image , It can also be a multi-channel color image
- guide: Guide image , Size and type versus src identical
- dst: Output image , Size and type versus src identical
- d: The pixel neighborhood diameter of the filter kernel
- eps: Normalized parameters , eps The square of is similar to that in bilateral filtering sigmaColor
- dDepth: The data depth of the output picture
Image sharpening and filtering
The image is blurred by smoothing ( weighted mean ) To achieve , Similar to integral operation . Image sharpening is performed by differential operation ( Finite difference ) Realization , The change value of image gray can be obtained by first-order differentiation or second-order differentiation .
The purpose of image sharpening is to enhance the gray jump part of the image , Make the blurred image clear . Image sharpening is also called high pass filtering , Through and enhancement of high frequency , Attenuate and suppress low frequencies . Image sharpening is often used in electronic printing 、 Medical imaging and industrial testing .
- Constant gray area , The first derivative is zero , The second derivative is zero ;
- Grayscale step or ramp start area , The first derivative is nonzero ,, The second derivative is nonzero ;
- Grayscale ramp area , The first derivative is nonzero , The second derivative is zero .
Mask and derivation :
Image ,x and y Derivation of direction ( gradient ) It can be expressed by difference ( Because the image is discrete ), Both ∂ f ∂ x = f ( x + 1 , y ) − f ( x , y ) \frac{\partial f}{\partial x} = f(x+1,y) - f(x,y) ∂x∂f=f(x+1,y)−f(x,y)
The mask is
The second derivative is
∂ 2 f ∂ x 2 = f ( x − 1 , y ) + f ( x + 1 , y ) − 2 f ( x , y ) \frac{\partial ^2 f}{\partial x^2} = f(x-1,y) + f(x+1,y) - 2f(x,y) ∂x2∂2f=f(x−1,y)+f(x+1,y)−2f(x,y)
Mask as
Laplace operator
Δ f = ∂ 2 f ∂ y 2 + ∂ 2 f ∂ x 2 = f ( x − 1 , y ) + f ( x + 1 , y ) + f ( x , y − 1 ) + f ( x , y + 1 ) − 4 f ( x , y ) \Delta f= \frac{\partial ^2 f}{\partial y^2}+\frac{\partial ^2 f}{\partial x^2} = f(x-1,y) + f(x+1,y) + f(x,y-1) + f(x,y+1) - 4f(x,y) Δf=∂y2∂2f+∂x2∂2f=f(x−1,y)+f(x+1,y)+f(x,y−1)+f(x,y+1)−4f(x,y)
Mask as :

Laplace operator is a second derivative operator , The position of the edge is determined by using the quadratic differential characteristic and the zero crossing point between the peaks , More sensitive to singular points or edge points .
dst = cv2.Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]])
def Laplace(img):
edge = cv2.Laplacian(img,-1,ksize=3)
edge = cv2.convertScaleAbs(edge)
e_edge = cv2.equalizeHist(edge)
out = img + e_edge
plt.subplot(221)
plt.imshow(img,cmap='gray')
plt.title('original')
plt.subplot(222)
plt.imshow(edge,cmap='gray')
plt.title('edge')
plt.subplot(223)
plt.imshow(e_edge,cmap='gray')
plt.title('Edge enhanced')
plt.subplot(224)
plt.imshow(out,cmap='gray')
plt.title('ruihua')
plt.show()

Passivation masking
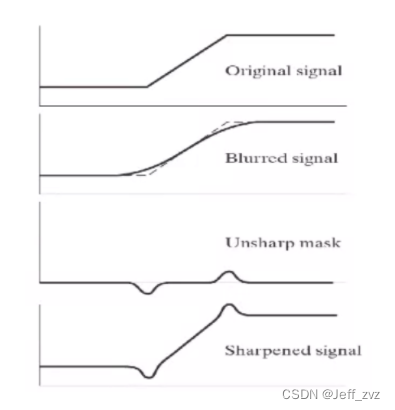
def func(img):
blur = cv2.blur(img,(5,5))
unsharp = img - blur
out = img + unsharp
plt.subplot(221)
plt.imshow(img,cmap='gray')
plt.title('original')
plt.subplot(222)
plt.imshow(blur,cmap='gray')
plt.title('blur')
plt.subplot(223)
plt.imshow(unsharp,cmap='gray')
plt.title('unsharp')
plt.subplot(224)
plt.imshow(out,cmap='gray')
plt.title('fanruihua')
plt.show()

sobel operator
Sobel Operator is a discrete differential operator , It is a joint operation of Gaussian smoothing and differential derivation , Strong anti noise ability .
Sobel Gradient operator uses local difference to find edge , Calculate the approximate value of the gradient . First calculate the level 、 Vertical gradient , Then find the total gradient . Programming implementation , The square root can be approximated by the absolute value :G = ∣ G x ∣ + ∣ G y ∣
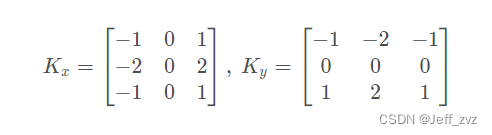
opencv function :cv2.Sobel(src, ddepth, dx, dy[, dst[, ksize[, scale[, delta[, borderType]]]]]) → dst
Parameter description :
- src: The input image , Grayscale image , Not applicable to color images
- dst: Output image , Size and type versus src identical
- ddepth: The data depth of the output picture , Select by the depth of the input image
- dx:x The order of the axial derivative ,1 or 2
- dy:y The order of the axial derivative ,1 or 2
- ksize:Sobel The size of the convolution kernel , The optional values are :1/3/5/7,ksize=-1 When using Scharr Operator operation
- scale: Scale factor , optional , The default value is 1
- delta: The offset of the output image , optional , The default value is 0
- borderType: Type of boundary extension , Note that contralateral padding is not supported (BORDER_WRAP)
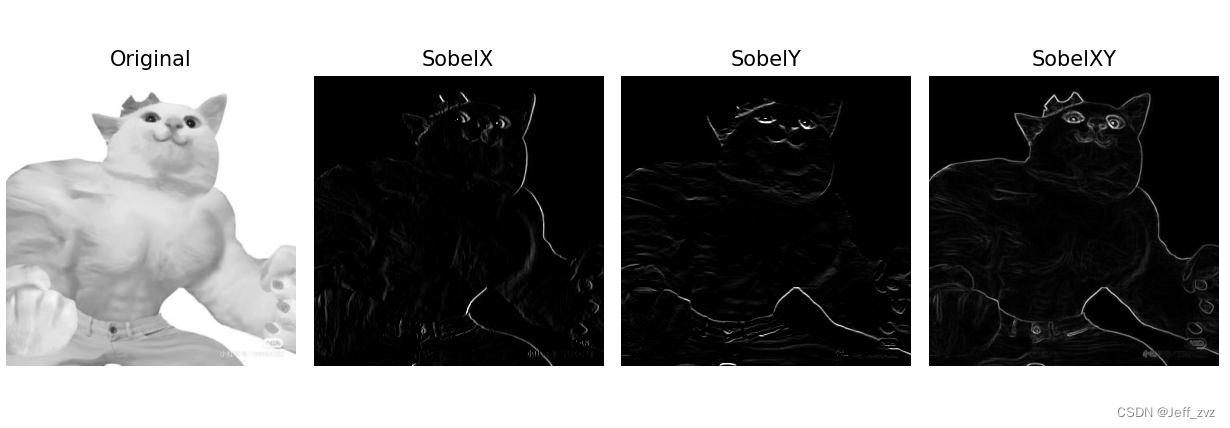
def sobel(img):
SobelX = cv2.Sobel(img, cv2.CV_16S, 1, 0) # Calculation x Axis direction
SobelY = cv2.Sobel(img, cv2.CV_16S, 0, 1) # Calculation y Axis direction
absX = cv2.convertScaleAbs(SobelX) # Turn it back uint8
absY = cv2.convertScaleAbs(SobelY) # Turn it back uint8
SobelXY = cv2.addWeighted(absX, 0.5, absY, 0.5, 0) # Approximate the square root with the absolute value
plt.figure(figsize=(10, 6))
plt.subplot(141), plt.axis('off'), plt.title("Original")
plt.imshow(img, cmap='gray', vmin=0, vmax=255)
plt.subplot(142), plt.axis('off'), plt.title("SobelX")
plt.imshow(SobelX, cmap='gray', vmin=0, vmax=255)
plt.subplot(143), plt.axis('off'), plt.title("SobelY")
plt.imshow(SobelY, cmap='gray', vmin=0, vmax=255)
plt.subplot(144), plt.axis('off'), plt.title("SobelXY")
plt.imshow(SobelXY, cmap='gray')
plt.tight_layout()
plt.show()
边栏推荐
- 682. 棒球比赛
- 领导让我重写测试代码,我也要照办嘛?
- M1 chip guide: M1, M1 pro, M1 Max and M1 ultra
- Flutter开发日志——路由管理
- leveldb简单使用样例
- Screening frog log file analyzer Chinese version installation tutorial
- openstack详解(二十四)——Neutron服务注册
- What software is required to process raw format images?
- Livedata and stateflow, which should I use?
- Erreur de démarrage MySQL "BIND on TCP / IP Port: Address already in use"
猜你喜欢

MSF evasion模块的使用

Which Apple devices support this system update? See if your old apple device supports the latest system

端口占用问题,10000端口

kubelet Error getting node 问题求助
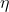
机器学习笔记 - 深度学习技巧备忘清单

How to apply for BS 476-7 sample for display? Is it the same as the display

What if the copied code format is confused?

typescript高阶特性一 —— 合并类型(&)

Matlab learning 7- linear smoothing filtering of image processing

What software is required to process raw format images?
随机推荐
2095. 删除链表的中间节点
203. remove linked list elements
Vagrant mounting pit
【C语言-指针进阶】挖掘指针更深一层的知识
Matlab learning 9- nonlinear sharpening filter for image processing
Usage and difference between map and set in JS
SAP ODATA 开发教程
MySQL核心点笔记
Matlab learning 7- linear smoothing filtering of image processing
1721. 交换链表中的节点
Screening frog log file analyzer Chinese version installation tutorial
86. separate linked list
1721. exchange nodes in the linked list
Matlab r2022a installation tutorial
19. delete the penultimate node of the linked list
Iso8191 test is mentioned in as 3744.1. Are the two tests the same?
移动端页面使用rem来做适配
机器学习笔记 - 卷积神经网络备忘清单
How to apply for BS 476-7 sample for display? Is it the same as the display
206. 反转链表


