当前位置:网站首页>Polynomial addition
Polynomial addition
2022-07-25 17:54:00 【Advanced Xiaoxin】
【 Title Description 】 Give two polynomials , Find the sum of them
【 Input 】 Give two polynomials respectively , Each polynomial gives multiple sets of inputs . Each line gives two integers a,b Express ax^b, Until input 0 0 end .( You can directly refer to the example )
【 Output 】 Write tips , After each polynomial is input, the representation of the polynomial is output immediately , After both polynomials are input , Output the sum of two polynomials .( If the description is not detailed enough, you can directly refer to the example )
【 Examples 】
Input :
8 5
-2 3
0 0
1 2
3 4
4 3
-3 3
3 0
0 0Output :
Please enter the coefficient and exponent of the first polynomial , With (0,0) end :
Please enter coefficients and exponents ( Such as :"2 3" Express 2x^3):8 5
Please enter coefficients and exponents :-2 3
Please enter coefficients and exponents :0 0
The output of the first polynomial is as follows :
8x^5-2x^3
Please enter the coefficient and exponent of the second polynomial , With (0,0) end :
Please enter coefficients and exponents ( Such as :"2 3" Express 2x^3):
1 2
Please enter coefficients and exponents :3 4
Please enter coefficients and exponents :4 3
Please enter coefficients and exponents :-3 3
Please enter coefficients and exponents :3 0
Please enter coefficients and exponents :0 0
The output of the second polynomial is as follows :
3x^4+x^3+x^2+3
8x^5+3x^4-x^3+x^2+3【 analysis 】 The problem is not difficult , Mainly because there are many pits , Think a lot . The main difficulty lies in the representation of polynomials and the addition of polynomials combine() Function writing ( The essence is the combination of linked lists ). The basic operation of linked list is the foundation , Because the exponent of a polynomial can be discontinuous and can be very large . Theoretically, it is also feasible to open a large array and sort by counting , But a big index is too space consuming , But also consider using a two-dimensional array to store coefficients , So choose to use a linked list .
The quantity of thinking focuses on the representation of polynomials , So before doing this problem , I went there first noi Of 1.13 Of the 39 topic , The title is as follows :
describe
One yuan n Polynomials of degree can be expressed as follows :
f(x)=anxn+an-1xn-1+...+a1x+a0,an≠0
among ,aixi be called i Subitem ,ai be called i Coefficient of subterm . The degree and coefficient of a univariate polynomial are given , Please output the polynomial in the format specified below :
1. The independent variable in the polynomial is x, Polynomials are given in descending order from left to right .
2. Polynomials contain only coefficients that are not 0 The item .
3. If polynomials n The coefficient of the secondary term is positive , Then the polynomial does not appear at the beginning “+” Number , If polynomials n The coefficient of the secondary term is negative , Then the polynomial is expressed in “-” At the beginning of the sign .
4. For items that are not the highest , With “+” Number or “-” No. connects this item to the previous item , It means that the coefficient is positive or negative . Followed by a positive integer , Represents the absolute value of this coefficient ( If one is higher than 0 Secondary item , The absolute value of the coefficient is 1, There is no need to output 1). If x The index of is greater than 1, Then the following exponential part is in the form of “x^b”, among b by x The index of ; If x The index of is 1, Then the following exponential part is in the form of “x”; If x The index of is 0, Then you only need to output the coefficient .
5. In polynomials , The beginning of a polynomial 、 There are no extra spaces at the end .
Input
share 2 That's ok :
first line 1 It's an integer n, Represents the degree of a univariate polynomial .
The second line has n+1 It's an integer , Among them the first i An integer represents the th n-i+1 Coefficient of subterm , Every two integers are separated by a space .
1 ≤ n ≤ 100, The absolute values of the coefficients of each degree of the polynomial do not exceed 100.
Output
common 1 That's ok , Output polynomials in the format described in the title .
The sample input
Examples #1: 5 100 -1 1 -3 0 10 Examples #2: 3 -50 0 0 1
Sample output
Examples #1: 100x^5-x^4+x^3-3x^2+10 Examples #2: -50x^3+1
Link here :http://noi.openjudge.cn/ch0113/solution/35197972/
Here is the code I passed :
#include <stdio.h>
int main() {
int n,m;
scanf("%d",&n);
int flag = 1;
for(int i=n;i>=0;i--) {
scanf("%d",&m);
if(m==0) continue; // The coefficient is 0 Just skip
if(i==n) { // The highest term of a polynomial
if(m==-1) printf("-"); // The coefficient is -1 The output minus sign of
else if(m!=1) printf("%d",m); // Other situations as long as they are not 1 Output as is
}else if(i==0) { // The lowest term of a polynomial
if(m==1) printf("+1");
else if(m==-1) printf("-1");
else if(m>0 && !flag) printf("+%d",m);
else if(m>0 && flag) printf("%d",m);
else if(m<0) printf("%d",m);
break; // Jump straight out of the loop
}else {
if(m==-1) printf("-"); // The coefficient is -1 The output minus sign of
else if(m==1) printf("+"); // The coefficient is 1 The output positive sign of
else if(m<0) printf("%d",m); // In other cases, negative numbers are output as is
else if(m>0) printf("+%d",m); // If it is a positive number, add a positive sign and output
}
if(i==1) printf("x"); // The special judgment index is 1 Output x
else if(i!=0) printf("x^%d",i);// The index is not 0 Just output it as it is
flag = 0;
}
return 0;
}I think there is something wrong with this problem , The code I submitted for the first time should be entered as 1 0 2 Yes, the output result is +2 Yes. accepted Of . The above code is the code submitted for the second time after processing , Output is 2, It's also passable .
Finally, the code of adding polynomials directly , The details are in the code :
#include <stdio.h>
#include <stdlib.h>
typedef struct polynomial {
int coefficient;
int exp;
struct polynomial * next;
}NODE, *PNODE;
void insert(PNODE L, int coefficient, int exp) {
PNODE s = (NODE*)malloc(sizeof(NODE));
s->coefficient = coefficient;
s->exp = exp;
s->next = NULL;
PNODE p = L->next, q = L;
while(p && p->exp > exp) { // Find the position where the first index is not greater than the index of the inserted node and use p Pointing to it
q = p;
p = p->next;
}
if(!p) { // Special judgement p Is it empty , That is, insert in the last case
q->next = s;
return;
}
if(p->exp == exp) { // Discuss that the index is equal to p The index pointing to the node is still less than p The indices pointing to nodes are processed separately
p->coefficient += coefficient;
free(s);
} else {
s->next = q->next;
q->next = s;
}
}
void input(PNODE &L) {
L = (NODE*)malloc(sizeof(NODE));
L->next = NULL;
int coefficient, exp;
printf(" Please enter coefficients and exponents ( Such as :\"2 3\" Express 2x^3):");
scanf("%d%d",&coefficient, &exp);
insert(L,coefficient,exp);
while(coefficient || exp) {
printf(" Please enter coefficients and exponents :");
scanf("%d%d",&coefficient, &exp);
insert(L,coefficient,exp);
}
}
void print(PNODE L) {
PNODE p = L;
int flag = 1;
while(p) {
if(p->coefficient==0) {
p = p->next;
continue;
}
if(p==L) { // The highest term of a polynomial
p = L->next;
if(p->coefficient==-1) printf("-"); // The coefficient is -1 The output minus sign of
else if(p->coefficient!=1) printf("%d",p->coefficient); // Other situations as long as they are not 1 Output as is
}else if(p->exp==0) { // The lowest term of a polynomial
if(p->coefficient==1) printf("+1");
else if(p->coefficient==-1) printf("-1");
else if(p->coefficient>0 && !flag) printf("+%d",p->coefficient);
else if(p->coefficient>0 && flag) printf("%d",p->coefficient);
else if(p->coefficient<0) printf("%d",p->coefficient);
break; // Jump straight out of the loop
}else {
if(p->coefficient==-1) printf("-"); // The coefficient is -1 The output minus sign of
else if(p->coefficient==1) printf("+"); // The coefficient is 1 The output positive sign of
else if(p->coefficient<0) printf("%d",p->coefficient); // In other cases, negative numbers are output as is
else if(p->coefficient>0) printf("+%d",p->coefficient); // If it is a positive number, add a positive sign and output
}
if(p->exp==1) printf("x");
else if(p->exp) printf("x^%d",p->exp); // As long as the index is not 0 Just output it as it is
flag = 0;
p = p->next;
}
printf("\n");
}
void combine(PNODE &L3, PNODE L1, PNODE L2) {
L3 = (NODE*)malloc(sizeof(NODE));
L3->next = NULL;
PNODE p = L1->next, q = L2->next, r = L3;
while(p && q) {
if(p->exp > q->exp) {
r->next = p;
p = p->next;
} else if(q->exp > p->exp) {
r->next = q;
q = q->next;
}else {
q->coefficient = q->coefficient + p->coefficient;
r->next = q;
q = q->next;
p = p->next;
}
r = r->next;
}
r->next = p ? p : q;
}
int main() {
PNODE L1,L2,L3;
printf(" Please enter the coefficient and exponent of the first polynomial , With (0,0) end :\n");
input(L1);
printf(" The output of the first polynomial is as follows :\n");
print(L1);
printf(" Please enter the coefficient and exponent of the second polynomial , With (0,0) end :\n");
input(L2);
printf(" The output of the second polynomial is as follows :\n");
print(L2);
combine(L3,L1,L2);
print(L3);
return 0;
}边栏推荐
- 11. Camera and lens
- 专访即构科技李凯:音视频的有趣、行业前沿一直吸引着我
- Stm32 paj7620u2 gesture recognition module (IIC communication) program source code explanation
- Cloud XR面临的问题以及Cloud XR主要应用场景
- SDLC software development life cycle and model
- mysql case when
- Automated test Po design model
- P2P 之 UDP穿透NAT的原理与实现
- 虚拟偶像代言产品出问题谁负责?
- H5测试点(思维导图)
猜你喜欢

【解决方案】Microsoft Edge 浏览器 出现“无法访问该页面”问题

我也是醉了,Eureka 延迟注册还有这个坑!
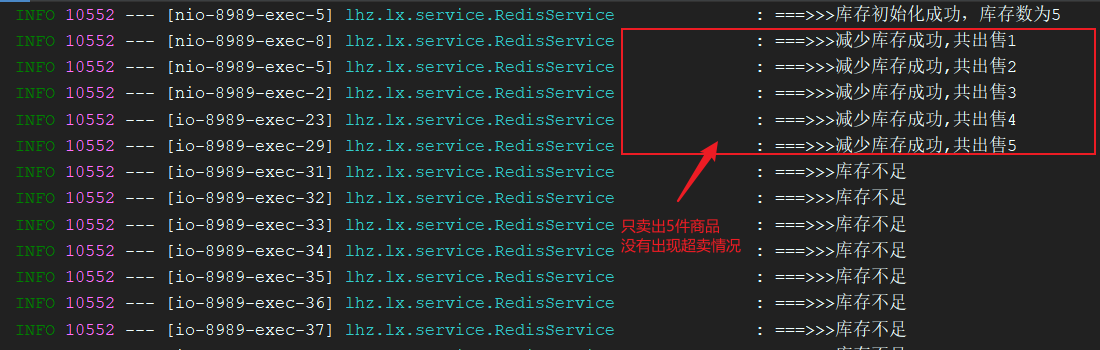
Redistemplate solves the problem of oversold inventory in the seckill system with high speed - redis transaction + optimistic lock mechanism

Ultimate doll 2.0 | cloud native delivery package

11. Camera and lens

面试官:说说 log.Fatal 和 panic 的区别

11、照相机与透镜

SVN客户端(TortoiseSVN)安装及使用说明

Idea essential plug-ins
什么是 IP SSL 证书,如何申请?
随机推荐
Redis source code and design analysis -- 15. RDB persistence mechanism
Sorting also needs to know the information and linked list
Idea 必备插件
I2C communication - sequence diagram
Go defer and recover simple notes
Redis源码与设计剖析 -- 17.Redis事件处理
为什么数字化未来取决于3D实时渲染
ROS学习笔记(四)ros 无法rosdep init 或者update解决方法
MySQL数据库常用命令
PageHelper还能结合Lambda表达式实现简洁的分页封装
go channel简单笔记
Notes on Flickr's dataset
Take you to a preliminary understanding of multiparty secure computing (MPC)
HCIP第一天实验
云流化和云桌面有什么关系
有没有什么不起眼却挣钱的副业?
New and malloc
实时云渲染有哪些优势
交友活动记录
11. Camera and lens