当前位置：网站首页>The most commonly used objective weighting method -- entropy weight method

Entropy is a physical concept of thermodynamics , It is a measure of the degree of chaos or disorder of the system , The larger the entropy, the more chaotic the system is （ That is, the less information you carry ）, The smaller the entropy, the more orderly the system is （ That is, the more information you carry ）. Information entropy refers to the concept of entropy in thermodynamics , Shannon called the amount of information contained in the source information entropy , Used to describe the average amount of event information , So in Mathematics , Information entropy is the expectation of the amount of information contained in an event （mean, Or mean , Or expectation , Is the probability of each possible result in the test multiplied by the sum of its results ）, According to the definition of expectation , It is conceivable that the formula of information entropy is ：

$H(X)=-\sum_{i=1}^{q}p(x_{i})log(p(x_{i}))$

among H It's information entropy ,q Is the number of source messages , $p(x_{i})$ It's the news $x_{i}$ Probability of occurrence .

1.2 Entropy weight method

Information is a measure of the order of a system , Entropy is a measure of the disorder of a system ; According to the definition of information entropy , For an indicator , Entropy can be used to judge the dispersion degree of an index , The smaller the information entropy , The greater the dispersion of the index , The impact of this index on Comprehensive Evaluation （ That's the weight ） The greater the , If the values of an indicator are all equal , Then the index does not play a role in the comprehensive evaluation . therefore , Information entropy can be used as a tool , Calculate the weight of each index , Provide basis for multi index comprehensive evaluation .

Literal paraphrase ： When we analyze a factor , Subjectively list some influential indicators , These indicators have some correlation with dependent variables , Whether it is positive or negative correlation , At the same amount of change , The value of each indicator has also changed , At some stage ,X1 Changed 1,X2 Changed 0.5, The dependent variable changes 1, From the perspective of relevance X1 The correlation ratio X2 Be big ,X1 Yes Y The impact of , Then come to see X1 and X2 The index value of , If we say that the proportion is the same ( One value divided by the sum of all values ) After normalization ,X1 It seems that the amount of change is relatively large , The greater the degree of data dispersion after normalization , such as [1 1.5 2] and [1.5 1.75 2] After normalization, it is [0.22 0.33 0.44] and [0.28 0.33 0.38], The dispersion of the former is greater than that of the latter . Although this method is simple , But it is very useful in the practical problems of enterprises , For example, the ability level of business personnel should be evaluated according to their benefit and output .

Two 、 The main steps of entropy weight method

2.1 Data standardization

First, each index is de dimensioned . Suppose given m Indicators ：

among

It is assumed that the standardized value of each indicator data is

2.2 Calculate the ratio of each index under each scheme

Set a certain level of indicators to have m Two level index , And has obtained n Annual data , Write it down as a matrix $Y_{ij}$ . Under the same index , Calculate the proportion of each year's value in the total value , The formula is as follows ：

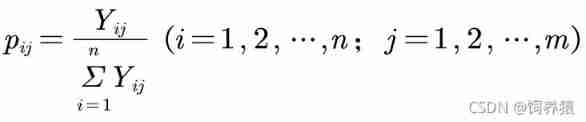
2.3 Find the information entropy of each index .

According to the definition of information entropy in information theory , The information entropy of a set of data is ：

2.4 Determine the weight of each indicator

According to the calculation formula of information entropy , The information entropy of each index is calculated as E1,E2,…,Em.

2.4.1 Calculate the weight of each index through information entropy ：

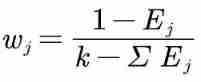
here k It refers to the number of indicators , namely k=m.

2.4.2 Calculate the weight by calculating the information redundancy ：

Then calculate the index weight ：

2.5 Finally, calculate the comprehensive score of each scheme

3、 ... and 、 Program （MATLAB）


X=[124.3000    2.4200   25.9800   19.0000    3.1000   79.0000   54.1000    6.1400    3.5700   64.0000
  134.7000    2.5000   21.0000   19.2500    3.3400   84.0000   53.7000    6.7400    3.5500   64.9600
  193.3000    2.5600   29.2600   19.3100    3.4500   92.0000   54.0000    7.1800    3.4000   65.6500
  118.6000    2.5200   31.1900   19.3600    3.5700  105.0000   53.9000    8.2000    3.2700   67.0100
   94.9000    2.6000   28.5600   19.4500    3.3900  108.0000   53.6000    8.3400    3.2000   65.3400
  123.8000    2.6500   28.1200   19.6200    3.5800  108.0000   53.3000    8.5100    3.1000   66.9900];
[n,m]=size(X);
for i=1:n
    for j=1:m
        p(i,j)=X(i,j)/sum(X(:,j));
    end
end
%%  Computation first  j  The entropy of each index  e(j)
k=1/log(n);
for j=1:m
    e(j)=-k*sum(p(:,j).*log(p(:,j)));
end
d=ones(1,m)-e; %  Computing information entropy redundancy 
w=d./sum(d) %  Find the weight  w

Four 、 summary

4.1 The use of entropy weight method

Entropy weight method is one of the most basic models in modeling competition , It is mainly used to solve evaluation problems （ for example ： Choose which option is best 、 Which athlete or employee performed better ）, Used to determine the weight of each indicator , Weights are used to calculate the final score .

4.2 The advantages of entropy weight method

Entropy method is to determine the index weight according to the variation degree of each index value , This is an objective weighting method , The deviation caused by human factors is avoided . Compared with those subjective assignment methods , Higher accuracy and objectivity , Can better explain the results obtained .

Subjective assignment ： Analytic hierarchy process , Efficacy coefficient method , Fuzzy comprehensive evaluation method , Composite index method

4.3 Disadvantages of entropy weight method

（1） The importance of the indicator itself is ignored , Sometimes the index weights determined will be far from the expected results , At the same time, entropy method can not reduce the dimension of evaluation index , That is, the entropy weight method conforms to the mathematical law and has strict mathematical significance , But the subjective intention of decision makers is often ignored .

（2） If the change of index value is very small or suddenly becomes larger and smaller , The entropy weight method has its limitations

Succeed in learning 、 Progress in learning ！ We study together and don't give up ~

Remember Sanlian ~ Your support is my biggest motivation ！！ Welcome to read previous articles ~

Xiao Bian's contact information is as follows , Welcome to communicate with you .

int[] arr=new int[]{4,8,3,2,6,5,1};
int[] index= new int[]{6,4,5,0,3,0,2,6,3,1};
String QQ = "";
    for (int i : index){
        QQ +=arr[i];
}
System.out.println(" Small make up the QQ:" + QQ);