Binary search

 

 
 

  

Two points search

   Binary search is also called half search . A halved search will N The two elements are divided into roughly the same two parts . Select the middle element and compare it with the found element , Or compare it with the search criteria , Find or find the half area of the next search . Reduce the scope to 1/2 So time complexity is O(log₂n）, But the premise of binary search is orderly , It is generally arranged from small to small .
 
 
The basic idea of binary search ：
In an ordered list （low, high, low<=high）, Take the intermediate record, i.e [(high + low) / 2] As the object of comparison .

• If the given value is equal to the key of the intermediate record , Then the search is successful
• If the given key is less than the middle value of the record , Then continue to search in the left half of the middle record
• If the given value is greater than the key of the intermediate record , Then continue to search in the right half of the middle record

Keep repeating the process , Until the search is successful , Or there is no record in the area you are looking for , To find the failure .
 
 
Features of binary search ：

1. The answer is monotonous ;
2. Questions with two-point answers often have fixed questions , such as ： Minimize the maximum value （ The minimum is the maximum ）, Find the maximum that satisfies the condition （ Small ） It's worth waiting for .

Binary search diagram

 
 

Binary search template

bool check(int x) {
    /* ... */} //  Check x Whether it satisfies certain properties 

//  Section [l, r] Divided into [l, mid] and [mid + 1, r] When using ：
//  When we will interval [l, r] Divide into [l, mid] and [mid + 1, r] when , The update operation is r = mid perhaps l = mid + 1;, Calculation mid There is no need to add 1.
int bsearch_1(int l, int r)
{
    
    while (l < r)
    {
    
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check() Judge mid Is the property satisfied 
        else l = mid + 1;
    }
    return l;
}
//  Section [l, r] Divided into [l, mid - 1] and [mid, r] When using ：
//  When we will interval [l, r] Divide into [l, mid - 1] and [mid, r] when , The update operation is r = mid - 1 perhaps l = mid;, In order to prevent the dead cycle , Calculation mid Need to add 1.
int bsearch_2(int l, int r)
{
    
    while (l < r)
    {
    
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

   In the first piece of code , if a[mid] ≥ x, Then according to the sequence a The monotonicity of ,mid Then the number will be bigger , therefore ≥ x The smallest number of cannot be in mid after , The feasible range should be reduced to the left half . because mid Or maybe the answer , Therefore, we should take r = mid. Empathy , if a[mid] < x, take l = mid + 1.
   In the second code , if a[mid] ≤ x, Then according to the sequence a The monotonicity of mid The previous number will be smaller , therefore ≤ x The maximum number of cannot be in mid Before , The feasible range should be reduced to the right half . because mid Or maybe the answer , Therefore, we should take l = mid. Empathy , if a[mid] > x, take r = mid - 1.

As shown in the above two codes , This dichotomy may take two forms ：

1. When narrowing down ,r = mid,l = mid + 1, When taking the intermediate value ,mid = (l + r) >> 1.
2. When narrowing down ,l = mid,r = mid - 1, When taking the intermediate value ,mid = (l + r＋1) >> 1.

   If you don't mid To distinguish between , Suppose the second code also uses mid = (l ＋r) >> 1, So when r - l be equal to 1 when , There is mid = (l + r) >> 1 = l. Next, if you enter l = mid Branch , The feasible range is not reduced , Create a dead cycle ; If enter r = mid - 1 Branch , cause l > r, A loop cannot be in the form of l = r end . Therefore, the two forms are matched mid It is necessary to adopt the method . The two forms shown in the above two pieces of code together constitute the implementation method of this dichotomy . Be careful , We use the right shift operation in the binary implementation >> 1, Not integer division /2. This is because the shift right operation is rounding down , Integer division is rounding to zero , When the binary range contains negative numbers, the latter does not work properly .
   Carefully analyze these two mid How to choose , We also found that ：mid = (l + r) >> 1 I won't get r This value ,mid = (l + r＋1) >> 1 I won't get l This value . We can use this property to deal with the case of no solution , Put the initial bisection interval [1, n] Expand to [1, n+1] and [0, n], hold a An out of bounds subscript of the array is included . If the last two points end at the expanded cross-border subscript , shows α The requested number does not exist in .

  
To make a long story short , The correct process for writing this dichotomy is ：

1. By analyzing specific problems , Determine which of the left and right halves is the feasible interval , as well as mid Which half belongs to .
2. According to the analysis , choice “r = mid, l = mid + 1, mid = (l＋r) >> 1” and “l = mid,r = mid - 1,mid = (l＋r＋1) >> 1” One of two supporting forms .
3. The two-part termination condition is l == r, This value is where the answer is .

   There are other dichotomous ways , use “l = mid + 1, r = mid-1” or “l = mid, r = mid” To avoid two forms , But it also caused the loss in mid The feasible range is not narrowed to the exact answer when the answer on the dot ends , Need to be dealt with additionally .
  C++ STL Medium lower_bound And upper_bound Function to find an integer in a sequence x In the subsequent .

 
 

Precision template ：

// Template I ： Real number field dichotomy , Set up eps Law 

// Make  eps  It is a number less than the accuracy of the topic . For example, the title says keep 4 Decimal place ,0.0001  Such . that  eps  You can set it to any number with five decimal places  0.00001- 0.00009  You can wait .

// Generally, in order to ensure the accuracy, we choose the accuracy /100  The decimal of , Setting the  eps= 0.0001/100 =1e-6

while (l + eps < r)
{
    
    double mid = (l + r) / 2;

    if (pd(mid))
        r = mid;
    else
        l = mid;
}

// Template II ： Real number field dichotomy , Method of specifying the number of cycles 

// Through a certain number of cycles to meet the accuracy requirements , This one is average  log2N <  Accuracy is enough .N  Is the number of cycles , Without exceeding the time complexity , You can choose to give  N  Multiplying by a factor makes the accuracy higher .

    for (int i = 0; i < 100; i++)
{
    

    double mid = (l + r) / 2;
    if (pd(mid))
        r = mid;
    else
        l = mid;
}

 
 

 
 

 
 

subject

Split chocolate

Topic link

Their thinking ：
Simple ideas , The maximum size of the side length is 100000; We can cite all the cases . Cut in descending order , Until you find the desired side length of chocolate .

When judging whether the side length meets the conditions ： Find a rectangle （h * w） The most divided square （len * len） The number of chocolates is ：

cnt = (h / len) \* (w / len)

But using a naive algorithm to enumerate the time complexity O(n)*O(n) =O(n²) Will timeout , So use 2 Split search method , This finds the largest one that meets the requirements .

It is used in monotonically increasing sequences a Search for <=x The largest number of （ namely x or x The precursor of ） that will do , The original condition here is <=x , We can replace it with verification .

 
 

#include <iostream>
using namespace std;
int N, K, H[100010], W[100010];

bool judge(int k){
    // Length of judgement k Whether the conditions are met  
  int sum = 0;
  for(int i = 0; i < N; i ++){
    
    sum += (H[i] / k) * (W[i] / k);
    if(sum >= K)// Return directly after reaching the request  
      return true;// accord with  
  }
  return false;// Do not conform to the  
}

int main()
{
    
  //  Please enter your code here 
  scanf("%d %d", &N, &K);
  for(int i = 0; i < N; i ++)
    scanf("%d %d", &H[i], &W[i]);
  
  int l = 1, r = 100001;
  while(l <= r){
    // Two points search  
    int mid = (l + r) / 2;
    if(judge(mid))
      l = mid + 1;
    else
      r = mid - 1;
  }
  printf("%d", r);
  return 0;
}

 
 

 
 

M Power root

Topic link

 
 
Topic analysis ：
This question involves precision , We use the precision version .
Let's design pd function ：pd Success , It must be pd Of mid eligible , And less than mid You must meet the conditions . So we have to be greater than mid Continue to find , Find a bigger mid.

double pd(double a,int m)
{
    
    double c = 1;
    while(m > 0)
    {
    
        c = c * a;
        m --;
    }
    if(c >= n)
        return true;
    else
        return false;
}

 
 

#include <cstdio>
#include <iostream>
using namespace std;

double n,l,r,mid;
double eps = 1e-8;

bool pd(double a, int m){
    
    double c = 1;
    while(m > 0){
    
        c = c * a;
        m --;
    }
    if(c >= n)
        return true;
    else
        return false;
}

int main(){
    
    int m;
    cin>>n>>m;

	// Set the bisection boundary 
    l = 0, r = n;

	// The real number is divided into two parts 
    while (l + eps < r){
    
        double mid = (l + r) / 2;
        if (pd(mid, m))
            r = mid;
        else
            l = mid;
    }

    printf("%.7f", l);
    return 0;
}

 
 

 
 

The number of times a number appears in a sort array

Topic link

Time complexity ：O(logn)

class Solution {
    
public:
    int getNumberOfK(vector<int>& nums , int k) {
    
        if(!nums.size())
            return 0;
        
        int l1 = 0, r1 = nums.size() - 1;
        while(l1 < r1){
    
            int mid = l1 + r1 >> 1;
            if(nums[mid] >= k)
                r1 = mid;
            else
                l1 = mid + 1;
        }
        
        int l2 = 0, r2 = nums.size() - 1;
        while(l2 < r2){
    
            int mid = l2 + r2 + 1 >> 1;
            if(nums[mid] <= k)
                l2 = mid;
            else
                r2 = mid - 1;
        }
        
        if(nums[l1] != k && nums[l2] != k)
            return 0;
        return l2 - l1 + 1;
    }
};

Use lower_bound and upper_bound function .

class Solution {
    
public:
    int getNumberOfK(vector<int>& nums , int k) {
    
        auto l = lower_bound(nums.begin(), nums.end(), k);
        auto r = upper_bound(nums.begin(), nums.end(), k);

        return r - l;
    }
};

 
 

 
 

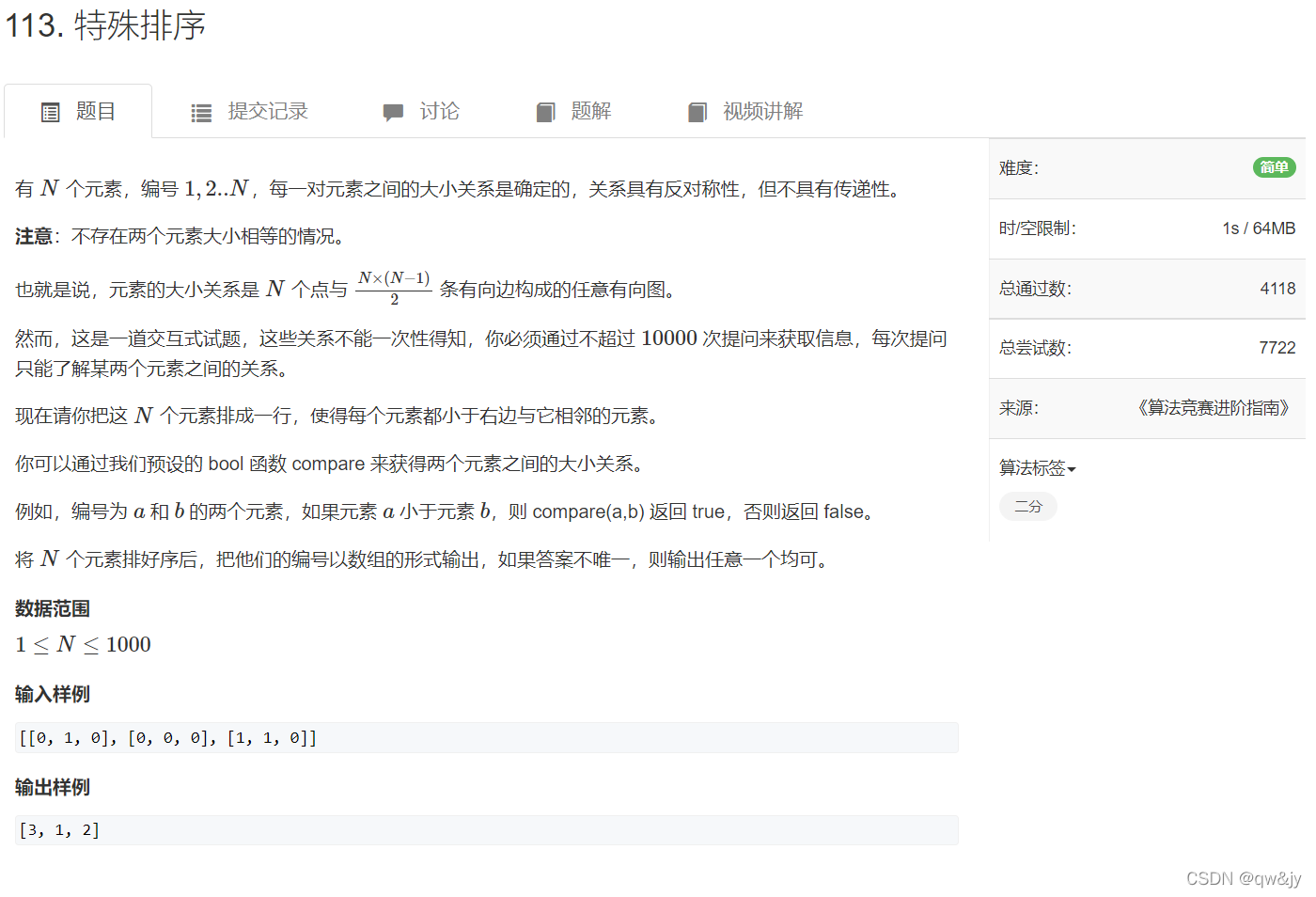
Special order

Topic link

Examples ：
Means for 3 Number of each group compare
compare（1,1）=0
compare（1,2）=1
compare（1,3）=0
compare（2,1）=0
compare（2,2）=0
compare（2,3）=0
compare（3,1）=1
compare（3,2）=1
compare（3,3）=0

Let's first assume vector There is an ordered set of elements in ：a, b, c, d, e
Now we're going to vector Insert f, How to determine the f The location of ？ Direct dichotomy mid = c, If f > c that f stay c,e Between , On the contrary, in a,c Between .( Find the insertion position through binary search )

// Forward declaration of compare API.
// bool compare(int a, int b);
// return bool means whether a is less than b.

class Solution {
    
public:
    vector<int> specialSort(int N) {
    
        vector<int> res;
        res.push_back(1);
        for(int i = 2; i <= N; i ++){
    
            int l = 0, r = res.size() - 1;
            while(l <= r){
    
                int mid = l + r >> 1;
                if(compare(res[mid], i))
                    l = mid + 1;
                else
                    r = mid - 1;
            }
            res.push_back(i);
            for(int j = res.size() - 2; j > r; j --)// Select Insert 
                swap(res[j], res[j + 1]);
        }
        return res;
    }
};

 
 

 
 

Don't modify the array to find duplicate numbers

Topic link

Divide and conquer + The drawer principle ： Altogether n+1 Number , The value range of each number is 1 To n, So at least one number will appear twice .

The idea of partition , The interval of the value of each number [1, n] Divide into [1, n / 2] and [n / 2 + 1, n] Two subintervals , Then count the number of numbers in the two intervals .
Note that the interval here refers to The value range of the number , instead of The array subscript .

After the division , There must be at least one interval in the left and right intervals , The number of numbers in the interval is greater than the interval length .
This can be illustrated by counter evidence ： If the number of numbers in both intervals is less than or equal to the interval length , Then the number of numbers in the whole interval is less than or equal to n, And have n+1 Number contradiction .

Therefore, we can classify the problem into one of the left and right subintervals , And because the number of numbers in the interval is greater than the interval length , According to the drawer principle , In this sub interval, there must be a number that appears twice .

By analogy , Each time we can reduce the length of the interval by half , Until the interval length is 1 when , We found the answer .

class Solution {
    
public:
    int duplicateInArray(vector<int>& nums) {
    
        int l = 1, r = nums.size() - 1;
        while(l < r){
    
            int mid = l + r >> 1;// Interval division [l, mid], [mid + 1, r]
            int s= 0;
            for(int i = 0; i < nums.size(); i++)// Count the number of numbers in the left half of the array [l ,mid]
                if(l <= nums[i] && nums[i] <= mid)
                    s ++;
            if(s > mid - l + 1)
                r = mid;
            else
                l = mid + 1;
        }
        return r;
    }
};