当前位置：网站首页>R language linear regression model fitting diagnosis outliers analysis of domestic gas consumption and calorie examples with self-test questions

R language linear regression model fitting diagnosis outliers analysis of domestic gas consumption and calorie examples with self-test questions

2022-06-30 01:05:00 【Extension Research Office】

Link to the original text ：http://tecdat.cn/?p=27474

The source of the original text is ： The official account of the tribal public

Consider our experiments 、 Some data were observed in the event y The situation of . We will observe the results y Explained as a random variable Y The implementation of the ：

Statistical models are for unknown parameters θ Of Y Specification of distribution . Usually , Observed value y = (y1, . . . , yn) ∈ Rn It's a vector , and Y = (Y1, . . . ., Yn) Is a random vector . under these circumstances , The statistical model is Y1 Specification of joint distribution , . . , Yn Until unknown parameters θ.

Mobile phone example

Observation examples ： yi = Student i Before the lecture 10 Check their mobile phones in minutes .
Model ：
In many experiments and situations , Observed value Y1, . . . , Yn Do not have the same distribution .Y1 The distribution of , .. . , Yn May depend on non random quantities x1, .. . , xn They are called covariates .

Example ： Do short students get higher marks in math exams ？

Yi = average ,xi = height
Model ：

Model fitting

We will describe the process of model fitting as follows ：
1. Model specifications —— Specify observations Y1, The distribution of .. . , Yn Reachable unknown parameter .

2. Estimation of unknown parameters of the model .
3. Reasoning —— This involves building confidence intervals and testing assumptions about parameters .
4. The diagnosis —— Check the fit between the model and the data .
“ Ideal ” The model should
• It is quite consistent with the observed data .
• Do not include unnecessary parameters .
• Easy to explain .

R Example in

Suppose we have data consisting of domestic gas consumption and average external temperature （ See the table below ）. Can the outside temperature be used to measure the amount of gas used in a home ？

We will Gas As a dependent variable ,Yi and Temp As covariates xi. Suppose we use a linear normal model to interpret the data ; among Yi It's independent N(µi, σ2), among µi = β1 + β2xi about i = 1, . . . , 26. For this model , We have

And then calculate MLE Use the following command . First , We merge the observation vectors Y And design matrix X：

> X <- cbind(1,dat$Temp)

You can use the following command to find ：

> qr(t(X)%*%X)$rank
[1] 2

As Have full rank , We can calculate its inverse ：

> solve(t(X)%*%X)

MLE β = It can be calculated as follows ：

> betahat

Then draw the model fit we can use


> lines(x=xs,y=btaht[1]+xs*beaht[2])

Besides , The sum of squared residuals (RSS) by


> RSS <- t(ehat)%*%ehat
> RSS

Last , We can calculate :

> sg2ht <- RSS/(26-2)
> sg2at

The diagnosis
coefficient

One way to measure the goodness of fit of a linear model is to check the coefficient of determination ; Let's explain now . In the simplest model with only intercept terms

We have RSS = ∑in=1(Yi - Y)2. Larger models with more parameters and large design matrices will have smaller RSS.
For models with intercept terms , The measure of linear model quality is

This is called the coefficient of determination or R2 statistic . Please note that ,0 ≤ R2 ≤ 1 and R2 = 1 Corresponding to “ perfect ” Model .

outliers

Outliers are observations that do not conform to the general pattern of the rest of the data . Outliers may be due to data logging errors 、 Data is the mixture of two or more populations and the model needs to be improved . We will assume a full rank design matrix .

Residual diagram

leverage

We may be interested in the extent to which each observation affects the model fit . for example , Consider the residuals e among

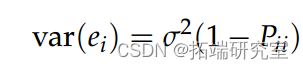
The lever corresponds to the variance of the observed residuals .

Cook distance

Another way to measure the impact of an observation is to consider its impact on the estimator β The change or effect of . One such measure is cook's distance

Is not to use the i An estimator calculated from observations . The rule of thumb is to look at Ci near 1 The observation value of .

Cook's explanation of distance

We will now study the residuals in more detail 、 The distance between lever and cook . Consider the following 4 Personal data set , Each data set has a normal linear model installed . Besides , The relationship between residual error and lever is also shown .

Red data points are suspicious data points , High leverage 、 High residual （ The absolute value ） Or both . The red line is a fitting including red data points , The black line is a fitting that does not include red data points .

Example

The data in the table shows 20 Percentage of total calories derived from complex carbohydrates in male diabetes patients on a high carbohydrate diet , And their age 、 Weight and calories as a percentage of protein .

We take the carbohydrate value as our reaction Yi, By age 、 Body weight and protein as covariates . And then we use Yi ∼ N(µi, σ2) Fitting normal linear model , among

then , To find the β Maximum likelihood estimator of , We need to solve :

> beta.hat <- solve(t(X)%*%X)%*%t(X)%*%y
> t(beta.hat)

An unbiased estimator of variance can be calculated RSS/(n - p), And used to calculate the standard deviation of each component .

> sqrt(diag(sig.sq.hat*solve(t(X)%*%X)))

The residual is

> summary(ehat)

R2 And its modified version R2 The coefficient is


> R2

> 1-(RS/(20-4))/(RS0/(20-1))

We can use R Medium lm Function to check these results , As shown below ：

> summary(mylm1)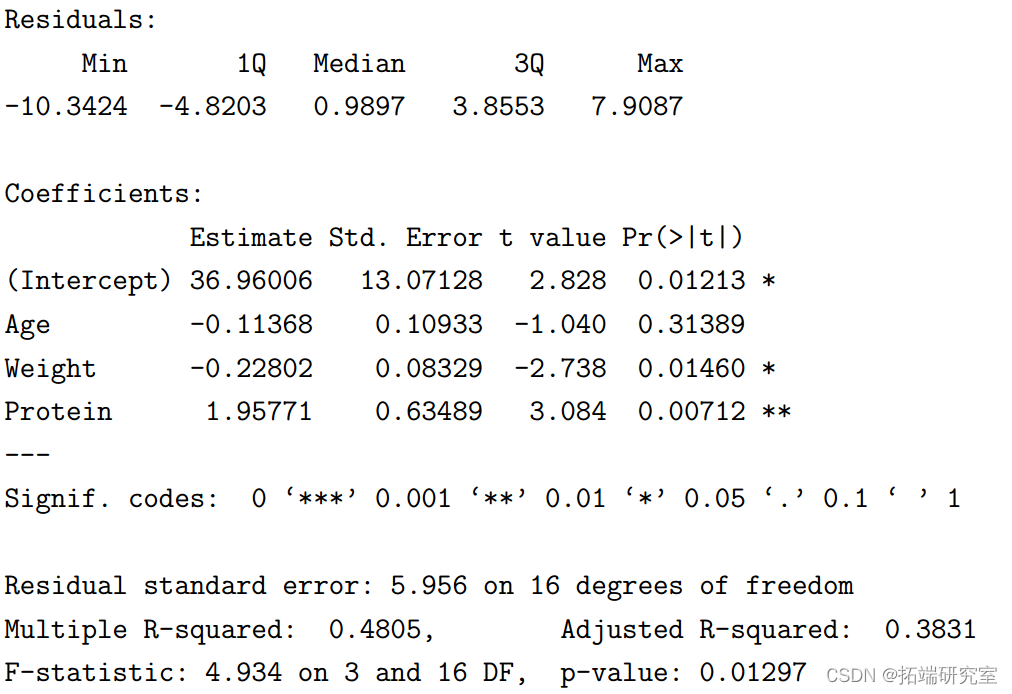

Next , We performed a one-way ANOVA test

> anova(mylm1)

Note the form of the output —— namely Sum Sq Based on the differences of the above models , namely


> sum(mym2$esiuls^2)-sum(mym3$reials^2)

Last ,R It can also generate some residual graphs for us , As shown below ：

> plot(mylm2)

Self test questions

Q1) (a) In R fit the normal linear model with:

Based upon the summary of the model, do you think that the model fits the data well? Explain your reasoning using the values reported in the R summary
(b) Perform a hypothesis test to ascertain whether or not to include the intercept term | use a 5% significance level. Include your code.
(c) Conduct a hypothesis test comparing the models:

E(Y ) = β1 against E(Y ) = β1 + β2x2 + β3x3 + β4x4
as a 5% level. Include your code
(d) By inspecting the leverages and residuals, identify any potential outliers. Name these data points by their index number. Give your reasoning as to why you believe these are potential outliers. You may present up to three plots if necessary.

Q2) We shall now consider a GLM with a Gamma response distribution.
(a) Show that a random variable Y where Y follows a Gamma distribution with probability density function:

is a member of the exponential family | taking the form a(φ) = φ. State the canonical link function and the variance function in terms of the expected response and the dispersion parameter.

(b) Show that the deviance for a GLM with a Gamma response distribution is

This is called the inverse link function.

(d) Write the components of the total score U1; : : : ; Up and the Fisher information matrix for this model.
(e) Given the observations y, what is a sensible initial guess to begin the IWLS algorithm in general?
(f) Manually write an IWLS algorithm to fit a Gamma GLM using your data, mydat, using the inverse link and same linear predictor in Q1a). Use the deviance as the convergence criteria and initial guess of β as (0:5; 0:5; 0:5; 0:5). Present your code and along with your final estimate of β and final deviance.
(g) Based on your IWLS results, compute φbD and φbp and the estimates of var(βb2). In R fit the model again with a Gamma response i.e.

> glm(y~x1+x2+x3,family=Gamma,data=mydat)

Note the capital G in Gamma. Verify the results with your IWLS results.
(h) Give a prediction for the response given by the model for x1= 13, x2= 5 x3= 0:255
and give a 91% confidence interval for this prediction. Include your code.
(i) Perform a hypothesis test between this model and another model with the same link and response distribution but with linear predictor η where ηi = β1 + β2xi1 + β3xi2 for i = 1; : : : ; n:
Use a 5% significance level. You may use the deviance function here. Include your code.
(j) Using your IWLS results, manually compute the leverages of the observations for this model | present your code (but not the values) and plot the leverages against the observation index number.
(k) Proceed to investigate diagnostic plots for your Gamma GLM. Identify any potential outliers | give your reasoning. Remove the most suspicious data point
| you must remove 1 and only 1 | and refit the same model. Compare and comment on the change of the model with and without this data point | you may wish to refer to the relative change in the estimated coefficients. You may present up to three plots if necessary.