[Discrete Mathematical period Review Series] Second and first order Logic (precate Logic)

1.Logique de premier ordre(Logique prédicative);
Mots individuels:Individus isolés,Peut être spécifique,Abstrait.Comme un homme.,La peinture,La pensée…
Prédicat:Représente la nature ou la relation entre les deux, par exemple:…C'est un programmeur AQueBÉlevé
Constante individuelle:Un mot désignant une personne spécifique ou spécifique
Variable individuelle:Nom de l'individu en général
Domaine individuel:Plage de valeurs des variables individuelles,Peut être limité,Ou infini. Comme un ensemble de nombres naturels
Total des domaines individuels:Le domaine individuel est composé de tout ce qui se trouve dans l'univers.
Constante de prédicat:Prédicat d'une nature ou d'une relation particulière
Variable prédicative:Prédicat abstrait ou générique
xDe natureF :Notez comme suit:F(x)
x,yA une relationL:Notez comme suit:L(x,y)
Nombre d'éléments:Le nombre de mots individuels contenus dans le prédicat est appelé.
Y comprisn(n≥1)Les prédicats des verbes individuels sont appelésnMéta - prédicat.Un prédicat unidimensionnel est une représentation de la nature d'un verbe.
Quandn≥2Heure,nLes méta - prédicats représentent les relations entre les mots individuels
0Méta - prédicat:Prédicat sans variable individuelle,Est de transformer une variable prédicative individuelle en constante prédicative individuelle

2.Quantificateur complet:

3.Quantificateur existentiel:

Exemple:

M（x）：xC'est humain., Prédicat de propriété

3. Alphabet symbolique logique de premier ordre

4.Item (s):

5.Formule atomique:Mise en placeR(x1,x2,…xn)C'est arbitraire.nMéta - prédicat,t1,t2,…, tn- Oui.,Est appeléR(t1,t2,…,tn).
Formule combinée(Formule prédicative): Formule abrégée

6. Variable de guidage :Formule combinée∀xAEt∃xADansx
Juridiction:Formule combinée∀xAEt∃xADansA
Les contraintes apparaissent: Dans la juridiction xToutes les occurrences de(x Limité par les variables guidées par le quantificateur correspondant )
Libre d'apparaître:A Présence d'autres variables qui n'apparaissent pas dans la contrainte （ Variable non liée par un Quantificateur ）
Exemple：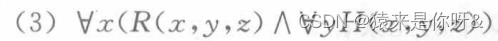

Formule fermée (Fermé):Si la formuleA Il n'y a pas de variable individuelle libre dans （ Il n'y a pas d'éléments non liés ）

8.ExplicationI: Ce qui est populaire, c'est que les éléments incertains (Élément,Fonctions,Prédicat)Assigner des valeurs

Compétences en résolution de problèmes: Mettez toutes les conditions à l'intérieur.
Affectation:Compte tenu de l'explicationI, Spécifiez un élément dans le champ individuel pour chaque variable individuelle qui apparaît librement dans la formule
Exemple

9. Validité logique (Yongzhen):Mise en placeA Est une formule prédicative ,SiA True under any Interpretation and any Assignment under that interpretation
Ambivalence(Toujours faux):,SiA False under any Interpretation and any Assignment under this Interpretation
Satisfaisant: S'il y a au moins une explication et qu'une affectation en vertu de cette explication AC'est vrai.

11.Équivalence:Mise en placeA、B Est deux formules dans la logique du premier ordre ,SiA<-→B Logique valide ,Notez comme suit:A<=>B
Théorèmes importants:

Note::A(x) Est une formule arbitraire avec une présence libre ,EtBNe contient pasx La liberté d'apparaître

Paradigme de l'orteil： Un quantificateur complet ou un quantificateur existant devant une formule prédicative.
Exemple:

Note:: Le but du changement de nom est d'éliminer certaines contraintes indépendantes d'un quantificateur, comme: （2）Questions, Accès facile aux orteils （Quantificateur）, Si vous pouvez avancer directement, vous n'avez pas besoin de changer d'élément. , Sinon, j'en ai besoin.
Bien sûr, le paradigme des orteils de la formule prédicative n'est pas unique ,Par exemple,（3） Vous pouvez changer de nom avant de le mentionner. ,Le résultat est également vrai
12.Fin:
Syllogisme Socrate“ Tout le monde meurt. .Socrate: C'est un homme.. Socrate va mourir.