深度学习方法求解平均场博弈论问题

背 景

Mean field games (MFG, 平均场博弈论)和Mean field control (MFC, 平均场控制论）可以模拟大量对象之间的博弈，探索在一个竞争的环境中，对象如何选择最优的决策。例如股市里大量根据其他用户行为交易股票的股民，海里游动的鱼群，在世界杯现场看足球赛的观众等。它们在物理、经济学和数据科学等各学科中发挥核心作用。虽然MFG的数学理论已经相当成熟，但数值方法的发展并没有跟上问题规模和海量数据集的增长。由于MFG通常不存在显式解，有效的数值算法至关重要。大多数现有的数值方法都使用网格，因此容易受到维数灾难的限制。

近些年来，结合机器学习方法对MFG和MFC问题进行求解得到了学术界的大量关注。尤其是针对解决具有复杂结构，高维度的问题。本文将介绍基于深度学习求解MFG和MFC的三类方法。

问题定义

MFG和MFC模型包括下列参数：

 

 

 

 

 

 

 

 

 

 

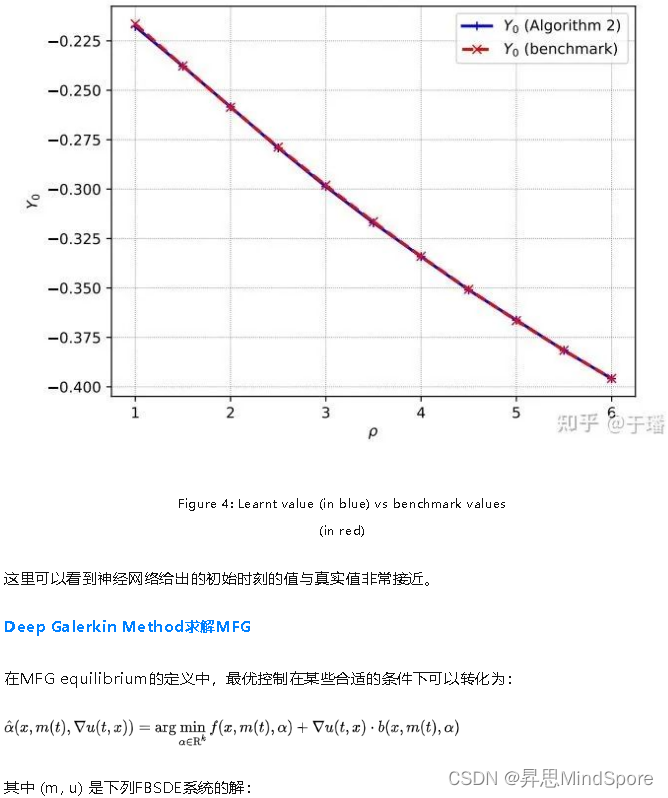
这里神经网络估计的最优控制和状态概率分布都与理论值相符合：

1. 最优控制是状态的线性函数；

2. 状态的概率分布会向0逐渐移动。

 总结与展望 

本文着重介绍了三种运用深度学习求解MFG和MFC相关问题的方法。第一个方法通过神经网络直接拟合控制函数，第二种方法通过Deep BSDE求解FBSDE,最后一个方法通过神经网络去求解偏微分方程，进而求解HJB方程与FKP方程组成的方程组。基于上述方法，学术界已经对多个高维度的复杂问题进行了各种尝试，取得了一些初步成果 。但是由于神经网络通常由多个项组成，因此是高度非凸优化问题。在训练过程中，损失函数中的各项可能会相互竞争，训练过程可能不是鲁棒和足够稳定的，无法保证收敛到全局最小值。为了解决这个问题，需要开发更加鲁棒的网络结构和训练算法。

目前MindSpore团队分别从物理驱动和数据驱动的AI方法出发，致力于在科学计算领域发展新的算法并开发高性能和易用的AI仿真框架，后续有机会再跟大家分享。

同时，我们也欢迎广大的AI科学计算爱好者和研究者加入我们，共同探索AI科学计算这一新课题。

参考文献：

[1] en.wikipedia.org/wiki/Fokker%25E2%2580%2593Planck_equation

[2] en.wikipedia.org/wiki/Hamilton%25E2%2580%2593Jacobi%25E2%2580%2593Bellman_equation

[3] papers.ssrn.com/sol3/papers.cfm%3Fabstract_id%3D2557457

[4] arxiv.org/abs/1811.08782

[5] DeepBSDE pnas.org/content/115/34/8505

[6] Optimal transport and crowd motion pnas.org/content/117/17/9183

MindSpore官方资料

GitHub : https://github.com/mindspore-ai/mindspore

Gitee : https : //gitee.com/mindspore/mindspore

官方QQ群 : 486831414