李宏毅机器学习（2017版）_P6-8：梯度下降

相关资料

开源内容：https://linklearner.com/datawhale-homepage/index.html#/learn/detail/13

开源内容：https://github.com/datawhalechina/leeml-notes

开源内容：https://gitee.com/datawhalechina/leeml-notes

视频地址：https://www.bilibili.com/video/BV1Ht411g7Ef

官方地址：http://speech.ee.ntu.edu.tw/~tlkagk/courses.html

1、梯度下降（Gradient Descent）定义

损失函数最小值求解：
$${\theta }^{\ast }=arg\min \min L(\theta )$$
$L:lossfunction（损失函数）\theta :parameters（参数）$
梯度下降:
分别计算初始点处，两个参数对 L的偏微分，然后 ${\theta }^0$减掉 $\eta$(Learning rates（学习速率）)乘上偏微分的值，得到一组新的参数。

2、调整学习率

2.1、恒定学习率问题

学习率太小（蓝色的线），损失函数下降的非常慢；学习率太大（绿色的线），损失函数下降很快，但马上就卡住不下降了；学习率特别大（黄色的线），损失函数就飞出去了；红色的就是差不多刚好，可以得到一个好的结果。

2.2、自适应学习率（Adaptive Learning Rates）

随着次数的增加，通过一些因子来减少学习率。
刚开始，初始点会距离最低点比较远，使用大一点的学习率，比较靠近最低点了，减小学习率。
例如：${\eta }^t=\frac{{\eta }^t}{\sqrt{t+1}}$，t是次数。随着次数的增加，${\eta }^t$减小。
**注意：**学习率不能是一个值通用所有特征，不同的参数需要不同的学习率

3、相关优化算法

3.1、Adagrad 算法

3.1.1、概念

Adagrad算法指每个参数的学习率都把它除上之前微分的均方根。

公式简化如下：

参数更新过程：

3.1.2、理论解释

• 对于单变量函数优化：
  

如果算出来的微分越大，则距离最低点越远。而且最好的步伐和微分的大小成正比。所以如果踏出去的步伐和微分成正比，它可能是比较好的。
梯度越大，就跟最低点的距离越远。

• 对于多变量函数优化：
  

最好的迭代步伐是：$\frac{一次微分}{二次微分}$，不止和一次微分成正比，还和二次微分成反比。
​
对于Adagrad算法，分母$\sqrt{{\sum }_{i=0}^t(g^i{)}^2}$就是希望在尽可能不增加过多运算的情况下模拟二次微分。（如果计算二次微分，在实际情况中可能会增加很多的时间消耗）。

3.2、随机梯度下降法（Stochastic Gradient Descent）

随机梯度下降法损失函数不需要处理训练集所有的数据，而是选取一个例子$x^n$处理（每次仅处理一个数据）。不需要像之前那样对所有的数据进行处理，只需要计算某一个例子的损失函数$Ln$，就可以更新梯度。
$$L=({\hat{y}}^n-(b+\sum _i{w}_i{x}_i^n){)}^2$$$${\theta }^i={\theta }^{i-1}-n\nabla L^n({\theta }^{i-1})$$
过程对比如下：

3.3、特征缩放（Feature Scaling）

3.3.1、概念

某个函数有多个输入特征，并且输入的特征数据分布的范围很不一样，建议把他们的范围缩放，使得不同输入的范围是一样的。$$y=b+w_1{x}_1+w_2{x}_2$$

3.3.2、原因

$x_1$对y的变化影响比较小，所以$w_1$对损失函数的影响比较小，$w_1$对损失函数有比较小的微分，所以$w_1$方向上是比较平滑的，同理$w_2$方向较陡峭。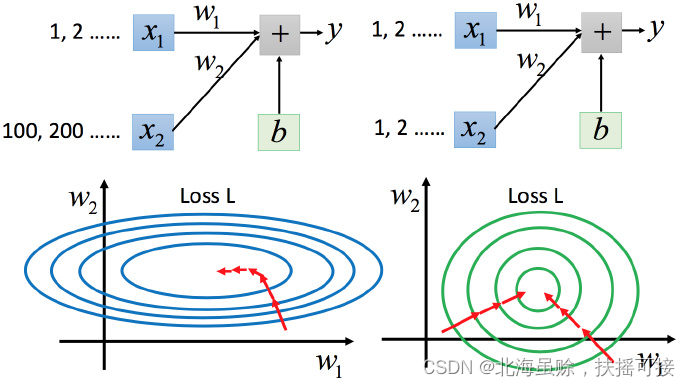

对于左边的情况，上面讲过这种狭长的情形不用Adagrad的话是比较难处理的。

• 两个方向上需要不同的学习率，同一组学习率会搞不定它。而右边情形更新参数就会变得比较容易。
• 左边的梯度下降并不是向着最低点方向走的，而是顺着等高线切线法线方向走的。但绿色就可以向着圆心（最低点）走，这样做参数更新也是比较有效率。

3.3.3、缩放方法

采用批量归一化方法进行缩放，缩放到标准正态分布。

上图每一列都是一个例子，里面都有一组特征。
对每一个维度i（绿色框）都计算平均数，记做$m_i$；还要计算标准差，记做${\sigma }_i$。
然后用第 r(特征)个例子中的第 i（数据）个输入，减掉平均数$m_i$，然后除以标准差${\sigma }_i$，得到的结果是所有的维数都是0，所有的方差都是1。（标准正态分布）

4、梯度下降的理论基础

4.1、下降可视化

在${\theta }^0$处，可以在一个小范围的圆圈内找到损失函数细小的${\theta }^1$，不断的这样去寻找。
关键在于如果在小圆圈内快速的找到最小值。

4.2、泰勒展开式

4.2.1、单变量泰勒展开式

若$h(x)$在 $x=x_0$点的某个领域内有无限阶导数（即无限可微分，infinitely differentiable），那么在此领域内有：

当x很接近$x_0$时，$h(x)\approx h(x_0)+h^{\prime }(x_0)(x-x_0)$。

4.2.2、多变量泰勒展开式

下面是两个变量的泰勒展开式：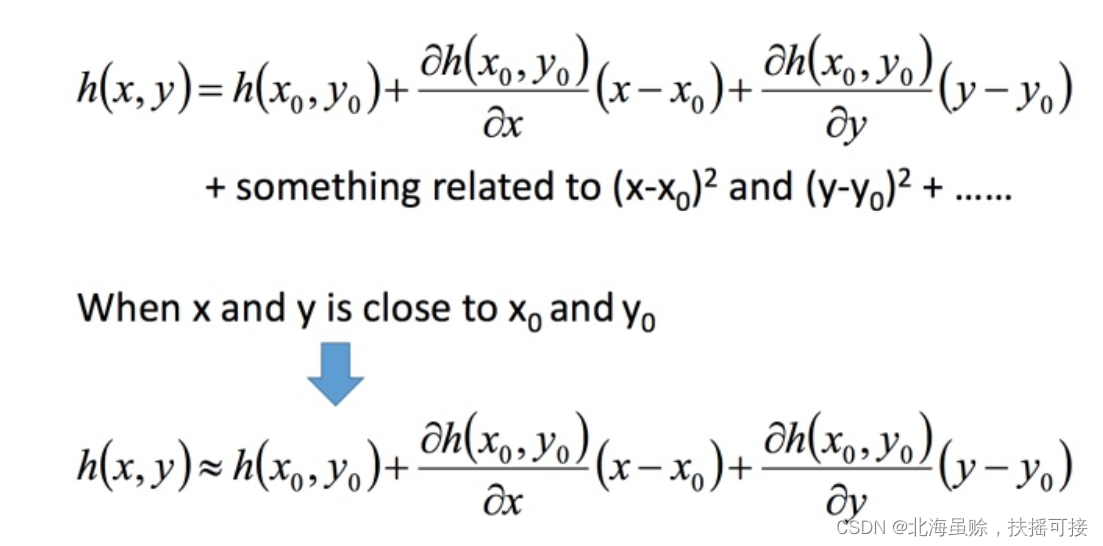

4.3、利用泰勒展开式求解最小值

将损失函数进行泰勒展开，同时略去无穷小项：

简化后如下：

利用向量点乘，求出最小值，推导出GD表达式：

注意：上述推导限制条件如下：
**推导前提：**泰勒展开式给的损失函数的估算值是要足够精确的，而这需要红色的圈圈足够小（也就是学习率足够小）来保证。所以理论上每次更新参数都想要损失函数减小的话，

4.4、梯度下降的限制

容易陷入局部极值 还有可能卡在不是极值，但微分值是0的地方 还有可能实际中只是当微分值小于某一个数值就停下来了，但这里只是比较平缓，并不是极值点。（难以确定真实情况）