Classic topics of leetcode tree (I)

427. Build a quadtree

https://leetcode-cn.com/problems/construct-quad-tree/

Ideas ： For a given nn Lattice of , Judge this first nn Whether all the grids are 0 Or both 1, If it is , Go directly back to a node , There is no need to create child nodes ; otherwise . Recursive creation 4 Child node , About the present nn A grid is divided into 4 individual n/2n/2 The rectangular , Then repeat the above steps
details ： To know n*n Whether all the grids are 0 Or both 1, You can create a prefix and an array first , Given (a,b) (c,d) These two points （ Top left and bottom right ） The elements of the rectangle and , Judge whether and are 0（ All elements are 0） Or equal to the area （ All elements are 1）; If not , According to (a,b) (c,d) Find the upper left and right corners of the four sub rectangles , Do recursive operations

/* // Definition for a QuadTree node. class Node { public boolean val; public boolean isLeaf; public Node topLeft; public Node topRight; public Node bottomLeft; public Node bottomRight; public Node() { this.val = false; this.isLeaf = false; this.topLeft = null; this.topRight = null; this.bottomLeft = null; this.bottomRight = null; } public Node(boolean val, boolean isLeaf) { this.val = val; this.isLeaf = isLeaf; this.topLeft = null; this.topRight = null; this.bottomLeft = null; this.bottomRight = null; } public Node(boolean val, boolean isLeaf, Node topLeft, Node topRight, Node bottomLeft, Node bottomRight) { this.val = val; this.isLeaf = isLeaf; this.topLeft = topLeft; this.topRight = topRight; this.bottomLeft = bottomLeft; this.bottomRight = bottomRight; } }; */

class Solution {
    
    public Node construct(int[][] grid) {
    
        int m=grid.length,n=grid[0].length;
        int[][] pre=new int[m+1][n+1];
        for(int i=1;i<=m;i++){
    
            for(int j=1;j<=n;j++){
    
                pre[i][j]=pre[i][j-1]+pre[i-1][j]+grid[i-1][j-1]-pre[i-1][j-1];
            }
        }
     

        return dfs(grid,pre,0,0,m-1,n-1);
    }
    public Node dfs(int[][] grid,int[][] pre,int a,int b,int c,int d){
    
        int sum=pre[c+1][d+1]-pre[a][d+1]-pre[c+1][b]+pre[a][b];
        int w=d-b+1,h=c-a+1;
        if(sum==0||sum==w*h)
            return new Node(grid[a][b]==1,true);// Leaf node  val The value depends on grid[a][b] yes 0 still 1
        Node root=new Node(true,false);// Nonleaf node 
        root.topLeft=dfs(grid,pre,a,b,a+h/2-1,b+w/2-1);// Rectangle in the upper left corner 
        root.topRight=dfs(grid,pre,a,b+w/2,a+h/2-1,d);
        root.bottomLeft=dfs(grid,pre,a+h/2,b,c,b+w/2-1);
        root.bottomRight=dfs(grid,pre,a+h/2,b+w/2,c,d);
        return root;
    }
}

Interview questions 04.06. The successor

https://leetcode.cn/problems/successor-lcci/

Ideas ： For one BST for , node X There are two situations for the follow-up of ：

1. X Right subtree of is not empty , be X Is followed by the smallest node in the right subtree
2. X The right subtree of is empty , be X Subsequent to X The first left ancestor node of Y（Y yes X The ancestor node of , also X stay Y In the left subtree ）

class Solution {
    
    public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
    
        if(p.right!=null){
    
            TreeNode node=p.right;
            while(node.left!=null)
                node=node.left;
            return node;
        }
        TreeNode successor=null;
        TreeNode node=root;
        while(node!=null){
    
            if(node.val>p.val){
    
                successor=node;//suc Point to p First right ancestor node of 
                node=node.left;
            }else{
    
                node=node.right;
            }
        }
        return successor;
    }
   
}
//O(n)
//O(1)

1022. Sum of binary numbers from root to leaf

https://leetcode.cn/problems/sum-of-root-to-leaf-binary-numbers/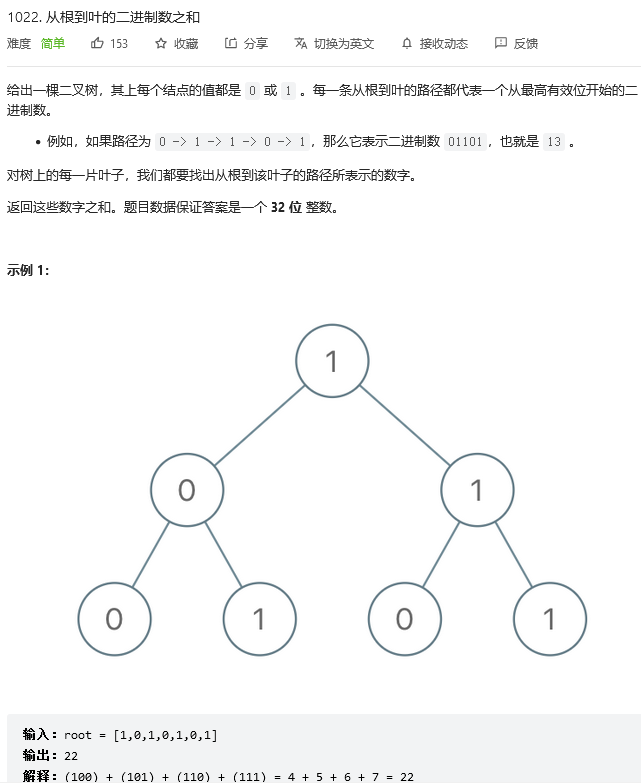

Ideas ： Accumulate data from top to bottom , For leaf nodes , Directly return the node value ; For non leaf nodes , Returns the cumulative sum of the values of its left subtree ,sum=sum<<1|val : Indicates that will val Added to the value formed on the right side of the binary

class Solution {
    
   
    public int sumRootToLeaf(TreeNode root) {
    
        return dfs(root,0);
    }
    public int dfs(TreeNode root,int sum){
    
        if(root==null)
            return 0;
        sum=sum<<1|root.val;
        if(root.left==null&&root.right==null){
    
            return sum;
        }
        return dfs(root.left,sum)+dfs(root.right,sum);
    }
}
//O(n)
//O(n)

450. Delete nodes in binary search tree

https://leetcode.cn/problems/delete-node-in-a-bst/

Ideas ： Delete BST One of the nodes in x, Divided into the following 4 In this case （ Suppose the node to be deleted x Exist in BST in ）：

1. x It's a leaf node
2. x Only the left child nodes
3. x Only the right child nodes
4. x There are both left and right child nodes

class Solution {
    
    public TreeNode deleteNode(TreeNode root, int key) {
    
        if(root==null){
    
            return null;
        }
        if(root.val<key){
    // The current node value is less than key  Go to root Delete from the right subtree of 
            root.right=deleteNode(root.right,key);
        }else if(root.val>key){
    // The current node value is greater than key  Go to root Delete from the left subtree of 
            root.left=deleteNode(root.left,key);
        }else if(root.val==key){
    // At present root A node is a node to be deleted 
            if(root.left==null&root.right==null){
    // The current node is a leaf node   Delete directly 
                return null;
            }else if(root.left==null){
    // The current node has no left child nodes   Replace with the right child node root
               return root.right;
           }else if(root.right==null){
    // The current node has no right child node   Replace with the left child node root
               return root.left;
           }else{
    // Current node root There are left and right child nodes   Replace with the smallest node in the right subtree root 
               TreeNode tmp=root;//tmp Keep the original root
               root=findMin(tmp.right);// Replace with the smallest node in the right subtree root 
               root.right=deleteMin(tmp.right);// Delete the subtree of the smallest node as the right subtree 
               root.left=tmp.left;// The original root The left subtree of the node is used as the new root The left subtree of the node 
           }

        }
        return root;
    }
    // Looking to node The smallest node in the subtree whose node is the root 
    public TreeNode findMin(TreeNode node){
    
        if(node.left==null){
    
            return node;
        }
        return findMin(node.left);
        
    }
    // Delete with node Is the smallest node in the subtree of the root node 
    public TreeNode deleteMin(TreeNode node){
    
        if(node.left==null){
    
            return node.right;
        }
        node.left=deleteMin(node.left);
        return node;
    }
}
//O(n)
//O(n)

530. The minimum absolute difference of binary search tree

https://leetcode.cn/problems/minimum-absolute-difference-in-bst/

Ideas ： Yes BST An ascending sequence can be obtained by traversing the middle order , The simplest thing to do is to use a list, Middle order traversal records the values of each node , Go over it again list Find the minimum difference between adjacent elements ; The optimization approach is not to use list, Instead, a pre Variable records the value of the previous node , Then, the minimum difference between the current node and the previous node is continuously updated , After updating the difference , The current node becomes pre

class Solution {
    
    int pre=-1;
    int min=Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
    
        dfs(root);
        return min;
    }
    public void dfs(TreeNode root){
    
        if(root==null){
    
            return;
        }
        if(root.left!=null){
    
            dfs(root.left);
        }
        if(pre==-1){
    
            pre=root.val;
        }else{
    
            min=Math.min(min,root.val-pre);
            pre=root.val;
        }
        if(root.right!=null){
    
            dfs(root.right);
        }
    }
}
//O(n)
//O(n)

99. Restore binary search tree

https://leetcode.cn/problems/recover-binary-search-tree/

Ideas : First pair BST Do middle order traversal , And use a list Record the nodes traversed in sequence , Then find the two nodes that need to be exchanged ; With 1 2 3 4 5 6->1 5 3 4 2 6 For example ,2 and 5 There was an exchange , How to find out which elements are exchanged ？ Traverse the array after exchange , If for the first time find nums[i]>nums[i+1], that nums[i] It must be one of the two （5）, For another element , Then you need to continue to traverse back , the last one Meet the conditions nums[i]>nums[i+1] Of nums[i+1] It's just another element （2）, After finding these two elements , Exchange the values of these two nodes

class Solution {
    
    List<TreeNode> list=new ArrayList<>();
    public void recoverTree(TreeNode root) {
    
        inorder(root);
        TreeNode x=null,y=null;
        for(int i=0;i<list.size()-1;i++){
    
            if(list.get(i).val>list.get(i+1).val){
    
                y=list.get(i+1);
                if(x==null){
    
                    x=list.get(i);
                }
            }
        }
        int tmpVal=x.val;
        x.val=y.val;
        y.val=tmpVal;
    }
    public void inorder(TreeNode root){
    
        if(root==null){
    
            return;
        }
        inorder(root.left);
        list.add(root);
        inorder(root.right);
    }
}
//O(n)
//O(n)

1008. A binary search tree is constructed by preorder traversal

https://leetcode.cn/problems/construct-binary-search-tree-from-preorder-traversal/

Ideas 1： Recursive create , Each time the first element in the current subarray is root node , Then find the boundary between the left and right subtrees , Then locate the range of the left and right subtrees according to the dividing line

class Solution {
    
    public TreeNode bstFromPreorder(int[] preorder) {
    
        return bstFromPreorder(preorder,0,preorder.length-1);
    }
    public TreeNode  bstFromPreorder(int[] preorder,int start,int end){
    
        if(start>end){
    
            return null;
        }
        TreeNode root=new TreeNode(preorder[start]);
        start++;
        int tmp=start;
        while(start<=end){
    // Find the boundary between the left and right subtrees   At the end of the cycle start perform root Right child of 
            if(preorder[start]>root.val){
    
                break;
            }
            start++;
        }
        root.left=bstFromPreorder(preorder,tmp,start-1);
        root.right=bstFromPreorder(preorder,start,end);
        return root;
    }
}
//O(n^2)  The cumulative number of boundary lookups is n^2
//O(n)

Ideas 2： It is not necessary to find the boundary between the left and right subtrees every time , Pass the upper and lower bounds as parameters , Nodes within the upper and lower bounds are the upper layer root Child nodes of , Otherwise, it's not

class Solution {
    
    int len;
    int index;
    int[] preorder;
    public TreeNode bstFromPreorder(int[] preorder) {
    
        this.len=preorder.length;
        this.preorder=preorder;
        return bstFromPreorder(Integer.MIN_VALUE,Integer.MAX_VALUE);
    }
    public TreeNode  bstFromPreorder(int lowerBound,int upperBound){
    
        if(index==len){
    // All elements have been added to BST in 
            return null;
        }
        int cur=preorder[index];
        if(cur<lowerBound||cur>upperBound){
    // The currently traversed element is not in [low,up] Within the scope of   to flash back   Show the current cur Not on the next floor 
            return null;// In recursion root Left child node or right child node of 
        }
        index++;// At present cur It's the upper floor root Child nodes of 
        TreeNode root=new TreeNode(cur);
        root.left=bstFromPreorder(lowerBound,cur);//root The node is the upper bound of the left subtree 
        root.right=bstFromPreorder(cur,upperBound);//root The node is the lower bound of the right subtree 
        return root;
    }
}
//O(n) 
//O(n)

199. Right side view of binary tree

https://leetcode.cn/problems/binary-tree-right-side-view/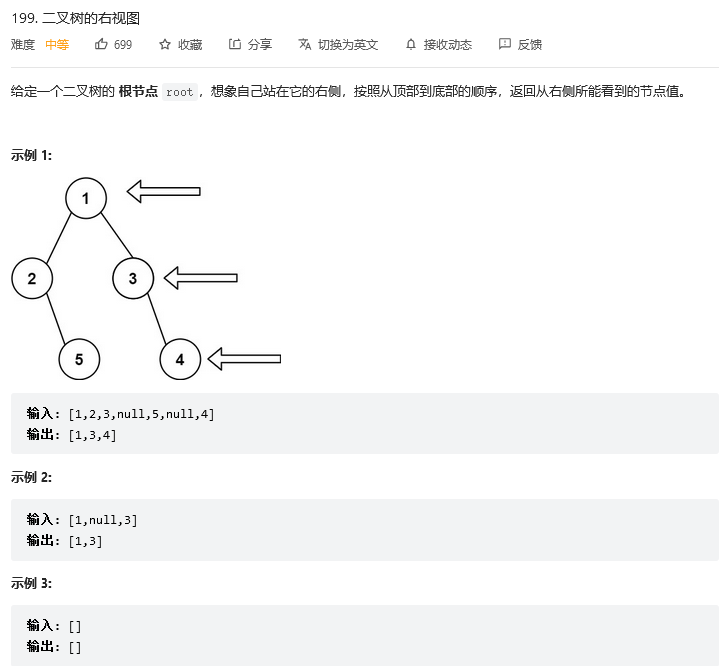

Ideas 1：BFS, Ergodic time , First add the right child node of the next layer to the queue , So when traversing to the next layer , The first node is the node that the current layer can see

class Solution {
    
    public List<Integer> rightSideView(TreeNode root) {
    
        List<Integer> ans=new ArrayList<>();
        if(root==null){
    
            return ans;
        }
        LinkedList<TreeNode> q=new LinkedList<>();
        q.offer(root);
        while(!q.isEmpty()){
    
            int sz=q.size();
            for(int i=0;i<sz;i++){
    
                TreeNode node=q.poll();
                if(i==0){
    // Because each layer adds the right child node first   So the first one is the node that the current layer can see 
                    ans.add(node.val);
                }
                if(node.right!=null){
    // Add the right child node first 
                    q.offer(node.right);
                }
                if(node.left!=null){
    
                    q.offer(node.left);
                }
            }
        }
        return ans;
    }
}
//O(n)
//O(n)

Ideas 2：DFS, Perform depth traversal in the order of right and left root , The current depth is the same as the number of elements in the collection , Then add the current node to the collection

class Solution {
    
    List<Integer> ans=new ArrayList<>();
    public List<Integer> rightSideView(TreeNode root) {
    
        dfs(root,0);
        return ans;
    }
    public void dfs(TreeNode root,int depth){
    
        if(root==null){
    
            return;
        }
        if(ans.size()==depth){
    // Because only one node will be added to each layer   So when depth and ans Add when the size is the same 
            ans.add(root.val);
        }
        dfs(root.right,depth+1);// First access the right child node 
        dfs(root.left,depth+1);

    }
        
}
//O(n)
//O(n)

513. Find the value in the lower left corner of the tree

Ideas 1： DFS, Use a formal parameter to represent the number of layers currently traversed , Another variable is used to indicate the number of updates , Only the first node on the left of each layer will be updated , Therefore, only when the number of updates is the same as the number of layers

class Solution {
    
    int ans;
    int d;
    public int findBottomLeftValue(TreeNode root) {
    
        dfs(root,0);
        return ans;
    }
    public void dfs(TreeNode root,int depth){
    
        if(root==null){
    
            return;
        }
        if(depth==d){
    // Only take the first value of each layer 
            ans=root.val;
            d++;
        }
        dfs(root.left,depth+1);
        dfs(root.right,depth+1);
    }
}
//O(n)
//O(n)

Ideas 2：BFS, When traversing a layer, only the first node of the layer is updated each time

class Solution {
    
  
    public int findBottomLeftValue(TreeNode root) {
    
       int ans=0;
       LinkedList<TreeNode> q=new LinkedList<>();
       q.offer(root);
       while(!q.isEmpty()){
    
           int sz=q.size();
           for(int i=0;i<sz;i++){
    
               TreeNode node=q.poll();
               if(i==0){
    // Update only the first node of each layer 
                   ans=node.val;
               }
               if(node.left!=null){
    
                   q.offer(node.left);
               }
               if(node.right!=null){
    
                   q.offer(node.right);
               }
           }
       }
       return ans;
    }
    
}
//O(n)
//O(n)

671. The second smallest node in a binary tree

https://leetcode.cn/problems/second-minimum-node-in-a-binary-tree/

Ideas ： The root node is the smallest node in the entire tree ,DFS If the current node is found node Is greater than or equal to ans Explain with node All values in the subtree of the root node are greater than or equal to ans, Go straight back to ; If there is no return , And there is the current node node.val>minVal, Update page 2 Small value ans

class Solution {
    
    int ans=-1;// The first 2 Small value 
    int rootVal;
    public int findSecondMinimumValue(TreeNode root) {
    
        rootVal=root.val;//rootVal The smallest is the smallest 
        dfs(root);
        return ans;
    }
    public void dfs(TreeNode root){
    
        if(root==null){
    
            return;
        }
        if(ans!=-1&&root.val>=ans){
    // The first 2 The small value has been updated and the current node value >=ans  Note the node values in the subtree with the current node as the root are greater than or equal to ans  Go straight back to 
            return;
        }
        if(root.val>rootVal){
    // The current node value is greater than the minimum value   The current value is the th possible 2 Small value 
            ans=root.val;
        }
        dfs(root.left);
        dfs(root.right);
    }
}
//O(n)
//O(n)