当前位置:网站首页>Overview of common loss functions for in-depth learning: basic forms, principles and characteristics
Overview of common loss functions for in-depth learning: basic forms, principles and characteristics
2022-06-22 20:45:00 【Xinyi 2002】
from : Deep learning beginners
Supervised learning in machine learning is essentially given a series of training samples , Try to learn The mapping relation of , Make a given , Even if this Not in the training sample , Can also get as close to the truth as possible Output . And the loss function (Loss Function) Is a key part of this process , be used for Measure the output of the model The real The gap between , Point out the direction for the optimization of the model .
This article will introduce machine learning 、 Several loss functions commonly used in classification and regression in deep learning , Including the loss of mean square deviation Mean Squared Loss、 Average absolute error loss Mean Absolute Error Loss、Huber Loss、 Quantile loss Quantile Loss、 Cross entropy loss function Cross Entropy Loss、Hinge Loss Hinge Loss. This paper mainly introduces the basic forms of various loss functions 、 principle 、 Characteristics, etc .
Catalog
Preface
Mean square error loss Mean Squared Error Loss
Average absolute error loss Mean Absolute Error Loss
Huber Loss
Quantile loss Quantile Loss
Cross entropy loss Cross Entropy Loss
Hinge loss Hinge Loss
summary
Preface
Before the beginning of the text , Let's talk about Loss Function、Cost Function and Objective Function The difference and connection . These three terms are often used interchangeably in the context of machine learning .
Loss function Loss Function Usually For a single training sample , Given a model output And a real , The loss function outputs a real value loss
Cost function Cost Function Usually For the entire training set ( Or in use mini-batch gradient descent It's a mini-batch) Total loss of
Objective function Objective Function Is a more general term , Represents any function that you want to optimize , For machine learning and non machine learning ( For example, operational research optimization )
In a word, the relationship between the three is :A loss function is a part of a cost function which is a type of an objective function.
Because the loss function and the cost function are only different for the sample set , Therefore, the term loss function is used uniformly in this paper , But the relevant formulas below actually use the cost function Cost Function In the form of , Please pay attention to .
Mean square error loss
Basic form and principle
Mean square error Mean Squared Error (MSE) The loss is machine learning 、 One of the most commonly used loss functions in deep learning regression tasks , Also known as L2 Loss. Its basic form is as follows
Intuitively understand the loss of mean square deviation , The minimum value of this loss function is 0( When the prediction is equal to the real value ), The maximum is infinity . The following figure is for real values , Different predictions Variation diagram of mean square deviation loss of . The horizontal axis is a different predictor , The vertical axis is the loss of mean square deviation , You can see that with the absolute error between the prediction and the real value An increase in , The loss of mean square error increases quadratic .

The assumptions behind
In fact, under certain assumptions , We can use maximum likelihood to get the form of mean square loss . hypothesis The error between the model prediction and the real value obeys the standard Gaussian distribution ( ), Then give one The model outputs the true value The probability of is
Further, let's assume that the data set N The two sample points are independent of each other , Then all Output all true values Probability , Likelihood Likelihood, For all Tired multiplication
402 Payment Required
Usually for the convenience of calculation , We usually maximize the log likelihood Log-Likelihood
Remove and Irrelevant first item , Then it is transformed into minimizing negative log likelihood Negative Log-Likelihood
402 Payment Required
You can see that this is actually the form of mean square deviation loss . in other words Under the assumption that the error between the model output and the real value obeys Gaussian distribution , The minimum mean square loss function is essentially consistent with the maximum likelihood estimation , So in a scenario where this assumption can be satisfied ( For example, return ), Mean square loss is a good choice of loss function ; When this assumption cannot be satisfied ( Such as the classification ), The loss of mean square deviation is not a good choice .
Squared absolute error loss
Basic form and principle
Mean absolute error Mean Absolute Error (MAE) Is another commonly used loss function , Also known as L1 Loss. Its basic form is as follows
402 Payment Required
Similarly, we can visualize the loss function as shown in the figure below ,MAE The minimum loss is 0( When the prediction is equal to the real value ), The maximum is infinity . You can see that with the absolute error between the prediction and the real value An increase in ,MAE The loss increases linearly

The assumptions behind
Similarly, we can get by maximizing likelihood under certain assumptions MAE The form of loss , hypothesis The error between the model prediction and the real value obeys the Laplace distribution Laplace distribution( ), Then give one The model outputs the true value The probability of is
From the above derivation MSE Similar to , The negative log likelihood we can get is actually MAE The form of loss
MAE And MSE difference
MAE and MSE The main difference as a loss function is :MSE Loss compared with MAE It usually converges faster , but MAE Loss for outlier More robust , That is, less vulnerable to outlier influence .
MSE Often than MAE Can converge faster . When using gradient descent algorithm ,MSE The gradient of loss is , and MAE The gradient of loss is , namely MSE Gradient of scale Will vary with the size of the error , and MAE Gradient of scale It remains 1, Even in absolute error When I was very young MAE Gradient of scale Also for 1, This is actually very detrimental to the training of the model . Of course, you can alleviate this problem by dynamically adjusting the learning rate during the training process , But overall , The difference between the loss function gradients leads to MSE In most cases, it is better than MAE Converges faster . This is also MSE More popular reasons .
MAE about outlier more robust. We can understand this from two perspectives :
The first angle is to intuitively understand , The picture below is MAE and MSE The loss is drawn in the same picture , because MAE The relationship between loss and absolute error is linear ,MSE Loss and error are squared , When the error is very large ,MSE The loss will be far greater than MAE Loss . So when there is a very large error in the data outlier when ,MSE There will be a very big loss , It will have a great impact on the training of the model .

The second angle is from the assumption of two loss functions ,MSE It is assumed that the error follows Gaussian distribution ,MAE It is assumed that the error follows the Laplace distribution . The Laplace distribution itself is for outlier more robust. Refer to the below ( source :Machine Learning: A Probabilistic Perspective 2.4.3 The Laplace distribution Figure 2.8), When... Appears on the right side of the right figure outliers when , The Laplace distribution is much less affected than the Gaussian distribution . Therefore, the Laplace distribution is assumed MAE Yes outlier The Gaussian distribution is assumed MSE more robust.

Huber Loss
Above we have introduced MSE and MAE Losses and their respective advantages and disadvantages ,MSE Loss converges quickly but is susceptible to outlier influence ,MAE Yes outlier More robust but slow convergence ,Huber Loss Is a kind of MSE And MAE Combine , Take the loss function of both advantages , Also known as Smooth Mean Absolute Error Loss . The principle is simple , Is when the error is close to 0 When using MSE, Use when the error is large MAE, Formula for
In the above formula yes Huber Loss A super parameter of , The value of is MSE and MAE The location of the two lost connections . The first item on the right of the equal sign of the above formula is MSE Part of , The second is MAE part , stay MAE Part of the formula is To ensure the error when MAE and MSE The values of are the same , And then guarantee Huber Loss Loss is continuously differentiable .
The picture below is At the time of the Huber Loss, You can see in the In fact, it is MSE Loss , stay and The interval is MAE Loss .

Huber Loss Characteristics
Huber Loss Combined with the MSE and MAE Loss , When the error is close to 0 When using MSE, Make the loss function differentiable and the gradient more stable ; Use when the error is large MAE Can reduce the outlier Influence , Make training right outlier More robust . The disadvantage is that you need to set an additional Hyperparameters .
Quantile loss
Quantile regression Quantile Regression It is a very useful regression algorithm in practical application , The usual regression algorithm is to fit the expectation or median of the target value , Quantile regression can be achieved by giving different quantiles , Fit the different quantiles of the target value . For example, we can fit multiple quantiles , Get a confidence interval , As shown in the figure below ( The picture comes from a quantile regression code of the author demo Quantile Regression Demo)

Quantile regression is achieved by using quantile loss Quantile Loss To achieve this , The quantile loss form is as follows , Type in the r Quantile coefficient .
How do we understand this loss function ? The loss function is a piecewise function , take ( overestimate ) and ( underestimate ) Separate the two situations , And give different coefficients . When when , Underestimated losses are greater than overestimated losses , And vice versa when , An overestimated loss is greater than an underestimated loss ; Quantile loss is realized Different coefficients are used to control the losses of overestimation and underestimation , And then realize quantile regression . Specially , When when , The quantile loss degenerates into MAE Loss , You can see it here MAE Loss is actually a special case of quantile loss — Median regression ( It also explains why MAE Loss pair outlier More robust :MSE Regression expectation ,MAE Return to the median , Usually outlier The impact on the median is smaller than that on the expected value ).
The following figure shows taking different quantiles 0.2、0.5、0.6 Visualization of three different quantile loss functions obtained , You can see 0.2 and 0.6 In the case of overestimation and underestimation, the loss is different , and 0.5 It's actually MAE.

Cross entropy loss
The loss functions introduced above are all loss functions suitable for regression problems , For the classification problem , The most commonly used loss function is the cross entropy loss function Cross Entropy Loss.
Two classification
Consider two categories , In the second category we usually use Sigmoid Function to compress the output of the model to (0, 1) Within the interval , Used to represent a given input , The probability that the model is judged to be a positive class . Because there are only two categories , So we also get the probability of negative classes .
Combine the two equations into one
Suppose the data points are independent and identically distributed , Then the likelihood can be expressed as
Log the likelihood , Then add a minus sign to minimize the negative log likelihood , Is the form of cross entropy loss function
402 Payment Required
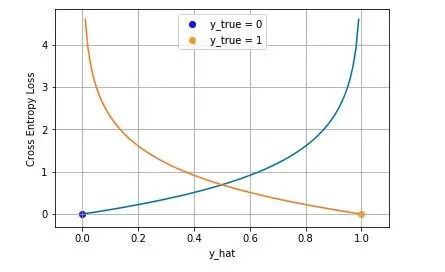
The following figure is a visualization of the cross entropy loss function of two categories , The blue line is the target value of 0 The loss of different outputs , The yellow line is the target value of 1 The loss of time . It can be seen that the loss is smaller when it is close to the target value , As the error gets worse , Losses are growing exponentially .
Many classification
In multi category tasks , The derivation of cross entropy loss function is the same as that of binary classification , What changes is the real value Now it's a One-hot vector , At the same time, the compression of the model output is changed from the original Sigmoid Replace function with Softmax function .Softmax The function limits the output range of each dimension to Between , At the same time, the output sum of all dimensions is 1, Used to represent a probability distribution .
among Express K One of the categories , The same assumption is that data points are independent and identically distributed , The negative log likelihood can be obtained as
because It's a one-hot vector , Except that the target class is 1 The output on other categories is 0, Therefore, the above formula can also be written as
402 Payment Required
among Is the sample Target class of . Usually, this cross entropy loss function applied to multi classification is also called Softmax Loss perhaps Categorical Cross Entropy Loss.
Cross Entropy is good. But WHY?
Why not use mean square error loss in classification ? When introducing the loss of mean square deviation, we mentioned that in fact, the loss of mean square deviation assumes that the error obeys Gaussian distribution , This assumption cannot be satisfied under the classification task , So the effect will be very poor . Why cross entropy loss ? There are two ways to explain this , From the perspective of maximum likelihood , That is, our derivation above ; Another angle is that the loss of cross entropy can be explained by information theory :
Suppose for the sample There is an optimal distribution It really shows the probability that this sample belongs to each category , So we want the output of the model As close to this optimal distribution as possible , In information theory , We can use KL The divergence Kullback–Leibler Divergence To measure the similarity between the two distributions . Given the distribution And distribution , Of the two KL The divergence formula is as follows
The first term is distribution The entropy of information , The second term is distribution and Cross entropy of . The optimal distribution And output distribution Into the and obtain
Because we want the two distributions to be as close as possible , So we minimize KL The divergence . At the same time, because the first item of information entropy in the above formula is only related to the optimal distribution itself , Therefore, in the process of minimization, we can ignore , Become minimized
402 Payment Required
We don't know the optimal distribution , But the target value in the training data You can view it as An approximate distribution of
402 Payment Required
This is the loss function for a single training sample , If you consider the entire dataset , be
You can see The results are derived by minimizing the cross entropy and using the maximum The result of likelihood is consistent .
Hinge loss
Hinge loss Hinge Loss Is another two class loss function , Apply to maximum-margin The classification of , Support vector machine Support Vector Machine (SVM) The loss function of the model is essentially Hinge Loss + L2 Regularization . The formula of hinge loss is as follows
402 Payment Required
The picture below is Is a positive class , namely when , Schematic diagram of hinge loss of different outputs

You can see when Positive class , The negative output of the model will have a greater penalty , When the model output is positive and at There will also be a smaller penalty in the interval . That is, hinge loss not only punishes the wrong prediction , And if the prediction is correct but the confidence is not high, a penalty will be given , Only those with high confidence will have zero loss . The intuitive understanding of using hinge loss is to Find a decision boundary , Make all data points correctly by this boundary 、 Be classified with high confidence .
summary
This paper introduces several loss functions which are most commonly used in machine learning , The first is the loss of mean square error for regression Mean Squared Loss、 Average absolute error loss Mean Absolute Error Loss, The difference between the two and the combination of the two Huber Loss, Then there is the quantile loss applied to quantile regression Quantile Loss, It is shown that the mean absolute error loss is actually a special case of quantile loss , In the classification scenario , This paper discusses the most commonly used cross entropy loss function Cross Entropy Loss, It includes forms under two categories and multiple categories , The cross entropy loss function is explained from the point of view of information theory , At last, the application in SVM Medium Hinge Loss Hinge Loss. The visualization code related to this article is in here .
Limited by time , There are many other loss functions not mentioned in this article , For example, apply to Adaboost Exponential losses in the model Exponential Loss,0-1 Loss function, etc . In addition, there is usually a regular term in the loss function (L1/L2 Regular ), These regular terms are part of the loss function , The complexity of the model is reduced by constraining the absolute value of the parameters and increasing the sparsity of the parameters , Prevent model over fitting , This part is not expanded in detail in this article . If you are interested, you can refer to relevant materials for further understanding .That’s all. Thanks for reading.
Recommended reading
use Python among Plotly.Express The module draws several charts , I was really amazed !!
New generation reptile weapon — Playwright
100 Common indicators and terms for data analysis
Share 、 Collection 、 give the thumbs-up 、 I'm looking at the arrangement ?




边栏推荐
- 三维天地助力实验室夯实完整质量体系管理
- A detailed solution to mysql8.0 forgetting password
- From perceptron to transformer, a brief history of deep learning
- A Dynamic Near-Optimal Algorithm for Online Linear Programming
- AAAI 2022 | traditional Gan can be interpreted after modification, and the interpretability of convolution kernel and the authenticity of generated image are guaranteed
- [observation] innovation in the software industry has entered a "new cycle". How can we make a new start in the changing situation?
- 完全背包如何考虑排列问题
- 什么?你居然不会微信分身
- 支持在 Kubernetes 运行,添加多种连接器,SeaTunnel 2.1.2 版本正式发布!
- Random talk about redis source code 122
猜你喜欢

Teach you how to create SSM project structure in idea

【已解决】--go_out: protoc-gen-go: Plugin failed with status code 1.

他98年的,我玩不过他...

One picture decoding opencloudos community open day

Three months of self-taught automatic test, salary from 4.5K to 15K, who knows what I have experienced?
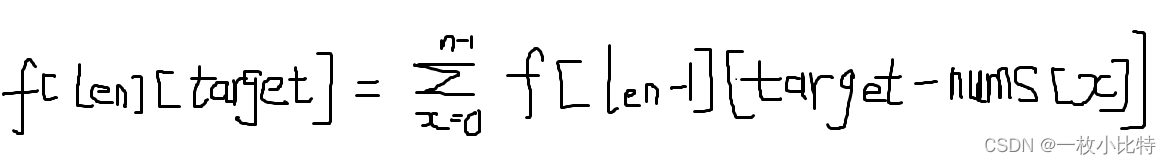
完全背包如何考慮排列問題
阿里云视频点播播放出错,控制台访问出现code:4400

智能计算之神经网络(BP)介绍

数字化转型的失败原因及成功之道

Simple integration of client go gin 11 delete
随机推荐
A detailed solution to mysql8.0 forgetting password
AAAI 2022 | 传统GAN修改后可解释,并保证卷积核可解释性和生成图像真实性
A Dynamic Near-Optimal Algorithm for Online Linear Programming
Oh, my God, it's a counter attack by eight part essay
MySQL Basics - functions
理财产品在双休日可以赎回吗?
Random talk on redis source code 119
89-oracle SQL写法与优化器缺陷一例
经典面试题:一个页面从输入url到呈现过程
[observation] innovation in the software industry has entered a "new cycle". How can we make a new start in the changing situation?
支持在 Kubernetes 运行,添加多种连接器,SeaTunnel 2.1.2 版本正式发布!
怎样实现网页端im即时通讯中的@人功能
How to consider the arrangement of complete knapsack
Using qtest for data set test performance test GUI test
完全背包如何考慮排列問題
Nestjs 集成 config module 与 nacos 实现配置化统一
Redis持久化的几种方式——深入解析RDB
EasyDSS问题及解决方案汇总
软件压力测试有哪些方法,如何选择软件压力测试机构?
92-几个用match_recognize SQL写法示例