当前位置：网站首页>二叉树神级遍历：Morris遍历
二叉树神级遍历：Morris遍历
2022-07-01 03:14:00 【苡荏】
二叉树的Morris遍历
1. 创建二叉树
typedef struct BiTNode{
int data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
//前序创建二叉树
void createBiTree(BiTree *T){
int value;
cin>>value;
if (value == 0)
*T = NULL;
else{
*T = (BiTree)malloc(sizeof(BiTNode));
if(!*T)
exit(OVERFLOW);
(*T)->data = value;
createBiTree(&(*T)->lchild);
createBiTree(&(*T)->rchild);
}
}
1 2 4 0 0 5 0 0 3 6 0 0 7 0 0 构建二叉树
2. 常规遍历
//前序遍历
void PreOrderTraverse(BiTree T){
if(T==NULL)
return;
cout<<T->data<<" ";
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
//中序遍历
void InOrderTraverse(BiTree T){
if(T==NULL)
return;
InOrderTraverse(T->lchild);
cout<<T->data<<" ";
InOrderTraverse(T->rchild);
}
//后序遍历
void PostOrderTraverse(BiTree T){
if(T==NULL)
return;
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
cout<<T->data<<" ";
}
//测试
int main(){
BiTree T;
createBiTree(&T);
PreOrderTraverse(T); // 1 2 4 5 3 6 7
cout<<endl;
InOrderTraverse(T); // 4 2 5 1 6 3 7
cout<<endl;
PostOrderTraverse(T); // 4 5 2 6 7 3 1
return 0;
}
3. Morris遍历
- 获得Morris序的执行过程：
- 记当前节点为current（初始current = head），如果current没有左子树（current.left = null），则current向右移动（current = current.right），
- 当current有左子树（current.left != null），找到current左子树最右侧的节点（记为mostRight），
- 如果mostRight.right = null，则将mostRight的right指针指向current，即mostRight.right = current，此时current向左移动，
- 如果mostRight.right = current，则将mostRight的right指针置为null，即mostRight.right = null，此时current向右移动，
- current = null时，运行终止。
- 每次记录下current的节点最终得到Morris序。
举例演示：
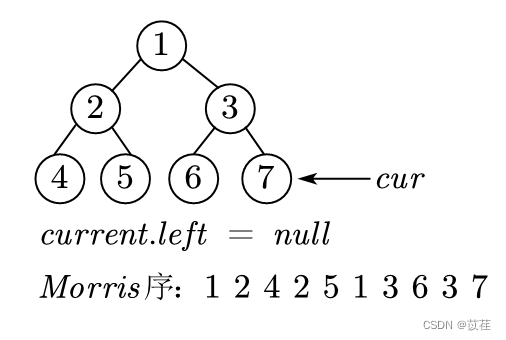
//获取Morris序列
void morris(BiTree T){
if(T==NULL)
return;
BiTree cur = T; // 初始化cur=T头节点
BiTree mostRight = NULL; // 初始化mostRight=NULL
while(cur != NULL){
mostRight = cur->lchild; //mostRight=cur的左孩子
cout<<cur->data<<" "; // 打印Morris序列
if(mostRight!=NULL){
while(mostRight->rchild!=NULL && mostRight->rchild!=cur){
mostRight = mostRight->rchild; // 将mostRight移动到cur左孩子的最右节点处
}
if(mostRight->rchild == NULL){
// mostRight的右节点为NULL
mostRight->rchild = cur; // 指向cur
cur = cur->lchild; // cur左移 下接continue直接下一次循环
continue;
} else {
mostRight->rchild = NULL; // 否则mostRight置NULL
}
}
cur = cur->rchild; // 在没有左子树或执行mostRight->rchild=NULL后执行
}
}
Morris序的特点：
1. 节点无左子树，则在Morris序中只出现一次，
2. 节点有左子树，则在Morris序中出现两次。下面，根据得到的Morris序做先序、中序、后序遍历：
1. 先序遍历：在Morris序中第一次出现时进行打印，第二次不打印，
2. 中序遍历：在Morris序中出现一次的立刻打印，出现二次的在第二次时打印，
3. 后序遍历：在Morris序中出现两次的节点且出现在第二次时进行处理：逆序打印该节点的左子树的右边界，最后逆序单独打印二叉树的右边界。
//Morris先序遍历：
void morrisPre(BiTree T){
if(T==NULL)
return;
BiTree cur = T;
BiTree mostRight = NULL;
while(cur != NULL){
mostRight = cur->lchild;
if(mostRight!=NULL){
// 左子树不为NULL，必然Morris序列中存在两次节点
while(mostRight->rchild!=NULL && mostRight->rchild!=cur){
mostRight = mostRight->rchild;
}
if(mostRight->rchild == NULL){
// Morris序列中两次节点第一次出现的情况进行data打印
cout<<cur->data<<" ";
mostRight->rchild = cur;
cur = cur->lchild;
continue;
} else {
mostRight->rchild = NULL;
}
} else{
// Morris序列中只能有一次的情况进行data打印
cout<<cur->data<<" ";
}
cur = cur->rchild;
}
}
//Morris中序遍历：
void morrisIn(BiTree T){
if(T==NULL)
return;
BiTree cur = T;
BiTree mostRight = NULL;
while(cur != NULL){
mostRight = cur->lchild;
if(mostRight!=NULL){
// 左子树不为NULL，必然Morris序列中存在两次节点
while(mostRight->rchild!=NULL && mostRight->rchild!=cur){
mostRight = mostRight->rchild;
}
if(mostRight->rchild == NULL){
// Morris序列中两次节点第一次出现
mostRight->rchild = cur;
cur = cur->lchild;
continue;
} else {
// 第二次
mostRight->rchild = NULL;
}
}
cout<<cur->data<<" "; // 打印中序序列节点
cur = cur->rchild;
}
}
//Morris后序遍历：
- Morris序：1 2 4 2 5 1 3 6 3 7
- 在第二次出现2的时候逆序打印2的左子树的右边界为4，
- 在第二次出现1的时候逆序打印1的左子树的右边界为5,2，
- 在第二次出现2的时候逆序打印3的左子树的右边界为6，
- 最后逆序打印该二叉树的右边界为7,3,1。
- 得到后序遍历结果为：4,5,2,6,7,3,1。
为保证空间复杂度为O(1)，在逆序打印右边界的时候，必须对边界节点右指针的指向进行调整。
// 从now开始，只考虑右指针，将其作为单链表的next，将这个单链表逆序，返回最后一个节点
BiTree reverseEdge(BiTree T){
BiTree pre = NULL;
BiTree next = NULL;
while(T!=NULL){
next = T->rchild;
T->rchild = pre;
pre = T;
T = next;
}
return pre;
}
// 以T节点为首的树，逆序打印树的右边界
void printEdge(BiTree T){
BiTree tail = reverseEdge(T);
BiTree cur = tail;
while(cur!=NULL){
cout<<cur->data<<" ";
cur = cur->rchild;
}
reverseEdge(tail);
}
//后序序列
void morrisPost(BiTree T){
if(T==NULL)
return;
BiTree cur = T;
BiTree mostRight = NULL;
while(cur != NULL){
mostRight = cur->lchild;
if(mostRight!=NULL){
// 左子树不为NULL，必然Morris序列中存在两次节点
while(mostRight->rchild!=NULL && mostRight->rchild!=cur){
mostRight = mostRight->rchild;
}
if(mostRight->rchild == NULL){
// Morris序列中两次节点第一次出现
mostRight->rchild = cur;
cur = cur->lchild;
continue;
} else {
// 出现两次且第二次出现时
mostRight->rchild = NULL;
printEdge(cur->lchild); // 进行处理
}
}
cur = cur->rchild;
}
// 结束后，逆序打印该二叉树的右边界
printEdge(T);
}
4. 时空复杂度
时间复杂度：O(n)
空间复杂度：O(1)
——————END-2022-06-26——————
边栏推荐
猜你喜欢
Latest interface automation interview questions
Huawei operator level router configuration example | configuration optionA mode cross domain LDP VPLS example
Hal library setting STM32 interrupt
Cookie＆Session
Multithreaded printing
Redis tutorial
第03章_用户与权限管理
不用加减乘除实现加法
A few lines of transaction codes cost me 160000 yuan
后台系统页面左边菜单按钮和右边内容的处理,后台系统页面出现双滚动
随机推荐
The best learning method in the world: Feynman learning method
Design of serial port receiving data scheme
Cloud native annual technology inventory is released! Ride the wind and waves at the right time
Detailed list of errors related to twincat3 ads of Beifu
EtherCAT原理概述
Go tool cli for command line implementation
Introduction and installation of Solr
C＃实现图的深度优先遍历--非递归代码
Analyze datahub, a new generation metadata platform of 4.7K star
第03章_用戶與權限管理
Cookie＆Session
go实现命令行的工具cli
IEDA 右键源码文件菜单简介
Hal library operation STM32 serial port
Redis分布式锁的8大坑
EtherCAT简介
串口接收数据方案设计
pytest-fixture
JS日常开发小技巧（持续更新）
【读书笔记】《文案变现》——写出有效文案的四个黄金步骤