Large factory interview machine learning algorithm (0): Feature Engineering | data preprocessing

The data is divided into buckets （ Separate boxes ）

Concept
Data bucket division is a data preprocessing technology , By discretizing continuous variables , Improve model performance .

significance

1. Discrete features are more important for outliers Robustness , Especially avoid Extreme outliers Interference of ;
2. Model after feature discretization A more stable , Not because of the characteristic value Slight change And change the result ;
3. Sparse vector inner product multiplication is fast , Algorithm Speed faster , It's also convenient Storage .

Barrel separation method

1. Supervised ：best-ks Split barrel and chi square split barrel
2. Unsupervised ： Equidistant barrel 、 Equal frequency bucket 、 Clustering bucket

Chi square is divided into barrels

The basic idea
Bottom up discretization method based on merging , Initially, each value is used as a sub box , Calculate the chi square value of adjacent intervals , Merge the interval with the lowest chi square value , Until the termination condition .

principle ： Chi square test

The application of chi square test in sub box
The core idea ： The smaller the chi square value, the more similar the distribution .
With “ Age ” Is the variable to be divided ,“ Default or not ” Take the predictive variable as an example .

1. To merge ages , First, age Sort , Then calculate the chi square value of each possible box combination .
   With 20+25 Take the combination as an example , Suppose the age is 20 still 25 It has no significant impact on whether it defaults , therefore In default p yes 15/33, Non defaulting p yes 18/33, from E=np Expect , Then use the formula to calculate 20+25 Combined chi square value .
   Extension ：$E=\frac{RT\ast CT}{n}$
   
2. Combine the combination with the smallest chi square value , And continue to calculate , Until the termination condition .
3. Termination conditions ：
   Limit on the number of boxes （ Generally, it can be set to 5）;
   Threshold of chi square stop ： You can choose a confidence of 0.9、0.95、0.99, freedom df=(R-1)(C-1), It's better than that 2.

Equidistant barrel

Global uniform statistics bucket （split_value_stat）
Map values to Equal size The range of . Ensure that features fall on each bucket The probability is the same . Such as ：

import numpy as np
#  Generate  20  individual  0-99  Random integer between 
small_counts = np.random.randint(0, 100, 20)
#  Carry out box splitting operation ,  By dividing the data by  10  be assigned to  0-9  in total  9  In a box ,
#  The returned result is the number of the box to which the corresponding data should be divided 
np.floor_divide(small_counts, 10)
#  return ： array([7,1,6,6,0,6,0,6,7,1,4,6,3,2,2,7,3,7,1])

shortcoming ： It may lead to a large number of values in some intervals , Some are very few .

As an example, divide barrels evenly （split_value_stat_pos）
Different from the overall situation , Select the positive example data and divide the barrels evenly .

Example log Statistical bucket （split_value_stat_pos_log）
What is different from the normal example is , The given probability distribution is log Distribution . It is applicable to the situation that numbers span multiple orders of magnitude , Take the count of log value , Such as ：

#  Construct an example of an array with a larger interval , You can take logarithm  log10  To separate boxes 
large_counts = [296, 8286, 64011, 80, 3, 725, 867, 2215, 7689, 11495, 91897, 44, 28, 7971, 926, 122, 22222]
np.floor(np.log10(large_counts))
#  return ：array([2.,3.,4.,1.,0.,2.,2.,3.,3.,4.,4.,1.,1.,3.,2.,2.,4.])

Equal frequency bucket

It is also called sorting barrels by Quantile , Map values to intervals , Make the number of values contained in each interval roughly the same . have access to Pandas Library get quantile , Such as ：

large_counts = [296, 8286, 64011, 80, 3, 725, 867, 2215, 7689, 11495, 91897, 44, 28, 7971, 926, 122, 22222]
#  Map the data to the quantile of the required number 
pd.qcut(large_counts, 4, labels=False)
#  Calculate the data of the specified quantile point 
large_counts_series = pd.Series(large_counts)
large_counts_series.quantile([0.25, 0.5, 0.75]
'''  return ： 0.25 122.0 0.50 926.0 0.75 8286.0 dtype:float64 '''

Clustering bucket

according to xgb Of get_split_value_histogram Function to obtain histogram, Take the split node value of the feature as split_value.
notes ：

1. Not every feature will have an appropriate split node value ;
2. A feature may be used multiple times in the same tree , Split many times ;
3. Finally, take the split value of the same feature on all trees as the bucket .

Dimensionless

Data normalization

min-max normalization

z-score

Data regularization

Simply speaking , Standardization deals with data according to the columns of characteristic matrix , The eigenvalues of samples are converted to the same dimension .
Regularization is to process data according to the rows of the characteristic matrix , Its purpose is to facilitate the point multiplication of sample vectors or the calculation of other kernel functions , In other words, they are transformed into “ Unit vector ”.
The process of regularization is to scale each sample to the unit norm （ The norm of each sample is 1）, If we want to calculate the similarity between two samples later, such as dot product or other kernel methods （ Like cosine similarity ）, This method will be very useful .
$$pFanCount：||X|{|}^p=(|x1{|}^p+|x2{|}^p+...+|xn{|}^p{)}^{1/p}$$
$$more\; thanstringphaselikedegree：sim(x_1,x_2)=\frac{x_1\cdot x_2}{||x_1||\cdot ||x_2||}$$

Data cleaning

Missing data

Noise data

• Identify the noise and remove it , Such as outlier identification ;
• Use other non noise data to smooth it , Such as data distribution .

Data inconsistency

Feature selection and feature extraction

feature selection

Feature selection mainly includes Two purposes ：

• Reduce the number of features 、 Dimension reduction , Make model generalization more powerful , Reduce overfitting ;
• Enhance understanding between features and eigenvalues .

Feature selection can be divided into filter、wrapper、embedded There are three types of methods ：

• Filter： Filtration method , according to Divergence perhaps The correlation Analyze each feature score , Set the threshold or the number of thresholds to be selected , Select features .
• Wrapper： Packaging method , according to Objective function （ It's usually a prediction score ）, Select several features at a time , Or exclude some features .
• Embedded： Embedding method , First use Some machine learning algorithms Train with the model , Get the weight coefficient of each feature , Select features from large to small coefficients . Be similar to Filter Method , But it's training that determines the quality of a feature .

Correlation coefficient method
Calculate the correlation coefficient between independent variable and dependent variable , When the correlation coefficient is less than the threshold, the variable is discarded .

Chi square test
This method is used when the independent variable and dependent variable are classified variables , It is used to test whether there is significant correlation between independent variables and dependent variables . The specific method of chi square test is shown in “ Box splitting method - Chi square test ”.

Relief Algorithm
Relief The algorithm is a feature weight algorithm (Feature weighting algorithms), According to the characteristics and categories The correlation Give different weights to features , Features with weights less than a certain threshold will be removed .
Relief The correlation between features and categories in the algorithm is based on Distinguishing ability of features to close samples .
The main steps are as follows ：

1. Initialize all feature weights $w_i=0$, Numerical attribute normalization ;
2. From the training set D Select a sample at random R, Then from and R similar Find the nearest neighbor sample in the sample of H, be called Near Hit, From and R Different types Find the nearest neighbor sample in the sample of M, be called NearMiss;
3. Update the weight of each feature ： If R and Near Hit In a certain feature A The distance on the is less than R and Near Miss Distance on the road , It shows that this feature is beneficial to distinguish the nearest neighbors of the same kind and different kinds , Then increase the weight of the feature ; conversely , Then reduce the weight of the feature ;
   $$w_i=w_i-d(R.A,H.A)+d(R.A,M.A)$$
   
4. Repeat the above process m Time , Finally, the weight of each feature is obtained , Output features larger than the threshold .

example ：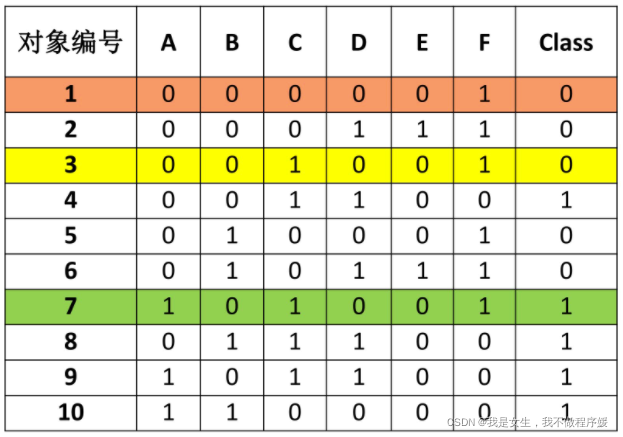

Relief The running time of the algorithm varies with the number of samples m And the number of original features N The increase of increases linearly , Therefore, the operation efficiency is very high .

feature extraction

PCA Algorithm
By modifying the original variables linear transformation , Extract new variables that reflect the essence of things , Remove redundancy at the same time 、 Reduce noise , achieve Dimension reduction Purpose .

1. Given data set , contain n Objects ,m Attributes ;
2. Centralization Data sets ： Subtract the attribute mean from each attribute value , The average value of the centralized data is 0, use $x_{n\times m}$ Express ;
3. Calculate the covariance matrix C, Elements $c_{ij}$ Attribute $A_i$ and $A_j$ The covariance between ：$c_{ij}={\sum }_{k=1}^n(x_{ki}-\overline{A_i)}(x_{kj}-\overline{A_j})$;
4. Calculate the characteristic root and characteristic equation of covariance matrix , The characteristic roots are arranged in descending order as ${\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_m\ge 0$, be ${\lambda }_1$ The corresponding eigenvector is the first principal component ,${\lambda }_2$ The corresponding eigenvector is the second principal component , The first i The contribution rate of the principal components is ：$\frac{{\lambda }_i}{{\sum }_{k=1}^m{\lambda }_k}$;
5. Leave the q The largest eigenvalues and their corresponding eigenvectors , Construct the principal component matrix P, Its first i Column vector $p_i$ It's No i A principal component （ That is, the eigenvector ）;
6. Calculate the reduced dimension matrix $Y_{n\times q}=X_{n\times m}{P}_{m\times q},q<n$.
   The new feature is a linear combination of the original feature .