Feature scaling for machine learning

The reason for data normalization

As shown in the figure below ：

The distance between samples is dominated by the time of discovery . This will make the data inaccurate , So our solution is to map all the data to the same size , Next we introduce two methods .

Maximum normalization （normalization)

Definition ： Map all data to 0-1 Between .

notes ： It is applicable to the case where the distribution has obvious boundary , But by outlier Greater impact .
Code ：

import numpy as np
import matplotlib.pyplot as plt
X = np.random.randint(0, 100, (50, 2))
X = np.array(X, dtype = float)
X[:,0] = (X[:,0] - np.min(X[:,0])) / (np.max(X[:,0]) - np.min(X[:,0]))
X[:,1] = (X[:,1] - np.min(X[:,1])) / (np.max(X[:,1]) - np.min(X[:,1]))

notes ： because numpy Only one data type can exist , So we need to convert the data type to float, Otherwise, the normalized data cannot be displayed correctly .

Then we plot the normalized data ：

plt.scatter(X[:,0], X[:,1])
plt.show()

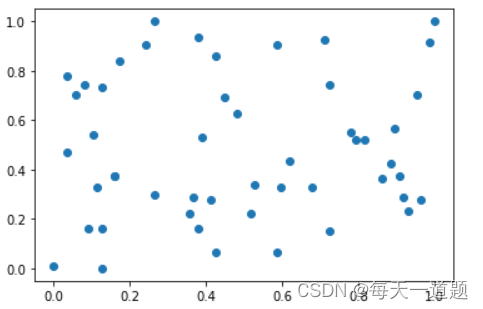
It is obvious that all the data are in 0-1 Between .

The mean variance is normalized （standardization）

Definition ： Put all the data together and put it on the average 0 The variance of 1 The distribution of

Applicable conditions ： The data distribution has no obvious boundary ; There may be extreme data values .
Code ：

X2 = np.random.randint(0, 100, (50, 2))
X2 = np.array(X, dtype = float)
X2[:,0] = (X2[:,0] - np.mean(X2[:,0])) / np.std(X2[:,0])
X2[:,1] = (X2[:,1] - np.mean(X2[:,1])) / np.std(X2[:,1])

Then we can draw ：

plt.scatter(X2[:,0],X2[:,1])
plt.show()

It can be seen that the data is not 0-1 Between .
Next, let's look at his mean and standard deviation ：

It is clear that the mean value is almost equal to 0, And the standard deviation is 1.