当前位置:网站首页>LeetCode+ 21 - 25
LeetCode+ 21 - 25
2022-06-10 23:29:00 【Sauerkraut】
Merge two ordered lists
Algorithm tags : recursive 、 Linked list 、 Merge two ways


Give two linked lists in ascending order , To merge it into an ascending linked list , Classical two-way merging algorithm
Look at the first number of the remaining numbers in the two linked lists each time , The first two pointers point to the beginning of the two linked lists
Compare the size of the element pointed to by two pointers at a time , Take the smaller one to the last position of the new linked list , The new linked list is empty at first
In the title sample , At first, the two linked lists point to the same number , Just take one of them , You can put the first node of the first linked list into the new linked list , Delete the first node , Then point the pointer of the first linked list to the next point , Next time, let's see which of the two pointers points to is smaller , Obviously the second pointer points to a smaller number , Put the first node of the second linked list into the new linked list , Then point the pointer to the next position , And so on
Special judgment header node is required / Possible changes in the header node , A virtual head node can be established to avoid special judgment , Use two pointers to point to the first node of the two linked lists respectively , Put two smaller ones at a time , Spell it at the back of the new linked list , Then move the pointer back one bit
Let's simulate the process




When a linked list is empty , Just splice another linked list to the end of the new linked list
Why is this correct ?
Find the minimum value of all remaining numbers each time and put it at the end of the new sequence , Because both sequences are ordered , Therefore, the first number remaining in each sequence must be the minimum value of the sequence , The first number of the first sequence is the minimum of the first sequence , The first number of the second sequence is the minimum of the second sequence , The minimum of these two numbers is the minimum of the whole sequence , Each time you take the smallest of the two pointers, it is the minimum value of all the remaining numbers
Algorithm problems generally do not consider memory problems , If considered , Just delete the virtual head node
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
// Create a virtual header node Define a variable to point to the tail node of the virtual head node Because each time we need to add... At the end of the new node You need to know who the tail node of the new linked list is
auto dummy = new ListNode(-1),tail = dummy;
// Traversing two linked lists
while(list1 && list2) {
// When both linked lists are not empty , Each time compare two linked lists which is smaller
if(list1->val < list2->val) {
//1. If the value of the first linked list is smaller , Just put list1 The value of the pointer is connected to the back of the new linked list 2. Update the tail node of the new linked list to list1
tail = tail->next = list1;
// The first linked list uses a dot The pointer of the first linked list moves back one bit
list1 = list1->next;
} else {
//list2 Empathy
tail = tail->next = list2;
list2 = list2->next;
}
}
// After the loop ends, there may be a non empty linked list If list1 Not empty list1 Receive the last , If list2 Not empty lsit2 Receive the last
if(list1) tail->next = list1;
if(list2) tail->next = list2;
return dummy->next;
}
};Bracket generation
Algorithm tags : character string 、 Dynamic programming 、 to flash back 、 recursive

give n A left bracket and n Right parenthesis , The scheme of outputting all legal parenthesis sequences , The legal scheme means that the brackets can be perfectly matched
Here are the legal and illegal cases

Yes n A left bracket and n Right parenthesis , When judging , As long as every left bracket can have a right bracket corresponding to it
Refer to the first 15 topic :
To judge whether a sequence of parentheses is legal, use the stack to judge , If you encounter an open parenthesis, push it onto the stack , If a right bracket is encountered, judge whether it matches the left bracket at the top of the stack , If it matches, sift it out
Because this topic has only ' ) ' and ' ( ', The top element of the stack must be an open parenthesis , The current element must be a closing parenthesis , It must match . It can be found that this question does not need to judge whether it matches , Just make sure that when we When you encounter each right parenthesis , There must be an open bracket in the stack
n A left bracket and n Under what circumstances is a closing parenthesis , The constructed sequence is legal ?
Draw the following conclusion

Because the left and right parentheses given by the title are n individual , So the second condition must be satisfied , When generating a sequence , As long as the first condition is met
As long as any prefix is satisfied ' ( ' Must be greater than or equal to ' ) ' Quantity is enough , When we come across a closing parenthesis , There must be an open bracket in the stack to match it
expand :
If it is not required to output all schemes , Only the number of legal bracket sequences is required to be output , This number is the Cartland number

How to output all schemes ?
dfs Recursively output all schemes , A recursive search tree can be used to consider
You can think about it one by one , Altogether 2n position , Think back and forth , Let's assume that some situations have been considered , Consider what the next person can fill in each time : Or fill in the left bracket , Or fill in the right parenthesis
Next, let's see what we can do to fill in the left bracket ? In any case, you can fill in the right bracket ?
You can find that you can fill in the left parenthesis in any case , As long as the number of left parentheses is less than n You can fill in the left bracket
Attention should be paid to filling in the right bracket , The number of right parentheses should be less than n,( Any prefix must meet the following requirements ' ( ' Must be greater than or equal to ' ) ' Number )
If you want to fill in the closing bracket , The number of left parentheses must be strictly greater than the number of right parentheses , If it's equal , Fill in the closing parentheses , There are more right parentheses in the prefix
stay dfs When , Consider two situations at a time , As long as the first condition is met , You can fill in the left parenthesis and recurse , As long as the second condition is met , You can fill in the right parenthesis and recurse
The time complexity of the whole algorithm is the number of schemes , That is to say, the number of Cartland , As the final solution needs to be inserted into vector in , Finally, you need to multiply by one 2n( Each scheme seq Is the length of the 2n)
These two corollaries apply only to a class of parentheses


class Solution {
public:
// Define an array to record answers
vector<string> ans;
vector<string> generateParenthesis(int n) {
// At first, the left and right parentheses are 0 seq It's empty
dfs(n,0,0,"");
return ans;
}
// The number of brackets n The current sequence of parentheses seq
void dfs(int n,int lc, int rc,string seq) {
// When the left and right parentheses are used up Add answers seq
if(lc == n && rc == n) ans.push_back(seq);
else {
// Judge whether the left bracket can be added
if(lc < n) dfs(n,lc + 1,rc,seq + '(');
// Judge whether the closing bracket can be added
if(rc < n && lc > rc) dfs(n,lc,rc + 1,seq + ')');
}
}
};Merge K An ascending list
Algorithm tags : Linked list 、 Divide and conquer 、 Pile up ( Priority queue )、 Merge sort


Refer to the first 21 topic , Merge two ways : Two sequences are given , Two pointers to the beginning of two sequences , Each time, take the smaller number of two pointers to the next position of the new sequence

If there is k The sequences are actually similar , Suppose there is 4 A sequence of , use 4 A pointer points to 4 A sequence of , Every time 4 Take out the smallest one of the three pointers and put it at the end of the new sequence

because 4 All sequences are in ascending order , The number pointed to by the first pointer is the minimum value of the first sequence , The number pointed to by the second pointer is the minimum value of the second sequence , And so on , The number pointed to by the third pointer is the minimum value in the third sequence , therefore , this 4 The minimum value of a pointer is this 4 The minimum value of a sequence
How can I k Take the minimum value from the pointer ?
You can use a loop to find the minimum , Suppose the total length of all linked lists is n, Time complexity is n × k, Every time you add a new element, you loop k Time , Time complexity is O( n × k )
You can maintain this with a heap k A pointer to the , Each time the minimum value is found, the operation is O( 1 ), After finding the minimum value , Move the minimum pointer back one bit , Then insert it into the new linked list , The time complexity of this step is O( logn ), It can be used stl The priority queue inside , You need to pass in a custom comparison function , and sort The incoming comparison function is different
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
// The comparison function of the priority queue does not pass a function but a structure type Need to overload parentheses
struct Cmp {
// By default, the priority queue is a large root heap, which will put a large number in front of it But we want to put small numbers first By default '<' Change to '>' that will do
bool operator() (ListNode* a,ListNode* b) {
return a->val > b->val;
}
};
ListNode* mergeKLists(vector<ListNode*>& lists) {
// Define a heap / The priority queue stores pointers If the user-defined comparison function is not passed in, it will compare by address Actually, we need to compare according to the value of the pointer
priority_queue<ListNode*,vector<ListNode*>,Cmp> heap;
// Define a virtual header node Define a variable to point to the tail node of the virtual head node Because each time we need to add... At the end of the new node You need to know who the tail node of the new linked list is
auto dummy = new ListNode(-1),tail = dummy;
// Put this first k Insert the header node of a linked list into the heap If it is not empty, insert the node Note that the address of the head node of each linked list push Went in. , Instead of putting the whole list push go in
for(auto l : lists) if(l) heap.push(l);
//k Road merging When there are elements in the heap , Find the minimum value every time
while(heap.size()) {
// Every time you take out the top element
auto t = heap.top();
// Then delete the top element of the heap
heap.pop();
// Insert the current node after the tail node After inserting ,t Change to a new tail node and update the tail node
tail = tail->next = t;
// If t There is the next node , Just insert the next node into the heap It is equivalent to moving the pointer back one bit
if(t->next) heap.push(t->next);
}
return dummy->next;
}
};Why overloaded parentheses ?
because STL The container uses the parenthesis operator of the structure when comparing
greater<int>() and less<int>() Use _chijianxingfeng The blog of -CSDN Blog _less<int>()
When comparing two elements, the container will call Cmp(a,b), Will return a bool value , If a Should be in b In front of , Returns the true, Otherwise it will return to false, Overloaded parentheses when implementing the comparison function , When called, it will return as required
If a Less than b It'll be in the front , If a Greater than b It'll be in the back
It is normal to write less than , It's a big pile , Hope to use small root pile , Just change less than to greater than
Two or two exchange nodes in a linked list
Algorithm tags : recursive 、 Linked list


Give us a linked list , You need to swap all its adjacent elements , Return the value after exchange , Be careful : You cannot modify the values in each node , Only the structure can be changed
Exchange before
![]()
After exchanging
![]()
If there is 5 Elements , The last element doesn't matter , The results are as follows

First, you can find that the head node of the original linked list will change , You need to create a virtual head node , There is no need to consider the problem that the head node will change

Each enumeration should enumerate two adjacent nodes
The two pointers point to the first point of the original linked list and the next point of the first point

Because the head node will change , First, create a virtual head node

Need to swap 1 and 2 These two nodes , Hope it becomes 2 and 1

Next, let's take a look at the specific operation ?
First, you need an additional pointer to the virtual head node

① The virtual head node's next Pointer to 2

② take 2 Of next Change the pointer to point to 1

③ take 1 Of next Change the pointer to point to 3

④ Point the pointer to the virtual head node to 1

⑤ The elements to be exchanged in the next step are 1→next and 1→next→next, The first step will be 1 Of next Change the pointer to point to 4, The second step will be 4 Of next Change the pointer to point to 3, The first 3 Step by step 3 Of next Change the pointer to null

When enumerating , Each time the pointer points to the previous position of the two adjacent elements to be exchanged , If you want to exchange 1 and 2, The pointer should point to 1 The front position , Want to swap 3 and 4, The pointer should point to 3 The front position
Order of attention : After the exchange , If you change first 2 Words ,2 Of next The pointer 3 I can't find


/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
// Create a virtual header node Let the virtual head node next The pointer points to the real header node
auto dummy = new ListNode(-1);
dummy->next = head;
// Traversing from front to back p Is the point before the exchange of two points
for(auto p = dummy;p->next && p->next->next/* The operation is required only when two points exist */;) {
// First find the first point to exchange Find the second point to exchange
auto a = p->next,b = a->next;
// take p->next from a Change to point b
p->next = b;
// take a->next Change to point b->next
a->next = b-> next;
// then b->next Change to point a
b->next = a;
// then p Point to a
p = a;
}
return dummy->next;
}
};K A set of flip list
Algorithm tags : recursive 、 Linked list


![]()
similar 24 topic , Give a list , Swap two adjacent elements and flip them k Elements , If the last remaining number is not enough k Then they keep the original order
A sample of
The original list is 1、2、3、4、5,k = 3, Before turning over 3 Elements , The last two elements are insufficient 3 Just keep the original order
Because the head node may change , For convenience, you can create a virtual head node first , Avoid special judgment header nodes

Make a pointer that needs to be exchanged each time k The previous element of an element , Each time, you need to judge whether there is... After this element k Elements : Just go through it directly , If not enough k individual , direct break, If enough k You need to exchange this k Elements

In exchange for 1、2、3 Needs to be divided into 3 There are three parts to consider
① take 1、2、3 The inner side is reversed
First the 1 and 2 The reverse becomes 2 and 1, then 2 and 3 The reverse becomes 3 and 2


② Point the front connected part to the correct position

③ Point the connecting part at the right position

Let's take a look at how to implement the above steps
Flip the internal nodes : Point to the first element with a pointer , The second pointer points to the second element

Point to two adjacent elements with two pointers at a time , Change the second pointer from pointing to the next element to pointing to the previous element

Then the two pointers are reversed by one digit , Repeat the above steps

details
If you change the pointer that the second pointer points to to the previous one , After a change , The next element is missing , You need to store the next element first
Just two pointers will repeat k - 1 Time , Finally arrive at 3 and 4 The location of

Let the virtual head node point to the first pointer just traversed 3, Let the virtual head node next The pointer 1 Point to the second pointer just traversed 4

After that , Give Way p Point to the previous element of the next group c

Each of these elements will only traverse the constant times , The time complexity is linear , Two for loop , A traversal n Time , Total traversal 2n Time , The time complexity is O( 2n )
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
// Define a virtual header node
auto dummy = new ListNode(-1);
dummy->next = head;
// Start from the virtual head node to traverse the entire linked list Go through it first p Is the back enough k Elements
for(auto p = dummy;;) {
// Jump back k Step
auto q = p;
// from p Start jumping back k Whether the step element is empty or not Every time q Jump back
for(int i = 0;i < k && q/* Need assurance q Not an empty node */;i++) q = q->next;
// If jump k Blank after step indicates insufficient k Bit elements , If it is not empty, it means that at least k Bit elements
if(!q) break;
// First define two nodes In limine ,a Point to the first element of each group ,b Point to a Next element of
auto a = p ->next,b = a->next;
// A total of k - 1 Two adjacent locations
for(int i = 0;i < k - 1/* A total of k - 1 side */;i++ ) {
// Need first b Of next The pointer is stored
auto c = b->next;
// Give Way b->next Point to a
b->next = a;
// Give Way a Jump to the b The location of , Give Way b Jump to the c The location of
a = b,b = c;
}
// The above k The edges inside the nodes are reversed
// Storage c
auto c = p->next;
// Give Way p Of next Pointer to a, Give Way c Of next Pointer to b
p->next = a,c->next = b;
// Finally let p Jump to the c The location of
p = c;
}
// Return to the next position of the virtual head node That is, the new header node
return dummy->next;
}
};边栏推荐
- Sealem Finance-基于Web3的全新去中心化金融平台
- Creation of thread pool
- Optimize code to remove if else
- [Interface tutorial] how does easycvr set platform cascading through the interface?
- Ride the storm and explore the secret behind the open source of flyfish, a data visualization development platform!
- 使用TSA包中的 beersales 数据集建立TAR模型
- 300 questions on behalf of the first lecture on determinant
- Data and information resource sharing platform (IV)
- 线程池的创建
- 联想首次详解混合云Lenovo xCloud五大优势,如何打造智能化数字底座
猜你喜欢

Design language testing for functional testing: what tests are included in functional testing? What is the role of each
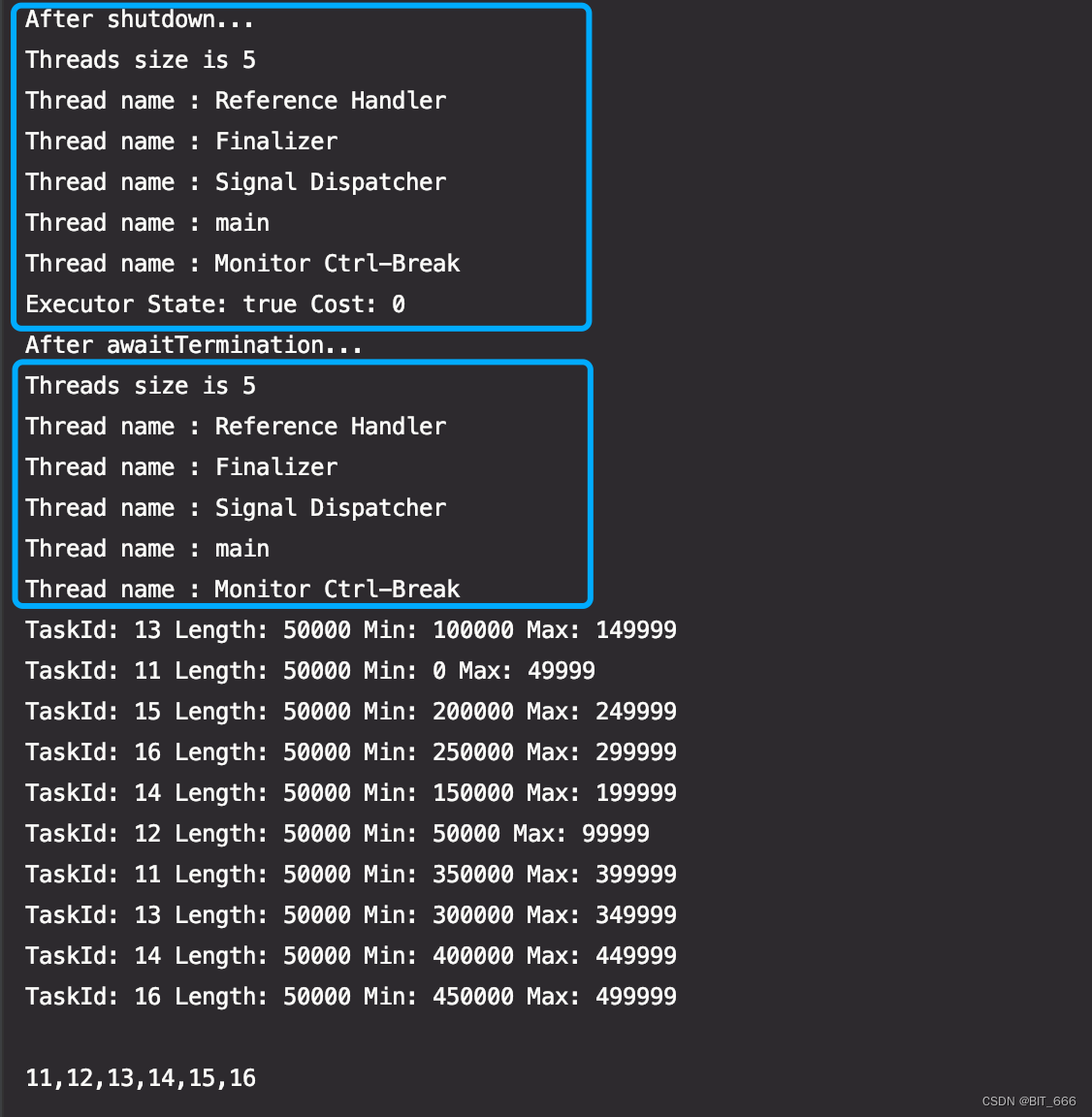
Exécuteur - shutdown, shutdown Now, awaittermination details and actual Fighting

Dell R730 raid5 安装Server 2016(解决磁盘大于2T)

The time (in minutes) required for a group of workers to cooperate to complete the assembly process of a part are as follows:

34. find the first and last positions of elements in the sorted array - binary search, double pointer

Why is the kotlin language not popular now?

已知某种木材的横纹抗压力服从N(x,d2),现对十个试件作横纹抗压力试验,得数据如下:(单位:kg/cm2)

Introduction to software testing: the concept and process of software testing (brilliant content)

PwnTheBox,Web:hello

200 c language words, please collect!
随机推荐
爬虫学习知识
Data file nc6oa Txt consists of 6830 gene expression data from 33 cancer cell lines, each of which is a type of cancer cell. Please cluster the 33 cell lines according to the gene expression data (the
MySQL table mechanism
【视频】KMEANS均值聚类和层次聚类:R语言分析生活幸福指数可视化|数据分享
1.打开R程序,使用 apply 函数计算1到12按先后次序每隔3个数一组的和。即,计算1+4+7+10=?2+5+8+11=?,3+6+9+12=?
PwnTheBox,Pwn:tutorial1
Wireshark抓取rtp负载ts流介绍(UDP组播)
Basic SQL statement - insert
[flutter problem series Chapter 6] how to achieve the scrolling effect of list messages in flutter
【sql语句基础】——增(insert)
Dell r730 RAID5 installation server 2016 (disk larger than 2t)
功能测试之设计语言测试:功能测试包含哪些测试?分别有什么作用
Kotlin语言现在怎么不火了?
数据与信息资源共享平台(四)
OpenVP*整合ldap認證
Executor - Shutdown、ShutdownNow、awaitTermination 詳解與實戰
Solutions to the error reported by executing Oracle SQL statement [ora-00904: "createtime": invalid identifier] and [ora-00913: too many values]
Redis list list common commands
leetcode 130. Surrounded Regions 被围绕的区域(中等)
C语言创建动态二维数组