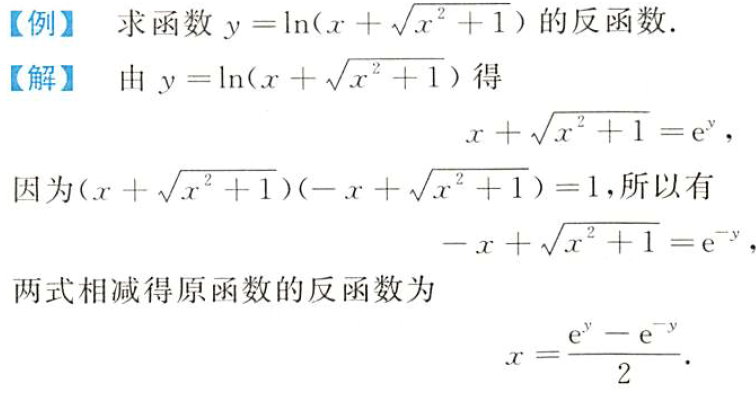当前位置:网站首页>math_数学表达式&等式方程的变形&组合操作技巧/手段积累
math_数学表达式&等式方程的变形&组合操作技巧/手段积累
2022-06-29 09:59:00 【xuchaoxin1375】
数学表达式&等式方程的变形&组合操作技巧/手段积累
分式
分子分母同时乘以&除以同一个表达式
- 分子有理化
- 分母有理化
分式拆分(因子重组)
方程(等式)
方程
数学中,方程(equation)可以简单的理解为含有未知数的等式,
- 即含有一个以上的未知数并结合等号的数学公式(formula)
等式
在数学的领域中,若两个数学对象在各个方面都相同,则称他们是相等的。这就定义了一个二元谓词等于,写作
x = y {\displaystyle x=y} x=y
当且仅当x和y相等。通常意义上,等于是通过两个元素间的等价关系来构造的。
将两个表达式用等于符号连起来,就构成了等式,
注意,有些时候
A = B {\displaystyle A=B} A=B
并不表示等式。例如,
T ( n ) = O ( n 2 ) {\displaystyle T(n)=O(n^{2})} T(n)=O(n2)
表示在数量级
n 2 {\displaystyle n^{2}} n2
因为这里的符号=不满足当且仅当的定义,所以它不等于等于符号;实际上,
O ( n 2 ) = T ( n ) {\displaystyle O(n^{2})=T(n)} O(n2)=T(n)
是没有意义的。请参见大O符号了解这部分内容。
常见手法
错位相减
等式两边同时做相同的处理
- 1的代换(譬如
- 三角函数: 1 = s i n 2 x + c o s 2 x 1=sin^2x+cos^2x 1=sin2x+cos2x
- 幂: ( x + x 2 + 1 ) ( − x + x 2 + 1 ) = 1 (x+\sqrt{x^2+1})(-x+\sqrt{x^2+1})=1 (x+x2+1)(−x+x2+1)=1
- 同时乘方
- 同时加上某一个表达式
- 带入消元(减小变量个数)
- 等式组加减消元
- 譬如,函数的最值相关问题
- 1的代换(譬如
一般表达式处理
表达式(expression)此处是数学表达式(mathematical expression)的简称,
列项相消
譬如一部分的数列求和
- ∑ i = 1 n 1 ( i ) ( i + 1 ) = ∑ i = 1 n 1 ( i ) − 1 ( i + 1 ) = ∑ i = 1 n 1 i − ∑ i = 1 n 1 i + 1 = ( 1 1 + ∑ i = 2 n 1 i ) − ( ∑ i = 2 n 1 i + 1 n + 1 ) = 1 − 1 1 + n 令 : { f ( i ) = 1 i ; 则 g ( i ) = f ( i + 1 ) ‾ = 1 i + 1 , 可 见 是 一 个 ( 离 散 ) 函 数 的 向 左 偏 移 1 \sum\limits_{i=1}^n{\frac{1}{(i)(i+1)}} =\sum\limits_{i=1}^n{\frac{1}{(i)}-\frac{1}{(i+1)}} =\sum\limits_{i=1}^n{\frac{1}{i}} -\sum\limits_{i=1}^{n}\frac{1}{i+1} \\=(\frac{1}{1}+\sum\limits_{i=2}^{n}{\frac{1}{i}}) -(\sum\limits_{i=2}^{n}\frac{1}{i}+\frac{1}{n+1}) \\=1-\frac{1}{1+n} \\ 令:\begin{cases} f(i)=\frac{1}{i}; \\则g(i)=\underline{f(i+1)}=\frac{1}{i+1},可见是一个(离散)函数的向左偏移1 \end{cases} i=1∑n(i)(i+1)1=i=1∑n(i)1−(i+1)1=i=1∑ni1−i=1∑ni+11=(11+i=2∑ni1)−(i=2∑ni1+n+11)=1−1+n1令:{ f(i)=i1;则g(i)=f(i+1)=i+11,可见是一个(离散)函数的向左偏移1
对数&指数的转化
换元法
配凑法
加上一个表达式再减去相同大小的表达式
例如,分离常数:(可以起到集中变量x的效果)
- f ( x ) = 2 x − 1 x + 1 = 2 x − 1 + 2 − 2 1 2 ( 2 x + 2 ) = 2 x + 2 − 3 x + 1 = 2 + − 3 x + 1 f(x)=\frac{2x-1}{x+1}=\frac{2x-1+2-2}{\frac{1}{2}(2x+2)} =\frac{2x+2-3}{x+1}=2+\frac{-3}{x+1} f(x)=x+12x−1=21(2x+2)2x−1+2−2=x+12x+2−3=2+x+1−3
再比如导函数求导法则种的乘法求导法则的推导/证明:
- f ( x ) = u ( x ) v ( x ) f ′ ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x = lim Δ x → 0 u ( x + Δ x ) v ( x + Δ x ) − u ( x ) v ( x ) Δ x = lim Δ x → 0 u ( x + Δ x ) v ( x + Δ x ) − u ( x ) v ( x ) + u ( x ) v ( x + Δ x ) − u ( x ) v ( x + Δ x ) Δ x 配 凑 & 组 合 = lim Δ x → 0 [ ( u ( x + Δ x ) − u ( x ) ) v ( x + Δ x ) ] + [ u ( x ) ( v ( x + Δ x ) − v ( x ) ) ] Δ x = lim Δ x → 0 { ( u ( x + Δ x ) − u ( x ) ) Δ x ⋅ v ( x + Δ x ) + u ( x ) ⋅ ( v ( x + Δ x ) − v ( x ) ) Δ x } = lim Δ x → 0 ( u ( x + Δ x ) − u ( x ) ) Δ x ⋅ v ( x + Δ x ) + lim Δ x → 0 u ( x ) ⋅ ( v ( x + Δ x ) − v ( x ) ) Δ x = lim Δ x → 0 ( u ( x + Δ x ) − u ( x ) ) Δ x lim Δ x → 0 v ( x + Δ x ) + lim Δ x → 0 u ( x ) lim Δ x → 0 ( v ( x + Δ x ) − v ( x ) ) Δ x = u ′ ( x ) v ( x ) + u ( x ) v ′ ( x ) f(x)=u(x)v(x) \\ f'(x)=\lim_{\Delta x\rightarrow 0} {\frac{f(x+\Delta x)-f(x)}{\Delta x}} \\=\lim_{\Delta x\rightarrow 0} \frac{ {u(x+\Delta x)v(x+\Delta x)-u(x)v(x)}}{\Delta x} \\=\lim_{\Delta x\rightarrow 0} \frac{ {u(x+\Delta x)v(x+\Delta x)-u(x)v(x) +u(x)v(x+\Delta x)-u(x)v(x+\Delta x)}} {\Delta x} \\配凑\&组合 \\ =\lim_{\Delta x\rightarrow 0} \frac{[(u(x+\Delta x)-u(x))v(x+\Delta x)] +[u(x)(v(x+\Delta x)-v(x))]} {\Delta x} \\=\lim\limits{\Delta x\rightarrow 0} \left \{ {\frac{(u(x+\Delta x)-u(x))}{\Delta x}\cdot v(x+\Delta x) +u(x)\cdot \frac{(v(x+\Delta x)-v(x))}{\Delta x}} \right \} \\=\lim_{\Delta x\rightarrow0} {\frac{(u(x+\Delta x)-u(x))}{\Delta x}\cdot v(x+\Delta x)} +\lim_{\Delta x\rightarrow0}u(x)\cdot \frac{(v(x+\Delta x)-v(x))}{\Delta x} \\=\lim_{\Delta x\rightarrow0} {\frac{(u(x+\Delta x)-u(x))}{\Delta x}\lim_{\Delta x\rightarrow0} v(x+\Delta x)} \\ +\lim_{\Delta x\rightarrow0}u(x)\lim_{\Delta x\rightarrow0} \frac{(v(x+\Delta x)-v(x))}{\Delta x} \\=u'(x)v(x)+u(x)v'(x) f(x)=u(x)v(x)f′(x)=Δx→0limΔxf(x+Δx)−f(x)=Δx→0limΔxu(x+Δx)v(x+Δx)−u(x)v(x)=Δx→0limΔxu(x+Δx)v(x+Δx)−u(x)v(x)+u(x)v(x+Δx)−u(x)v(x+Δx)配凑&组合=Δx→0limΔx[(u(x+Δx)−u(x))v(x+Δx)]+[u(x)(v(x+Δx)−v(x))]=limΔx→0{ Δx(u(x+Δx)−u(x))⋅v(x+Δx)+u(x)⋅Δx(v(x+Δx)−v(x))}=Δx→0limΔx(u(x+Δx)−u(x))⋅v(x+Δx)+Δx→0limu(x)⋅Δx(v(x+Δx)−v(x))=Δx→0limΔx(u(x+Δx)−u(x))Δx→0limv(x+Δx)+Δx→0limu(x)Δx→0limΔx(v(x+Δx)−v(x))=u′(x)v(x)+u(x)v′(x)
拆项相消
方程组成组处理(经常是相加/减)法
很多和1有关
直观的例子
- 这里的
元可能是指复杂的式子(作为整体)
边栏推荐
- Numeric Keypad
- BUUCTF RE-easyre
- JS post download file
- 在 2022 年找工作,毕业生们的 “最后一课”
- UserWarning: Usage of dash-separated ‘script-dir‘ will not be supported in future versions. 笔记
- Qt编写物联网管理平台37-逻辑设计
- Ningde era Kirin battery has greater ambition
- 【NLP】文本生成专题1:基础知识
- Software test model (V model and W model)
- Here comes the tutorial of datawhale recommendation system!
猜你喜欢

世界上第一个“半机械人”去世,改造自己只为“逆天改命”

SQL Server 数据库的统计查询

ssh密钥泄露(B模块赛题)——应用服务漏洞扫描与利用

免费送书啦!畅销书《 OpenCV图像处理入门与实践》一本全搞定

这个mySQL安装的时候怎么搞去了?

美国EB-5移民再现利好,区域中心再授权政策被叫停

The encryption market has exploded one after another. Can Celsius avoid bankruptcy?

任职 22 年,PowerShell 之父将从微软离职:曾因开发 PowerShell 被微软降级过

如何优雅的写 Controller 层代码?

Bug description, rating and life cycle
随机推荐
MySQL查询时如何找出错误格式的手机号
在 2022 年找工作,毕业生们的 “最后一课”
【Rust每周一库】Tokei - 统计代码行数等信息的实用工具
Summary after reading how to read a Book
历史上的今天:马斯克出生;微软推出 Office 365;蔡氏电路的发明者出生
Dropout layer
USB转RS485串口电路设计「建议收藏」
(JS)模仿indexOf方法寻找字符串中某个字符的位置
The product strength is not inferior to that of BYD. Geely Dihao l Raytheon hi · x delivered 10000 units in the first month
Redis installation and cluster setup under Linux
世界上第一个“半机械人”去世,改造自己只为“逆天改命”
有人遇到FlinkCdc同步MySQL时候出现的这个问题吗?
【C语言进阶】通讯录实现
如何优雅的写 Controller 层代码?
Daily question brushing record (VII)
dropout层
Numeric Keypad
SQL Server 数据库的几种简单查询
VI exit exit VIM applicable novice
Numeric Keypad