[dynamic planning] - Digital triangle

---

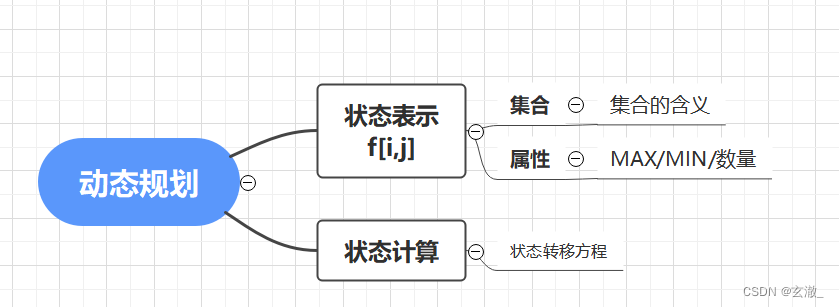
Dynamic programming

The dynamic programming algorithm regards the original algorithm as a progressive process of several overlapping subproblems , The solving process of each subproblem constitutes a “ Stage ”. After the calculation of the previous stage , Dynamic planning will perform the calculation of the next stage .

In order to ensure that these calculations can be done in sequence 、 Without repetition , Dynamic programming requires that the solved subproblems are not affected by the subsequent stages . This condition is also called “ No aftereffect ”. In other words , Dynamic programming traverses the state space to form a directed acyclic graph , Ergodic order is a topological order of the directed acyclic graph . In the node correspondence problem of ordered acyclic graphs “ state ”, The edges in the graph are between the corresponding states “ Transfer ”, The selection of transfer is the of dynamic programming “ Decision making ”.

In many cases , Dynamic programming is used to solve optimization problems . here , The optimal solution of the next stage should be obtained from the optimal solution of the subproblems in the previous stages . This condition is called “ Optimal substructural properties ”.

“ state ”、“ Stage ” and “ Decision making ” It is the three elements of the dynamic programming algorithm , and “ The overlapping of subproblems ”,“ No aftereffect ” and “ Optimal substructure ” It is the three basic conditions that the problem can be solved by dynamic programming .

The dynamic programming algorithm applies the same calculation process to the same kind of subproblem in each stage , It is like running a fixed formula on several input data with the same format . therefore , We usually just need to define DP Calculation process , You can program it , This calculation process is called “ State transition equation ”.

Yan style thinking

from aggregate Think about it from the perspective of ： 

---

Example ：AcWing 1015. Picking flowers

---

Collective meaning ： All from     Go to the     Of all routes Maximum  

In state calculation , Very important division basis ：“ Last ”

A collection of Basis of division ：1. Not heavy 2. No leakage （ Without repeating this point is , Double counting can occur , Because the last is to take the most value of the subset ）

---

AC Code  

#include <iostream>
#include <cstring>
using namespace std;

const int N = 110;

int n, m;
int w[N][N];
int f[N][N];

int main()
{
    int T; cin >> T;
    while(T -- )
    {
        scanf("%d%d", &n, &m);
        for(int i = 1; i <= n; i ++ )
            for(int j = 1; j <= m; j ++ ) 
                scanf("%d", &w[i][j]);
        
        for(int i = 1; i <= n; i ++ )
            for(int j = 1; j <= m; j ++ )
                f[i][j] = max(f[i][j - 1], f[i - 1][j]) + w[i][j];
        cout << f[n][m] << endl;
    }
    return 0;
}

---

Example ：AcWing 1018. Minimum tolls  

---

With the above Picking flowers Is a similar type of topic . More Time constraints （  ）.

This time limit Equivalent to Don't go back

Because what we want is minimum value , This problem needs to be solved Initialize the boundary .

---

AC Code

#include <iostream>
#include <cstring>
using namespace std;

const int N = 210, INF = 0x3f3f3f3f;

int n;
int w[N][N];
int f[N][N];


int main()
{
    cin >> n;
    
    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= n; j ++ )
            scanf("%d", &w[i][j]);
    
    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= n; j ++ )
            if(i == 1 && j == 1) f[i][j] = w[i][j];
            else 
            {
                f[i][j] = INF;
                if(i > 1) f[i][j] = min(f[i][j], f[i - 1][j] + w[i][j]);
                if(j > 1) f[i][j] = min(f[i][j], f[i][j - 1] + w[i][j]);
            }
            
    cout << f[n][n] << endl;        
    return 0;
} 

---

Example ：AcWing 1027. Take the number of squares

sample input ：

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

sample output ：

67

---

This question is compared with the previous two questions , More A total of two such restrictions . 

In the case of walking only once :

  It means   All from     Go to the     Of all routes Maximum  

In the case of walking twice :

  All from  ,  Go to the    The maximum value of all sets of paths of

How to deal with it “ The same grid cannot be selected repeatedly ”？

Only in    when , The grid of two paths will coincidence  

   Two people Go at the same time k Step （ Sum of horizontal and vertical coordinates ）（ It's like picking peanuts ）

  All from   ,   Go to    The maximum value of the path

---

AC Code  

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 15;

int n;
int w[N][N];
int f[N * 2][N][N];

int main()
{
    cin >> n;
    int a, b, c;
    while(cin >> a >> b >> c, a || b || c) w[a][b] = c;
    
    for(int k = 2; k <= n + n; k ++ )
        for(int i1 = 1; i1 <= n; i1 ++ )
            for(int i2 = 1; i2 <= n; i2 ++ )
            {
                int j1 = k - i1, j2 = k - i2;
                if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
                {
                    int t = w[i1][j1];
                    if(i1 != i2) t += w[i2][j2];
                    int &x = f[k][i1][i2];
                    x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1 - 1][i2] + t);
                    x = max(x, f[k - 1][i1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1][i2] + t);
                }
            }
    cout << f[n + n][n][n];
    return 0;
}

---