当前位置:网站首页>[cute new solution] Fibonacci sequence
[cute new solution] Fibonacci sequence
2022-07-27 13:09:00 【ASCE1885】
About me : WeChat official account : Interviewer asked , Original high-quality interview questions , Start with the interview question , But it's not just interview questions .【 Cute new problem solving 】 The series tries to From the perspective of newcomers To look at and solve problems , This question is to force deduction 509 topic Fibonacci number :https://leetcode.cn/problems/fibonacci-number/.
The first sight of the subject , I believe most people are like me , You can pass with your eyes closed recursive Write the following code :
class Solution {
public int fib(int N) {
if (N < 2) {
return N;
}
return fib(N-1) + fib(N-2);
}
}
The advantage of recursion is that the code is simple , It also conforms to the thinking of computer , After the code is submitted , As you can see, the results are as follows :

You can see , Because it's recursive , And there is A lot of double counting , Longer time consuming ; The time complexity of recursive algorithm is to multiply the number of subproblems by the time required to solve a subproblem , The recursion of Fibonacci sequence can be imagined as a binary tree , The nodes of the binary tree correspond to a recursive function ( for example fib(4)), The time complexity of the number of subproblems is O(2ᴺ), The time required to solve a sub problem is an addition time , for example fib(1) + fib(2) Time for , That is to say O(1), Therefore, the time complexity of the above recursive solution is O(2ᴺ).
One optimization method is through Memorandum Save the calculation results , Avoid double counting , For example, through Array or hash table Fine , As shown below , We use arrays as the implementation of memos :
class Solution {
public int fib(int N) {
if (N == 0) {
return 0;
}
// Initialize memo array , The array size is N+1, Because arrays are from 0 Start , What the title requires is fib(N) Value
int[] memo = new int[N+1];
return helper(memo, N);
}
/**
* Auxiliary function
*/
private int helper(int[] memo, int N) {
// base case
if (N == 1 || N == 2) {
return 1;
}
// Memo mode , Avoid double counting
if (memo[N] != 0) {
return memo[N];
}
// Recursively call , And save the return value into the memo array
memo[N] = helper(memo, N-1) + helper(memo, N-2);
return memo[N];
}
}
By introducing a memo , We avoid a lot of double counting , The number of subproblems is O(N), The time to solve a sub problem is still O(1), Therefore, the time complexity of the recursive solution of the memo above is O(N), The code executes as follows :

You can see , The implementation time has been greatly reduced , And because of the extra space memo Array , therefore , Memory consumption has increased , This is typical Space for time .
Okay , Here, in fact, the optimal solution of this problem has also been obtained , Because the time complexity is already O(N) 了 , No further reduction is possible . But if you have known about dynamic planning before , Because you know that , Fibonacci sequence problem can also be solved by dynamic programming . The general form of dynamic programming problem is to find the best value , For example, find the longest increasing subsequence , Minimum editing distance, etc , The Fibonacci series problem itself does not seek the maximum value , But because it can be used to demonstrate the idea of dynamic programming and problem-solving routines , Therefore, I like to mention The first question of dynamic programming The title of .
Before formally introducing the problem-solving routine of dynamic programming , Let's compare the Fibonacci sequence problem The difference between recursion and dynamic programming :
The recursive solution is The top-down Thought , for example , We are from a larger original problem , for example fib(10) Start , Break down the scale step by step ( If decomposed into fib(9) and fib(8) Two sub questions ), Then go back to the answer level by level , Finally get the original problem The dynamic programming solution is Bottom up Thought , for example , We start with the smallest problem , for example fib(1)、fib(2) Start to deduce upwards , Until get fib(10), therefore , Dynamic programming problems are generally Use loop iteration instead of recursion To do the calculation .
Reference code Capriccio , In this paper, the six steps of dynamic programming are as follows :
determine dp The meaning of arrays and subscripts (dp An array may be a one-dimensional array 、 Two dimensional array, etc ) Determine the recurrence formula dp How to initialize an array determine dp The traversal order of the array , May be forward traversal 、 Reverse traversal 、 Oblique traversal, etc Give an example to deduce dp Array , Through the dp The array prints out , And compare with the results calculated by your own brain , For debugging use Think about whether the state can be compressed , Further improve space efficiency
good , Apply the above solution steps to the Fibonacci sequence problem , The results are as follows :
determine dp The meaning of arrays and subscripts :dp[i] The meaning of is... In Fibonacci series i The value of the number Determine the recurrence formula : The title has been given , namely dp[n] = dp[n-1] + dp[n-2] dp How to initialize an array : The title has been given , namely dp[0]=0; dp[1]=1; determine dp The traversal order of the array : When you want to get dp[n] The value of is , First of all, we need to know dp[n-1] and dp[n-2] Value , therefore , We need to traverse the array from small to large Give an example to deduce dp Array : It can be used when debugging is required Think about whether the state can be compressed : If you can't think clearly now , We can think about it after we finish writing the above code
The final dynamic programming solution code is as follows :
class Solution {
public int fib(int N) {
if (N == 0) {
return 0;
}
// Definition dp Array
int[] dp = new int[N+1];
// determine dp The initialization state of the array
dp[0] = 0;
dp[1] = 1;
// Loop iteration ,dp Array traversal order is from small to large
for (int i=2; i<=N; ++i) {
dp[i] = dp[i-1] + dp[i-2];
// Print dp Array , Here slightly
}
return dp[N];
}
}
The results are as follows :

Time complexity and space complexity are O(N), Last , Let's consider state compression , State compression It refers to shrinking dp Size of array , Store only the necessary data , This can further reduce the spatial complexity , In the subject , We can see dp[n] = dp[n-1] + dp[n-2], That is to say, I want to get dp[n], You just need to store dp[n-1] and dp[n-2] These two states are sufficient , That is to say, we can dp The length of the array ranges from N+1 Reduce to 2, In this case, we don't need to use arrays , Just use two variables , The modified code is as follows :
class Solution {
public int fib(int N) {
if (N == 0) {
return 0;
}
// determine dp The initialization state of the array
int prev = 0;
int current = 1;
int sum = 0;
// Loop iteration ,dp Array traversal order is from small to large
for (int i=2; i<=N; ++i) {
sum = prev + current;
prev = current;
current = sum;
}
return current;
}
}
边栏推荐
猜你喜欢

Optimization Practice of Flink OLAP job scheduling and query execution based on ByteDance

Xposed+FDex2 app脱壳 (黑猫投诉app脱壳)

Interviewer: how to deal with the data loss of redis master-slave cluster switching?

视频游戏沉迷行为研究综述

Detail try catch finally

Aike AI frontier promotion (7.27)
详述throw与throws

SparkSubmit.main()方法提交外部参数,远程提交standalone集群任务

详述HashSet的add方法
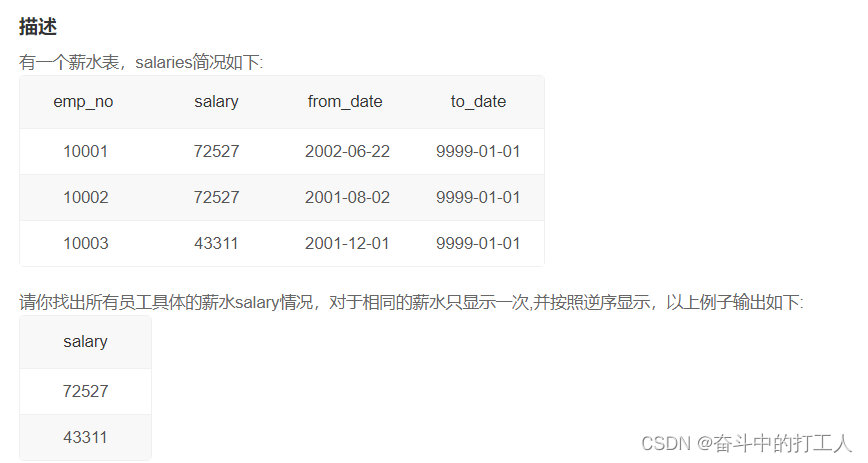
SQL question brushing: find out the current salary of all employees
随机推荐
Map interface
延迟队列DelayQueue性能测试
nodejs body-parser中间件处理类型 multipart/form-data 的 POST 表单数据,req.body无法接收到数据
POJ2446 Chessboard【二分图最大匹配】
What should I do if I can't see any tiles on SAP Fiori launchpad?
Xposed+FDex2 app脱壳 (黑猫投诉app脱壳)
Firefox 103 发布,更快、更安全
(10) STM32 - systick tick timer
Do you really understand CMS garbage collector?
2021-03-15
Self built personalized automatic quotation system to cope with changeable quotation mode
ArrayList常用方法总结
关于2022年3月9日之后Typora登录不了--已解决
Plus SBOM: assembly line BOM pbom
SQL question brushing: find out the current salary of all employees
Poj2594 treasure exploration [bipartite graph minimum path coverage] [Floyd]
Isolation level
Keil mdk5.37 and above can add AC5 (armcc) compiler by themselves
Soft core microprocessor
完美指南|如何使用 ODBC 进行无代理 Oracle 数据库监控?