当前位置:网站首页>[noi Simulation Competition] geiguo and time chicken (structure)
[noi Simulation Competition] geiguo and time chicken (structure)
2022-06-24 08:54:00 【DD(XYX)】
Topic
1s,512mb
Geiguo is a magical country . Because of the good governance given to Taizu ( And found the giving country theorem ), To speed up the development of science and technology , Invented the time chicken . Give Taizu the honor to be the first person to eat time chicken .
At first the chicken would jump to 0 0 0 moment . Then walk normally every time , When they arrive in 2 n + 1 2n+1 2n+1 Caught when . But what makes Taizu unexpected , The timeline of its passage is disrupted by the wormhole . say concretely , i i i Time and j j j Always connected by a wormhole . If time chicken from i − 1 i-1 i−1 here we are i i i moment , It will be immediately transmitted to j j j moment . If time chicken from j − 1 j-1 j−1 here we are j j j moment , It will be immediately transmitted to i i i moment .
All in all n n n Connect two different moments to the wormhole . Every 1 ∼ 2 n 1\sim 2n 1∼2n Is just connected by a wormhole . because 0 0 0 Time and 2 n + 1 2n+1 2n+1 There is no wormhole at all times , It is easy to prove that time chicken can always reach 2 n + 1 2n+1 2n+1 moment . Because of the long time , The wormhole has disappeared , Only the chicken footprints can be seen at any time .
You need to restore a feasible wormhole matching scheme according to the records given to Taizu , Or tell Taizu that the record is wrong .
Input format
The first line has two integers n , m n,m n,m, Indicates that the total time is 2 n + 1 2n+1 2n+1 And the total length of time that footprints exist .
Next line m m m Number , The first i i i Number a i a_i ai Express ( a i , a i + 1 ) (a_i,a_i+1) (ai,ai+1) During this period of time, there are chicken feet .
Output format
If there is no solution output No , Otherwise, output a line first Yes , Then the output n n n That's ok , Two numbers per line x , y x,y x,y , Express ( x , y ) (x,y) (x,y) There is a wormhole between them .
If there are multiple construction schemes , Output any group .
The sample input
3 6
0 1 2 4 5 6
Sample output
Yes
1 5
2 6
3 4
Data range and tips
m ≤ 2 n + 1 , a i − 1 < a i , a 1 = 0 , a m = 2 n m\leq2n+1,a_{i-1}<a_i,a_1=0,a_m=2n m≤2n+1,ai−1<ai,a1=0,am=2n ;
0 ≤ n ≤ 100000 , 0 ≤ m ≤ 200000 0\leq n\leq100000,0\leq m\leq 200000 0≤n≤100000,0≤m≤200000 .
Answer key
We make the number of consecutive segments left in the middle to be A A A , So easy to prove when m − A − 1 m-A-1 m−A−1 There must be no solution when it is an odd number , Because you will match the necessary interval to the non - walkable interval .
Then there are two situations , ( m − A − 1 ) % 4 = 0 (m-A-1)\%4=0 (m−A−1)%4=0 and ( m − A − 1 ) % 4 = 2 (m-A-1)\%4=2 (m−A−1)%4=2 .
The first case can be constructed to prove that there must be a solution :
- First connect the two ends of each non walkable extremely long continuous segment , In this way, there are still m − A − 1 m-A-1 m−A−1 Can match each other .
- Put these matching points on a double ended queue in order .
- Take out the two elements at the beginning of the queue each time A < B A<B A<B , Two elements of the tail of the team C < D C<D C<D .
- matching ( A , C ) , ( B , D ) (A,C),(B,D) (A,C),(B,D) , This will go through ( C , C + 1 ) , ( B , B + 1 ) , (C,C+1),(B,B+1), (C,C+1),(B,B+1), The rest of the queue , ( A , A + 1 ) , ( D , D + 1 ) (A,A+1),(D,D+1) (A,A+1),(D,D+1) .
- Jump back to 3 Step , Until the queue is empty .

In the second case, we find that there may be a solution , If and only if there is such a structure :
The length of the middle section shall be at least 2 Extremely long walkable interval of , The two sides are separated by non walkable sections , about At least one side There is a matching walkable interval .
Take the left as an example , If there is a walkable zone on the left , It is the first red dot on the left in the above figure , Then we can build such a structure :
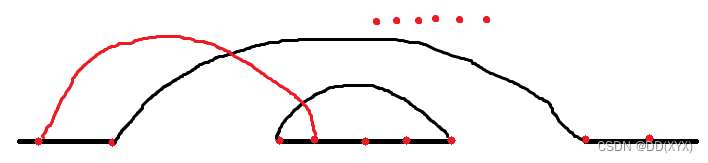
This point matches the first point on the left of the middle section , Two non walkable sections are connected with a large arch bridge at both ends , The remaining matching points are m − A − 3 m-A-3 m−A−3 A the , Can be viewed as % 4 = 0 \%4=0 %4=0 The case structure of . Delete the process through this structure , The rest of the walking is just continuous , Easy to prove correct .
CODE
#include<map>
#include<set>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<random>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_map>
// #pragma GCC optimize(2)
using namespace std;
#define MAXN 200005
#define LL long long
#define ULL unsigned long long
#define ENDL putchar('\n')
#define DB double
#define lowbit(x) (-(x) & (x))
#define FI first
#define SE second
#define PR pair<int,int>
int xchar() {
static const int maxn = 1000000;
static char b[maxn];
static int pos = 0,len = 0;
if(pos == len) pos = 0,len = fread(b,1,maxn,stdin);
if(pos == len) return -1;
return b[pos ++];
}
// #define getchar() xchar()
LL read() {
LL f = 1,x = 0;int s = getchar();
while(s < '0' || s > '9') {
if(s<0)return -1;if(s=='-')f=-f;s = getchar();}
while(s >= '0' && s <= '9') {
x = (x<<1) + (x<<3) + (s^48);s = getchar();}
return f*x;
}
void putpos(LL x) {
if(!x)return ;putpos(x/10);putchar((x%10)^48);}
void putnum(LL x) {
if(!x) {
putchar('0');return ;}
if(x<0) putchar('-'),x = -x;
return putpos(x);
}
void AIput(LL x,int c) {
putnum(x);putchar(c);}
int n,m,s,o,k;
int a[MAXN],ct;
PR b[MAXN];
bool f[MAXN],aa[MAXN];
deque<int> q;
int main() {
freopen("shuttle.in","r",stdin);
freopen("shuttle.out","w",stdout);
n = read(); m = read();
int cn = 0,flg = 0,l = 0,r = 0;
for(int i = 1;i <= m;i ++) {
a[i] = read();
if(i > 1 && a[i] > a[i-1]+1) {
cn ++; aa[a[i]] = 1;
if(cn > 1 && a[i-1] == a[i-2]+1) flg = 1,r = i-1;
}
}
if((m - cn) % 4 == 1) {
for(int i = 2;i <= m;i ++) {
if(a[i] > a[i-1]+1) {
b[++ ct] = {
a[i-1]+1,a[i]};
f[a[i-1]+1] = f[a[i]] = 1;
}
else q.push_back(a[i]);
}
while(!q.empty()) {
int A,B,C,D;
A = q.front(); q.pop_front();
B = q.front(); q.pop_front();
D = q.back(); q.pop_back();
C = q.back(); q.pop_back();
b[++ ct] = {
A,C}; b[++ ct] = {
B,D};
f[A] = f[B] = f[C] = f[D] = 1;
}
int p = 0;
for(int i = 1;i <= (n<<1);i ++) {
if(!f[i]) {
if(p) b[++ ct] = {
p,i},p = 0;
else p = i;
}
}
sort(b + 1,b + 1 + ct);
printf("Yes\n");
for(int i = 1;i <= n;i ++) {
AIput(b[i].FI,' ');
AIput(b[i].SE,'\n');
}
return 0;
}
if((m - cn) % 4 == 3 && flg) {
l = r-1;
while(!aa[a[l]]) l --;
int p1,p2;
p1 = a[l-1]+1; p2 = a[r+1];
b[++ ct] = {
p1,p2}; f[p1] = f[p2] = 1;
p1 = a[l]; p2 = a[r]+1;
b[++ ct] = {
p1,p2}; f[p1] = f[p2] = 1;
int ll = l-1,rr = r+2;
while(aa[a[ll]]) ll --;
while(aa[a[rr]] && rr <= m) rr ++;
if(ll > 1) {
p1 = a[ll]; p2 = a[l+1];
b[++ ct] = {
p1,p2}; f[p1] = f[p2] = 1;
}
else if(rr <= m) {
p1 = a[r]; p2 = a[rr];
b[++ ct] = {
p1,p2}; f[p1] = f[p2] = 1;
}
else return printf("No\n"),0;
for(int i = 2;i <= m;i ++) {
if(a[i] > a[i-1]+1) {
if(i != l && i != r+1) {
b[++ ct] = {
a[i-1]+1,a[i]};
f[a[i-1]+1] = f[a[i]] = 1;
}
}
else if(!f[a[i]]) {
q.push_back(a[i]);
}
}
while(!q.empty()) {
int A,B,C,D;
A = q.front(); q.pop_front();
B = q.front(); q.pop_front();
D = q.back(); q.pop_back();
C = q.back(); q.pop_back();
b[++ ct] = {
A,C}; b[++ ct] = {
B,D};
f[A] = f[B] = f[C] = f[D] = 1;
}
int p = 0;
for(int i = 1;i <= (n<<1);i ++) {
if(!f[i]) {
if(p) b[++ ct] = {
p,i},p = 0;
else p = i;
}
}
sort(b + 1,b + 1 + ct);
printf("Yes\n");
for(int i = 1;i <= n;i ++) {
AIput(b[i].FI,' ');
AIput(b[i].SE,'\n');
}
return 0;
}
printf("No\n");
return 0;
}
边栏推荐
- MyCAT读写分离与MySQL主从同步
- OpenCV每日函数 结构分析和形状描述符(7) 寻找多边形(轮廓)/旋转矩形交集
- Using skills of xargs -- the way to build a dream
- [force deduction 10 days SQL introduction] Day3
- What is SRE? A detailed explanation of SRE operation and maintenance system
- Xiaohei ai4code code baseline nibble 1
- The pie chart with dimension lines can set various parameter options
- K8s deployment of highly available PostgreSQL Cluster -- the road to building a dream
- leetcode 1268. Search suggestions system
- Lombok use
猜你喜欢

【使用 PicGo+腾讯云对象存储COS 作为图床】

数云发布2022美妆行业全域消费者数字化经营白皮书:全域增长破解营销难题
关于 GIN 的路由树

One article explains in detail | those things about growth
![打印出来的对象是[object object],解决方法](/img/fc/9199e26b827a1c6304fcd250f2301e.png)
打印出来的对象是[object object],解决方法

华为路由器:ipsec技术

Pymysql inserts data into MySQL and reports an error for no reason
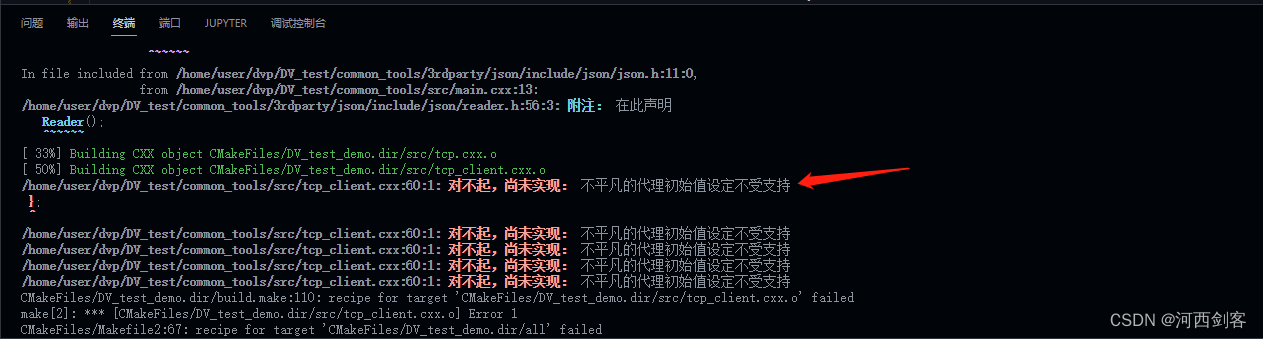
“不平凡的代理初始值设定不受支持”,出现的原因及解决方法
![Jenkins is deployed automatically and cannot connect to the dependent service [solved]](/img/fe/f294955a9bdf7492aab360e44e052d.png)
Jenkins is deployed automatically and cannot connect to the dependent service [solved]

MySQL | view notes on Master Kong MySQL from introduction to advanced
随机推荐
[pytorch basic tutorial 30] code analysis of DSSM twin tower model
“论解不了数独所以选择做个数独游戏这件事”
什么是图神经网络?图神经网络有什么用?
MyCAT读写分离与MySQL主从同步
How does the tunnel mobile inspection track robot monitor 24 hours to ensure the safety of tunnel construction?
用VNC Viewer的方式远程连接无需显示屏的树莓派
The pie chart with dimension lines can set various parameter options
【NOI模拟赛】寄(树形DP)
2022春招面试总结
Qingcloud based R & D cloud solution for geographic information enterprises
基于QingCloud的 “房地一体” 云解决方案
听说你还在花钱从网上买 PPT 模板?
快慢指针系列
[team management] 25 tips for testing team performance management
【团队管理】测试团队绩效管理的25点小建议
【NOI模拟赛】摆(线性代数,杜教筛)
1844. replace all numbers with characters
2022-06-23:给定一个非负数组,任意选择数字,使累加和最大且为7的倍数,返回最大累加和。 n比较大,10的5次方。 来自美团。3.26笔试。
Idea another line shortcut
orb slam build bug: undefined reference to symbol ‘_ ZN5boost6system15system_ categoryEv‘