二分查找

  二分查找也就是折半查找。折半查找是将 N 个元素分成大致相同的两部分。选取中间元素与查找的的元素比较，或者与查找条件相比较，找到或者说找到下一次查找的半区。每次都将范围缩小至 1/2 所以时间复杂度是 O(log₂n），但是二分查找的前提是有序的，一般是从小到排列。
 
 
折半查找的基本思想：
在有序表中（low, high, low<=high），取中间记录即 [(high + low) / 2] 作为比较对象。

• 若给定值与中间记录的关键码相等，则查找成功
• 若给定值小于中间记录的关键码，则在中间记录的左半区继续查找
• 若给定值大于中间记录的关键码，则在中间记录的右半区继续查找

不断重复上述过程，直到查找成功，或所查找的区域无记录，查找失败。
 
 
二分查找的特征：

1. 答案具有单调性；
2. 二分答案的问题往往有固定的问法，比如：令最大值最小（最小值最大），求满足条件的最大（小）值等。

二分查找图解

 
 

二分查找模板

bool check(int x) {
    /* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
// 当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时，其更新操作是r = mid或者l = mid + 1;，计算mid时不需要加1。
int bsearch_1(int l, int r)
{
    
    while (l < r)
    {
    
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
// 当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时，其更新操作是r = mid - 1或者l = mid;，此时为了防止死循环，计算mid时需要加1。
int bsearch_2(int l, int r)
{
    
    while (l < r)
    {
    
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

  在第一段代码中，若 a[mid] ≥ x，则根据序列 a 的单调性，mid 之后的数会更大，所以 ≥ x 的最小的数不可能在 mid 之后，可行区间应该缩小为左半段。因为 mid 也可能是答案，故此时应取 r = mid。同理，若 a[mid] < x，取 l = mid + 1。
  在第二段代码中，若 a[mid] ≤ x，则根据序列 a 的单调性 mid 之前的数会更小，所以 ≤ x 的最大的数不可能在 mid 之前，可行区间应该缩小为右半段。因为 mid 也可能是答案，故此时应取 l = mid。同理，若 a[mid] > x，取 r = mid - 1。

如上面两段代码所示，这种二分写法可能会有两种形式：

1. 缩小范围时，r = mid，l = mid + 1，取中间值时，mid = (l + r) >> 1。
2. 缩小范围时，l = mid，r = mid - 1，取中间值时，mid = (l + r＋1) >> 1。

  如果不对 mid 的取法加以区分，假如第二段代码也采用 mid = (l ＋r) >> 1，那么当 r - l 等于 1 时，就有 mid = (l + r) >> 1 = l。接下来若进入 l = mid 分支，可行区间未缩小，造成死循环；若进入 r = mid - 1 分支，造成 l > r，循环不能以 l = r 结束。因此对两个形式采用配套的 mid 取法是必要的。上面两段代码所示的两个形式共同组成了这种二分的实现方法。注意，我们在二分实现中采用了右移运算 >> 1，而不是整数除法 /2。这是因为右移运算是向下取整，而整数除法是向零取整，在二分值域包含负数时后者不能正常工作。
  仔细分析这两种 mid 的取法，我们还发现：mid = (l + r) >> 1 不会取到 r 这个值，mid = (l + r＋1) >> 1不会取到l这个值。我们可以利用这一性质来处理无解的情况，把最初的二分区间 [1, n] 分别扩大为 [1, n+1] 和 [0, n]，把 a 数组的一个越界的下标包含进来。如果最后二分终止于扩大后的这个越界下标上，则说明 α 中不存在所求的数。

  
总而言之，正确写出这种二分的流程是：

1. 通过分析具体问题，确定左右半段哪一个是可行区间，以及 mid 归属哪一半段。
2. 根据分析结果,选择“r = mid, l = mid + 1, mid = (l＋r) >> 1”和“l = mid，r = mid - 1，mid = (l＋r＋1) >> 1”两个配套形式之一。
3. 二分终止条件是 l == r，该值就是答案所在位置。

  也有其他的二分写法，采用“l = mid + 1, r = mid-1”或“l = mid, r = mid”来避免产生两种形式，但也相应地造成了丢失在 mid 点上的答案二分结束时可行区间未缩小到确切答案等问题，需要额外加以处理。
  C++ STL 中的 lower_bound 与upper_bound 函数实现了在一个序列中二分查找某个整数x 的后继。

 
 

精度模板：

//模版一：实数域二分，设置eps法

//令 eps 为小于题目精度一个数即可。比如题目说保留4位小数，0.0001 这种的。那么 eps 就可以设置为五位小数的任意一个数 0.00001- 0.00009 等等都可以。

//一般为了保证精度我们选取精度/100 的那个小数，即设置 eps= 0.0001/100 =1e-6

while (l + eps < r)
{
    
    double mid = (l + r) / 2;

    if (pd(mid))
        r = mid;
    else
        l = mid;
}

//模版二：实数域二分，规定循环次数法

//通过循环一定次数达到精度要求，这个一般 log2N < 精度即可。N 为循环次数，在不超过时间复杂度的情况下，可以选择给 N 乘一个系数使得精度更高。

    for (int i = 0; i < 100; i++)
{
    

    double mid = (l + r) / 2;
    if (pd(mid))
        r = mid;
    else
        l = mid;
}

 
 

 
 

 
 

题目

分巧克力

题目链接

解题思路：
简单思路，边长的最大规模为 100000；我们可以枚举出所有的情况。按从大到小的顺序进行切割，直到找到满足要求的巧克力边长。

在判断边长是否满足条件时：求一块长方形（h * w）最多被分成的正方形（len * len）巧克力个数为：

cnt = (h / len) \* (w / len)

但是使用朴素算法枚举时间复杂度 O(n)*O(n) =O(n²) 会超时，所以改用 2 分查找法，这找到符合要求的最大的一个。

即用在单调递增序列 a 中查找 <=x 的数中最大的一个（即 x 或 x 的前驱）即可，原本这里的条件是 <=x ，我们将其换成验证即可。

 
 

#include <iostream>
using namespace std;
int N, K, H[100010], W[100010];

bool judge(int k){
    //判断长度k是否符合条件 
  int sum = 0;
  for(int i = 0; i < N; i ++){
    
    sum += (H[i] / k) * (W[i] / k);
    if(sum >= K)//到达要求后直接返回 
      return true;//符合 
  }
  return false;//不符合 
}

int main()
{
    
  // 请在此输入您的代码
  scanf("%d %d", &N, &K);
  for(int i = 0; i < N; i ++)
    scanf("%d %d", &H[i], &W[i]);
  
  int l = 1, r = 100001;
  while(l <= r){
    //二分查找 
    int mid = (l + r) / 2;
    if(judge(mid))
      l = mid + 1;
    else
      r = mid - 1;
  }
  printf("%d", r);
  return 0;
}

 
 

 
 

M 次方根

题目链接

 
 
题目分析：
这题涉及到了精度，我们使用精度版本。
下面我们设计 pd 函数：pd 成功的情况，一定是 pd 的 mid 符合条件，且小于 mid 的一定符合条件。因此我们要在大于 mid 中继续查找，找到更大的 mid。

double pd(double a,int m)
{
    
    double c = 1;
    while(m > 0)
    {
    
        c = c * a;
        m --;
    }
    if(c >= n)
        return true;
    else
        return false;
}

 
 

#include <cstdio>
#include <iostream>
using namespace std;

double n,l,r,mid;
double eps = 1e-8;

bool pd(double a, int m){
    
    double c = 1;
    while(m > 0){
    
        c = c * a;
        m --;
    }
    if(c >= n)
        return true;
    else
        return false;
}

int main(){
    
    int m;
    cin>>n>>m;

	//设置二分边界
    l = 0, r = n;

	//实数二分
    while (l + eps < r){
    
        double mid = (l + r) / 2;
        if (pd(mid, m))
            r = mid;
        else
            l = mid;
    }

    printf("%.7f", l);
    return 0;
}

 
 

 
 

数字在排序数组中出现的次数

题目链接

时间复杂度：O(logn)

class Solution {
    
public:
    int getNumberOfK(vector<int>& nums , int k) {
    
        if(!nums.size())
            return 0;
        
        int l1 = 0, r1 = nums.size() - 1;
        while(l1 < r1){
    
            int mid = l1 + r1 >> 1;
            if(nums[mid] >= k)
                r1 = mid;
            else
                l1 = mid + 1;
        }
        
        int l2 = 0, r2 = nums.size() - 1;
        while(l2 < r2){
    
            int mid = l2 + r2 + 1 >> 1;
            if(nums[mid] <= k)
                l2 = mid;
            else
                r2 = mid - 1;
        }
        
        if(nums[l1] != k && nums[l2] != k)
            return 0;
        return l2 - l1 + 1;
    }
};

使用lower_bound和upper_bound函数。

class Solution {
    
public:
    int getNumberOfK(vector<int>& nums , int k) {
    
        auto l = lower_bound(nums.begin(), nums.end(), k);
        auto r = upper_bound(nums.begin(), nums.end(), k);

        return r - l;
    }
};

 
 

 
 

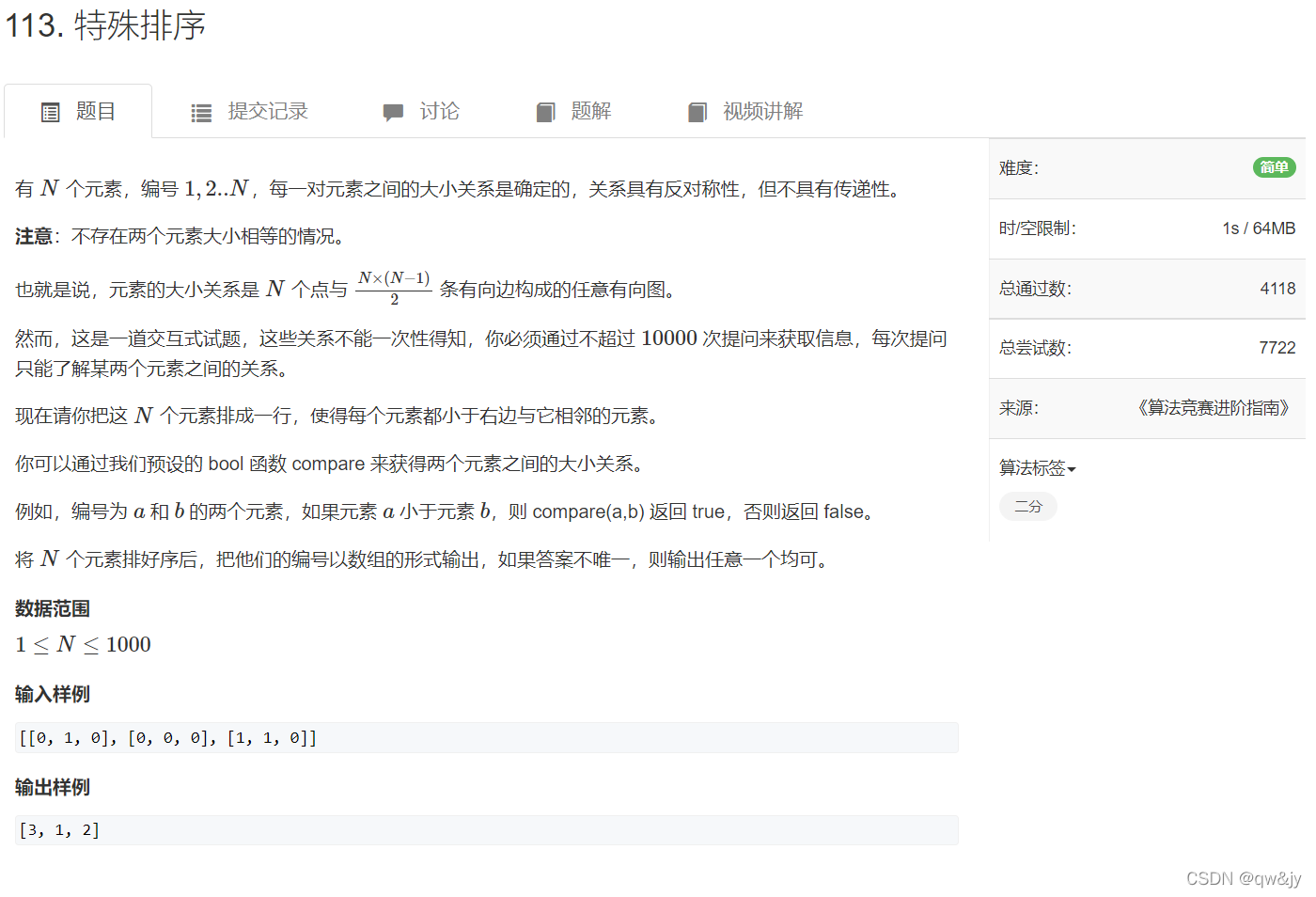
特殊排序

题目链接

样例：
指的是对于3个数的每组compare
compare（1，1）=0
compare（1，2）=1
compare（1，3）=0
compare（2，1）=0
compare（2，2）=0
compare（2，3）=0
compare（3，1）=1
compare（3，2）=1
compare（3，3）=0

首先假设 vector 中有排好序的一组元素：a, b, c, d, e
现在我们要在 vector 中插入f，如何确定 f 的位置？直接二分 mid = c，如果 f > c 那么 f 在 c，e 之间，反之在 a，c 之间。(通过二分查找找到插入的位置)

// Forward declaration of compare API.
// bool compare(int a, int b);
// return bool means whether a is less than b.

class Solution {
    
public:
    vector<int> specialSort(int N) {
    
        vector<int> res;
        res.push_back(1);
        for(int i = 2; i <= N; i ++){
    
            int l = 0, r = res.size() - 1;
            while(l <= r){
    
                int mid = l + r >> 1;
                if(compare(res[mid], i))
                    l = mid + 1;
                else
                    r = mid - 1;
            }
            res.push_back(i);
            for(int j = res.size() - 2; j > r; j --)//选择插入
                swap(res[j], res[j + 1]);
        }
        return res;
    }
};

 
 

 
 

不修改数组找出重复的数字

题目链接

分治+抽屉原理：一共有 n+1 个数，每个数的取值范围是1到n，所以至少会有一个数出现两次。

分治的思想，将每个数的取值的区间 [1, n] 划分成 [1, n / 2] 和 [n / 2 + 1, n] 两个子区间，然后分别统计两个区间中数的个数。
注意这里的区间是指 数的取值范围，而不是 数组下标。

划分之后，左右两个区间里一定至少存在一个区间，区间中数的个数大于区间长度。
这个可以用反证法来说明：如果两个区间中数的个数都小于等于区间长度，那么整个区间中数的个数就小于等于n，和有n+1个数矛盾。

因此我们可以把问题划归到左右两个子区间中的一个，而且由于区间中数的个数大于区间长度，根据抽屉原理，在这个子区间中一定存在某个数出现了两次。

依次类推，每次我们可以把区间长度缩小一半，直到区间长度为1时，我们就找到了答案。

class Solution {
    
public:
    int duplicateInArray(vector<int>& nums) {
    
        int l = 1, r = nums.size() - 1;
        while(l < r){
    
            int mid = l + r >> 1;//区间划分[l, mid], [mid + 1, r]
            int s= 0;
            for(int i = 0; i < nums.size(); i++)//统计数组中位于左半区间的数的个数[l ,mid]
                if(l <= nums[i] && nums[i] <= mid)
                    s ++;
            if(s > mid - l + 1)
                r = mid;
            else
                l = mid + 1;
        }
        return r;
    }
};