The concept and properties of mba-day26 number

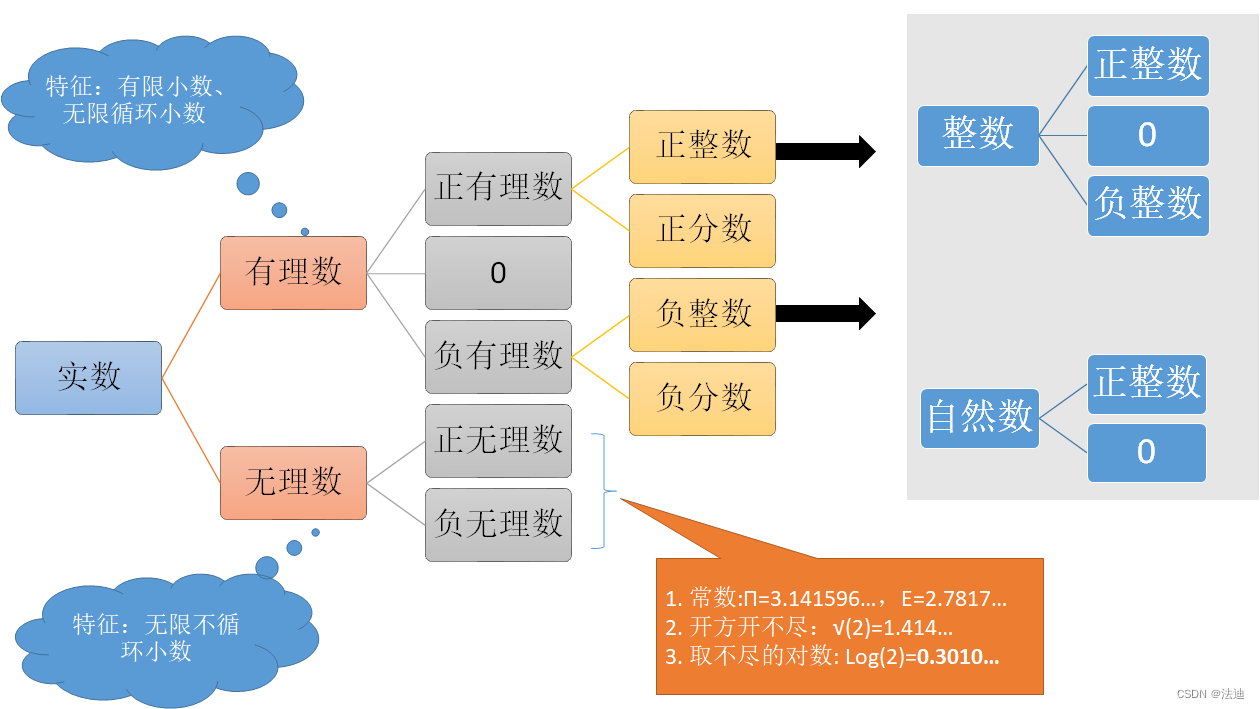
1. common ： The set of real Numbers 、 Rational number 、 Irrational number 、 Integers 、 The concept of natural numbers

• The set of real Numbers ： There are rational numbers and irrational numbers （ Infinite non recurring decimals ）
• Rational number ： Positive rational numbers ,0, Negative rational numbers
• Irrational number ： Positive irrational number , Negative irrational numbers （ constant 1. constant :Π=3.141596…,E=2.7817…2. There is no end to prescribing ：√(2)=1.414…3. Take infinite logarithms :Log(2)=0.3010…）
• Integers ： Positive integer ,0, Negtive integer
• Natural number ：0, Positive integer

2. Prime and sum

1. Prime number ： Only disassemble 1 And its own 2 A positive integer with a divisor , for example 7,11
2. Sum ： except 1 And a positive integer that has other divisors , for example 9,12
3. Prime and composite numbers have the following important properties

1. 20 The prime number within ：2,3,5,7,11,13,17,19
2. 2  Is a unique even prime number , Other prime numbers are odd numbers ( Except for the minimum prime number 2 It's even , Other prime numbers are odd numbers )
3.  The minimum prime number is 2
4.  Any composite number can be decomposed into prime numbers and multiplied . for example 8=2*2*2

4. Reciprocal number
5. The common divisor is 1 The two numbers of are called coprime numbers , for example 9 and 16

3. Odd and even numbers

1. Odd number ： Can not be 2 Divisible number
2. even numbers ： Can be 2 Divisible number , among 0 It's even
   Integers Z = Odd number and even numbers = 2n+1 and 2n

Be careful ： Two adjacent integers must be odd and even , Except for the minimum prime number 2 It's even , Other prime numbers are odd numbers

3. nature
   Both are even numbers , Different to odd

 Odd number  +  Odd number  =  even numbers 
 even numbers  +  even numbers  =  even numbers 
 Odd number  +  even numbers  =  Odd number 

4. Examination site

【】+【】= Odd number , Then it must be   An odd number an even number 
【】+【】+【】= Odd number , Then all are odd numbers , or   Two even numbers and one odd number 
【】+【】+【】= even numbers , Then all are even numbers , or   Two odd numbers and one even number 
 Prime number + Prime number = Prime number , Then there will be 2
 Prime number * Prime number = even numbers , Then there will be 2

4. to be divisible by 、 Multiple 、 Divisor

1. Division of numbers
2. greatest common divisor , for example (8, 12, 24) The approximate number is （2, 4）, The greatest common divisor is 4
3. Minimum common multiple , for example [8, 12, 24, 48], The multiple is (48,96…), The least common multiple 48
4. Finding the least common multiple

 for example [12, 15]
   3 |12, 15
      -------
       4  5
 Minimum common multiple ：3*4*5 = 60

a * b = [a, b]*(a, b) =  Minimum common multiple * greatest common divisor  = 60 * 3

5. Decomposing the prime factor
   seek [8,27,36,35] The least common multiple of

 The same factor is the most , Multiply by the unique factor 

8=2*2*2*2
27=3*3*3
36=2*2*3*3
35=5*7

[8,27,36,35]=2*2*2*2 * 3*3*3 * 5*7

6. A common characteristic of divisibility

• Can be 2 Divisible number ： Bits are even 0,2,4,6,8
• Can be 3 Divisible number ： The sum of the digits must be 3 to be divisible by
• Can be 9 Divisible number ： The sum of digits must be 9 to be divisible by
• Can be 5 Divisible number ： One digit 0 or 5
• Can be 6 Divisible number ： At the same time, satisfaction can be 2 and 3 The condition of division , Or can be 3 Even number of integral division
• Can be 10 Divisible number ： A bit must be 0
• Can be 11 Divisible number ： From right to left , The sum of odd digits minus the sum of even digits can be 11 to be divisible by （ Include 0）

 for example ：
3949 -> [(9+9) - (3+4) ]/ 11 = 1, That is, satisfaction can be 11 Divisible number 
286 -> [(2+6) - 8] / 11 = 0, That is, satisfaction can be 11 Divisible number