当前位置:网站首页>面试考点:三种图的问题
面试考点:三种图的问题
2022-07-27 12:48:00 【&永恒的星河&】
拓扑排序
在图论中,拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。且该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次。
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
有向无环图(DAG)才有拓扑排序,非DAG图没有拓扑排序一说。
拓扑排序通常用来“排序”具有依赖关系的任务。
Python实现
# 输入top排序的任意一条路径,用来判断有向图是否有环
def topSort(n, path):
"""
DAG图的拓扑排序
n:节点个数
path: 图中边
"""
# 统计每个节点的出度节点是谁
graph = {}
# 统计每个节点的入度数
in_dgree = {i:0 for i in range(n)}
for i, j in path:
if i in graph:
graph[i].append(j)
else:
graph[i] = [j]
in_dgree[j] += 1
# 设置栈用来存储入度为0的节点
stack = []
# 用来保存top排序的结果
res = []
# 将入度为0的节点压入栈
for t in in_dgree:
if in_dgree[t] == 0:
stack.append(t)
# 出入栈实现节点入度和出度
while stack:
m = stack.pop()
res.append(m)
if m in graph:
for k in graph[m]:
in_dgree[k] -= 1
if in_dgree[k] == 0:
stack.append(k)
if len(res) == n:
return res
return []
path = [(0,3), (0,1), (1,3), (1,2), (2,4), (3,2), (3,4)]
n = 5
rt = topSort(n, path)
print(rt)单源节点最短路径
介绍: 算法:利用Dijkstra算法求解从北京到海南最短路径_&永恒的星河&的博客-CSDN博客
python实现
def shortestPath(path, n):
"""
path: (start, end, weight)
n: 节点的个数
"""
# 存放从源节点到其他节点的最短路径和当下所属父亲节点(parent, distance)
dst = [(-1, float("inf")) for _ in range(n)]
# 设置节点是否被访问过
visited = [False for _ in range(n)]
# 使用邻接矩阵对图进行存储
graph = [[float("inf") for _ in range(n)] for _ in range(n)]
for i, j, w in path:
graph[i][j] = w
# 用来保存每个节点的父亲节点
parent = [-1 for _ in range(n)]
# 计算源节点到其他节点的最短路径
for i in range(1, n):
if graph[0][i] != float("inf"):
dst[i] = (0, graph[0][i])
visited[0] = True
# 求解最短路径
for _ in range(n):
middle = -1
mindst = float("inf")
cur_parent = -1
# 求解dst中最小距离
for i in range(n):
if not visited[i] and dst[i][1] != float("inf"):
if dst[i][1] < mindst:
mindst = dst[i][1]
middle = i
cur_parent = dst[i][0]
if cur_parent != -1:
visited[middle] = True
parent[middle] = cur_parent
# 更新dst中距离
for i in range(n):
if not visited[i] and graph[middle][i] != float("inf"):
if dst[middle][1] + graph[middle][i] < dst[i][1]:
dst[i] = (middle, dst[middle][1] + graph[middle][i])
# 进行回溯
for i in range(1, n):
k = i
path = [k]
while parent[k] != -1:
path.insert(0, parent[k])
k = parent[k]
print("path:{}, dst={}".format(path, dst[i][1]))
# 0-1-3
# 0-2-3
# 1-2
path = [(0,1,2),(0,2,1),(2,3,6),(1,3,4),(1,2,4)]
n = 4
shortestPath(path, n)图的深度优先遍历

python实现
def graphDFSTravel(path, n, start_node):
"""
图的深度优先遍历算法(采用邻接矩阵进行存储)
path: 存储图的图中边
n: 节点的个数
start_node: 开始节点
"""
visited = [False for _ in range(n)]
res = []
# 使用邻接矩阵存储图
graph = [[float("inf") for _ in range(n)] for _ in range(n)]
for i, j in path:
graph[i][j] = 1
graph[j][i] = 1
# 存储遍历结果
res = []
# 深度优先遍历节点
def dfs(i):
if i >= 0 and i < n and not visited[i]:
res.append(i)
visited[i] = True
for k in range(n):
if float(graph[i][k]) != float('inf'):
dfs(k)
dfs(start_node)
return res
path = [(0,1),(0,4),(1,3),(0,2)]
n = 5
res = graphDFSTravel(path, n, 0)
print(res)边栏推荐
猜你喜欢

【萌新解题】斐波那契数列
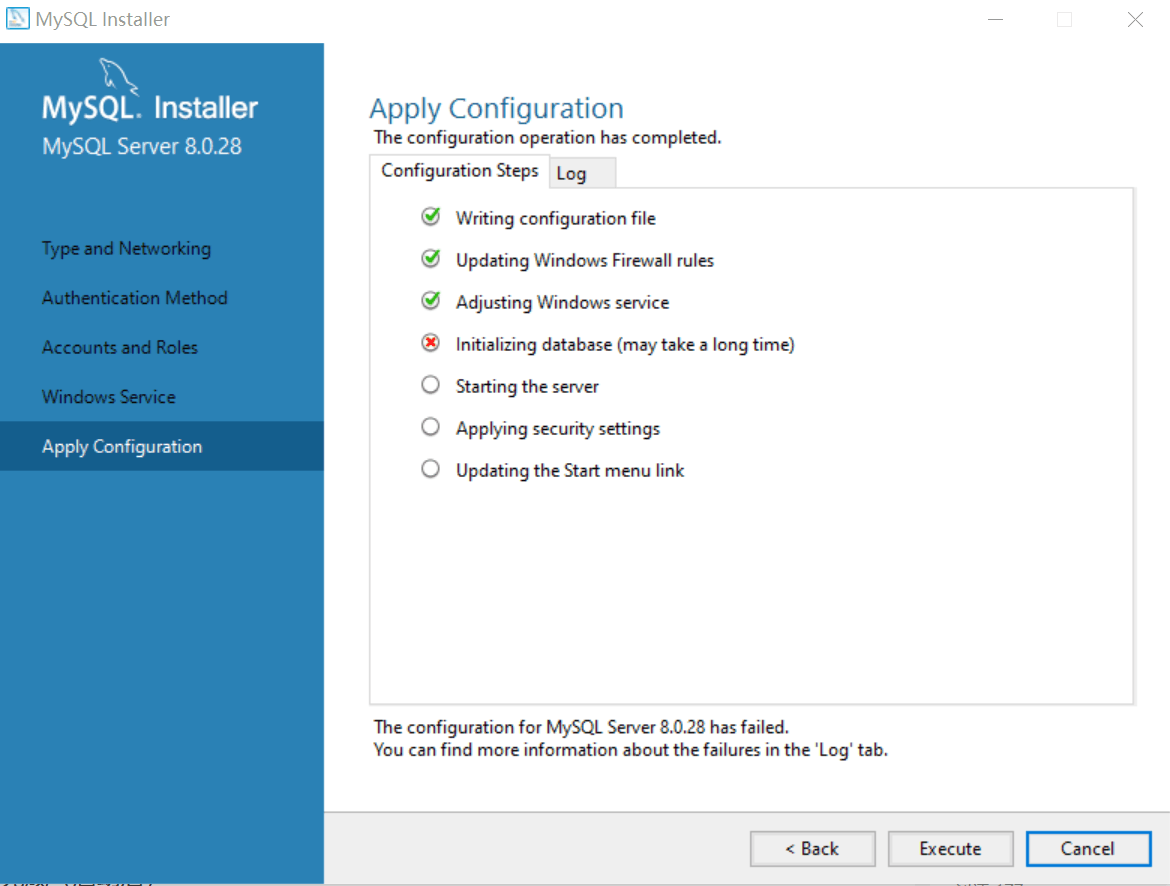
Initializing database error after reinstalling MySQL

@Simple use of conditional

BSP video tutorial issue 21: easy one key implementation of serial port DMA variable length transceiver, support bare metal and RTOS, including MDK and IAR, which is more convenient than stm32cubemx (

Is it easy to find a job after programmer training and learning

分布式系统架构理论与组件

JS true / false array conversion

AMD Adrenalin 22.7.1 驱动更新:OpenGL 性能翻倍,支持微软 Win11 22H2 系统

Overview of static inner classes and non static inner classes

开源项目丨Taier1.2版本发布,新增工作流、租户绑定简化等多项功能
随机推荐
sql 语句问题, 求计算相差10分钟以内的数据作为同一批次数据显示
PG synchronizes multiple data tables to MySQL. Is there a way to simplify the configuration?
CEPH distributed storage performance tuning (6)
500强企业如何提升研发效能?来看看行业专家怎么说!
Interviewer: how to deal with the data loss of redis master-slave cluster switching?
v-on基础指令
PySide6/PyQt开发经验总结(2) - 设置快捷键
BSP视频教程第21期:轻松一键实现串口DMA不定长收发,支持裸机和RTOS,含MDK和IAR两种玩法,比STM32CubeMX还方便(2022-07-24)
初学者入门:使用WordPress搭建一个专属自己的博客
文本样式
程序员培训学习后好找工作吗
About typora's inability to log in after March 9, 2022 -- resolved
Seata 在蚂蚁国际银行业务的落地实践
Background and framework introduction and basic environment preparation of hucang integrated e-commerce project
Map interface
Minimally invasive brain science broke the listing: the company's market value is HK $14.3 billion, and minimally invasive medical is the major shareholder
固定定位
Connotative quotations
Overview of famous inner classes and anonymous inner classes
Multi activity disaster recovery construction after 713 failure of station B | takintalks share