当前位置:网站首页>Paper notes: knowledge map kgat (unfinished temporary storage)
Paper notes: knowledge map kgat (unfinished temporary storage)
2022-07-26 09:18:00 【Min fan】
Abstract : Share your understanding of the paper . See the original X. Wang et al., KGAT: Knowledge Graph Attention Network for Recommendation, KDD 2019.
0. Contribution of thesis
- In the collaborative knowledge map (Collaborative knowledge graph) Modeling high-order relationships is shown in , Use project information for better recommendation system modeling .
- Propose a new method KGAT, Provide a high-order model under the framework of graph neural network .
- Fast and good .
- Provide code : https://github.com/xiangwang1223/knowledge_graph_attention_network.
1. Basic ideas

user And user, user And item The relationship between has certain transitivity . The number of passes is the corresponding order (order). order = 3 when , u 1 u_1 u1 And i 3 i_3 i3 and i 4 i_4 i4 Link ; order = 4 when , u 1 u_1 u1 And u 2 , u 3 u_2, u_3 u2,u3 Link .
2. Problem modeling
| Symbol | meaning | remarks |
|---|---|---|
| U \mathcal{U} U | User set | |
| I \mathcal{I} I | Project collection | |
| G 1 \mathcal{G}_1 G1 | user - The second part of the project | G 1 ⊆ U × I \mathcal{G}_1 \subseteq \mathcal{U} \times \mathcal{I} G1⊆U×I, It can be considered as a directed graph |
| E \mathcal{E} E | Set of entities | It can be a user or a project |
| R \mathcal{R} R | Relational sets | |
| G 2 \mathcal{G}_2 G2 | Knowledge map | G 2 ⊆ E × R × E \mathcal{G}_2 \subseteq \mathcal{E} \times \mathcal{R} \times \mathcal{E} G2⊆E×R×E, It's a digraph |
| A \mathcal{A} A | Project entity alignment | A ⊂ I × E \mathcal{A} \subset \mathcal{I} \times \mathcal{E} A⊂I×E |
| G \mathcal{G} G | Unified knowledge map | G ⊆ E ′ × R ′ × E ′ \mathcal{G} \subseteq \mathcal{E}' \times \mathcal{R}' \times \mathcal{E}' G⊆E′×R′×E′ |
| E ′ \mathcal{E}' E′ | All entities | E ′ = E ∪ U \mathcal{E}' = \mathcal{E} \cup \mathcal{U} E′=E∪U, Include users 、 project 、 Project properties |
| − r -r −r | The reverse of the relationship | The movie By Starring actors |
user - The second part of the project .
{ ( u , y u i , i ) ∣ u ∈ U , i ∈ I } \{(u, y_{ui}, i) \vert u \in \mathcal{U}, i \in \mathcal{I}\} {(u,yui,i)∣u∈U,i∈I}, y u i = 1 y_{ui} = 1 yui=1 Indicates that the user is associated with the project ( Watching the film 、 Bought goods ).
Make complaints : People who engage in machine learning can write this model , Obviously, it is a common figure , No need at all y u i y_{ui} yui.Project knowledge map
{ ( h , r , t ) ∣ h , t ∈ E , r ∈ R ) } \{(h, r, t) \vert h, t \in \mathcal{E}, r \in \mathcal{R})\} {(h,r,t)∣h,t∈E,r∈R)}.Project entity alignment
A = { ( i , e ) ∣ i ∈ I , e ∈ E } \mathcal{A} = \{(i, e) \vert i \in \mathcal{I}, e \in \mathcal{E}\} A={(i,e)∣i∈I,e∈E} Mistake . Actually A \mathcal{A} A Is a subset of the latter .Problem description
Input : Collaborative knowledge map G \mathcal{G} G;
Output : y ^ u i \hat{y}_{ui} y^ui, The user u u u And projects i i i Related ( like , Want to buy ) The possibility of .
3. Method
The embedded (embedding) Learning a vector for each entity , Used to indicate it .
After embedding , You can use the distance between vectors to calculate the similarity of entities ( Relevance ).
4. doubt
- It is clearly a three part graph ( user 、 project 、 attribute ), Why do we have to make a bipartite picture of users and projects , And make items and attributes into a knowledge map ?
边栏推荐
猜你喜欢
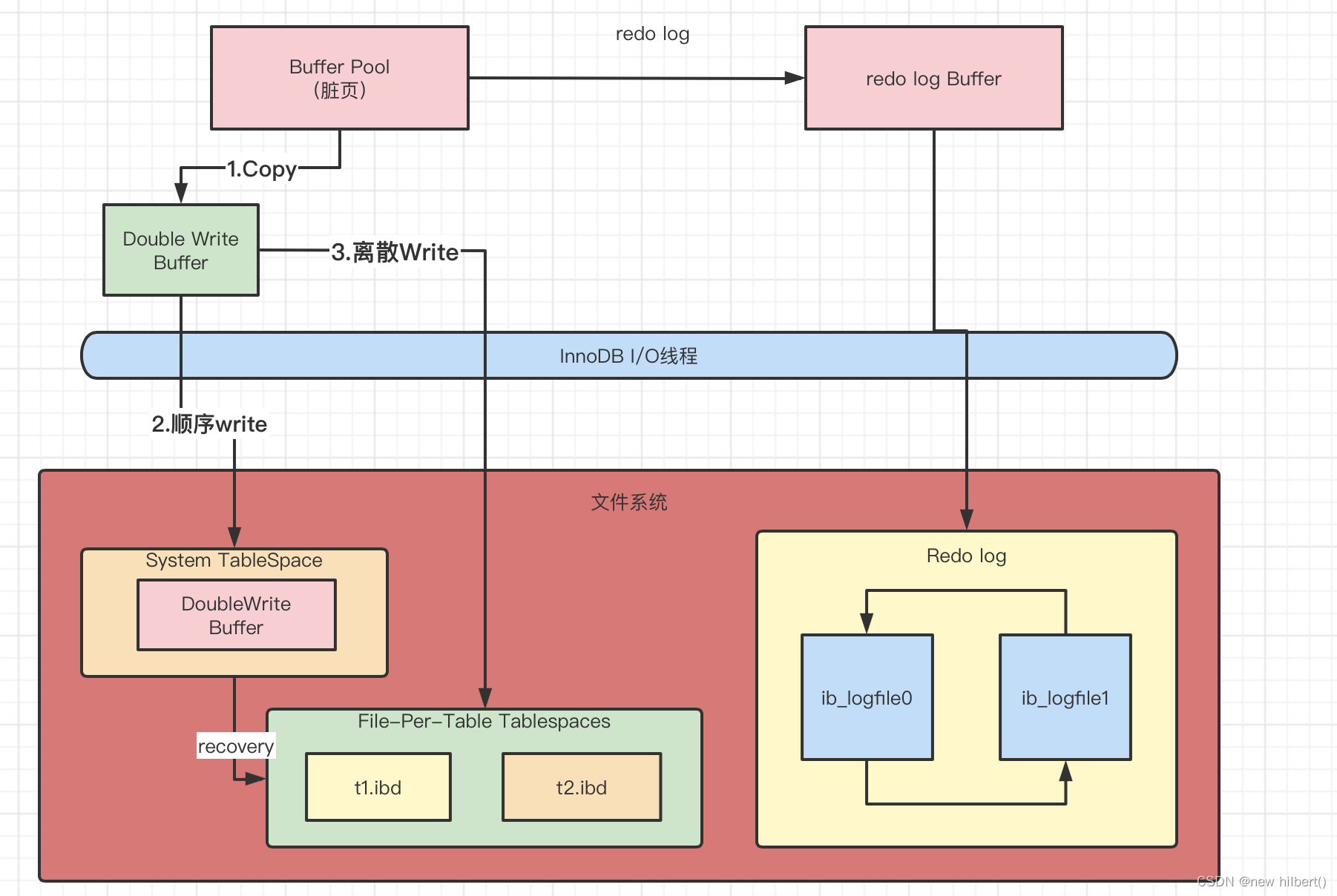
【Mysql】一条SQL语句是怎么执行的(二)

QtCreator报错:You need to set an executable in the custom run configuration.

Use of off heap memory

Datawhale panda book has been published!

volatile 靠的是MESI协议解决可见性问题?(上)
2022茶艺师(中级)特种作业证考试题库模拟考试平台操作

Flask project learning (I) -- sayhello
2022流动式起重机司机考试题模拟考试题库模拟考试平台操作
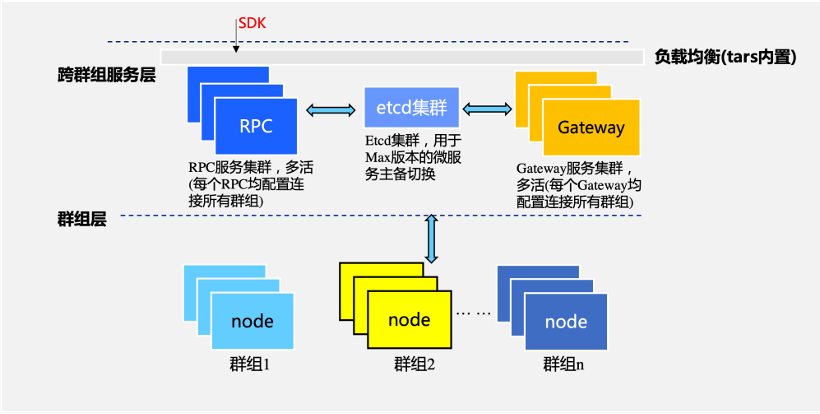
公告 | FISCO BCOS v3.0-rc4发布,新增Max版,可支撑海量交易上链
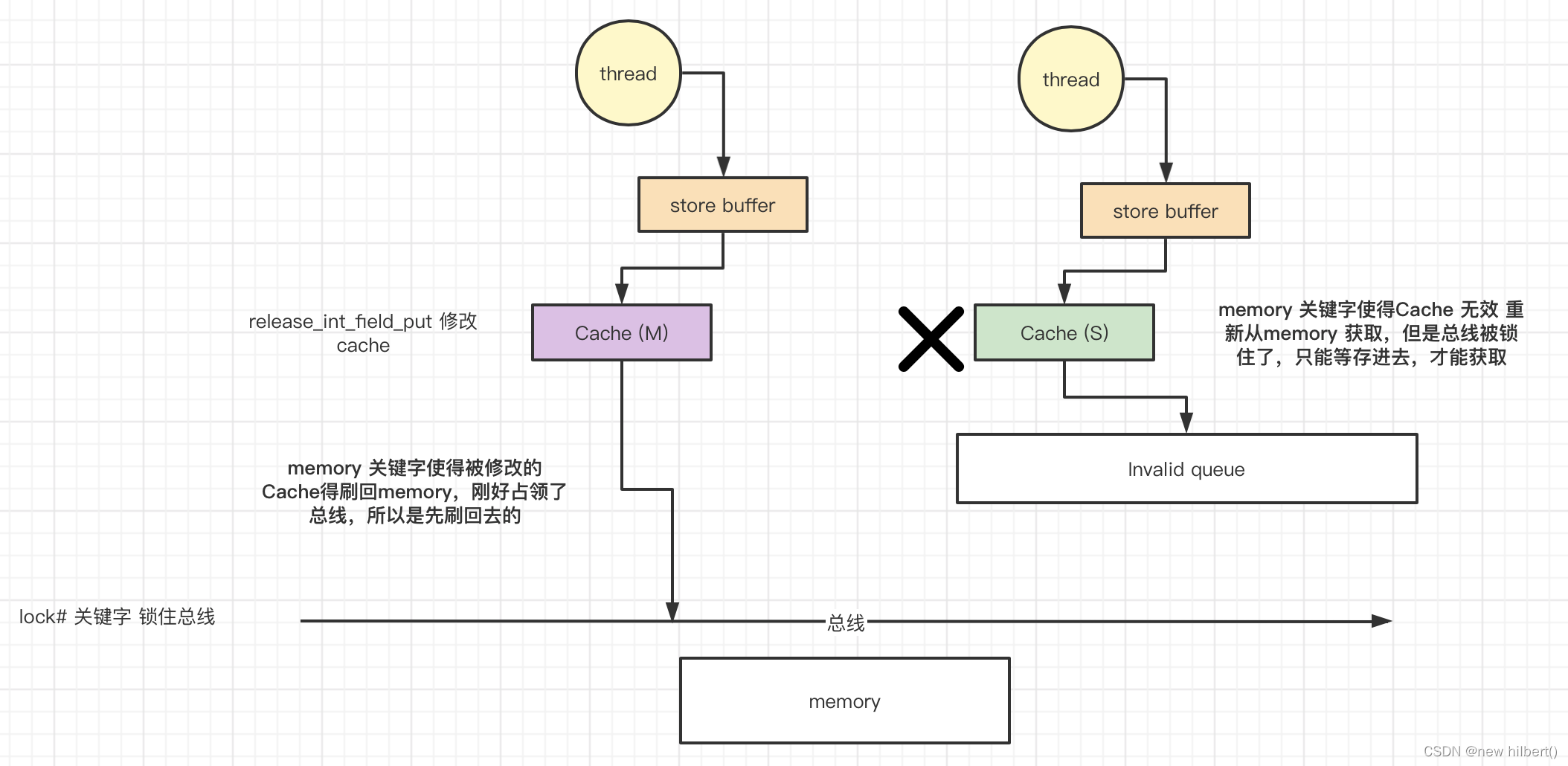
Does volatile rely on the MESI protocol to solve the visibility problem? (next)
随机推荐
Stm32+mfrc522 completes IC card number reading, password modification, data reading and writing
PAT 甲级 A1034 Head of a Gang
李沐d2l(四)---Softmax回归
Where are the laravel framework log files stored? How to use it?
原根与NTT 五千字详解
网络安全漫山遍野的高大上名词之后的攻防策略本质
【线上死锁分析】由index_merge引发的死锁事件
STM32+MFRC522完成IC卡号读取、密码修改、数据读写
深度学习常用激活函数总结
谷粒学院的全部学习源码
Li Mu D2L (IV) -- softmax regression
Apple generated and verified tokens for PHP
Simple message mechanism of unity
Nuxt - Project packaging deployment and online to server process (SSR server rendering)
codeforces dp合集
李沐d2l(五)---多层感知机
unity简易消息机制
Error: Cannot find module ‘umi‘ 问题处理
Use of off heap memory
Grain College of all learning source code